14. パッシブフィルタ回路
パッシブフィルターは、抵抗(\(R\))、コイル(\(L\))、およびコンデンサ(\(C\))などのパッシブな電子部品(これらを受動素子といい、電源を必要としない素子である)を使用して信号をフィルタリングするデバイスである。これらの素子は電気的な特性に基づいて信号の周波数成分を選択することができ、主にアナログ信号の処理に使用される。パッシブフィルターは、周波数特性によって、主に以下の3つの種類に分けられる。
・ローパスフィルター(Low-Pass Filter):低周波の信号を通過させ、高周波の信号を減衰させるフィルター。
・ハイパスフィルター(High-Pass Filter):高周波の信号を通過させ、低周波の信号を減衰させるフィルター。
・バンドパスフィルター(Band-Pass Filter):特定の周波数帯の信号を通過させ、それ以外の周波数の信号を減衰させるフィルター。
パッシブフィルターは、幅広い用途で使用されている重要な回路である。
パッシブフィルターの主な用途:
・オーディオ機器:音声信号の周波数特性を調整するために使用。
・無線機器:不要な周波数の信号を除去するために使用。
・電源回路:出力電圧の平滑化やノイズの除去のために使用。
パッシブフィルターの利点(アクティブフィルターとの比較において):
・安定性が保証されている。
・能動素子では困難な大きな信号を取り扱うことができる。(数10 A、数百100 Vの信号が扱える)
・高周波動作が可能である。(UHF以上の周波数帯域での使用が可能)
・電力を消費しない。(ただし、信号が通過する際の電力は消費する)
パッシブフィルターの欠点:
・周波数特性が限定的である。
・設計が難しい。
・部品点数が多い。
以下の説明で使う、インピーダンスについては、「29. インピーダンスとアドミタンス」を参照してください。
また、伝達関数に関連した事項は、「9.伝達関数」及び、「18.システムの周波数応答」を参照してください。
ローパスフィルター(Low-Pass Filter:LPF)
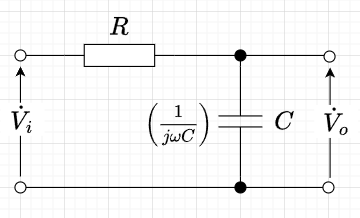
図1は、「R-C 1次LPFの回路図」である。\(R,\;C\)に流れる電流を\(\dot{I}\)とすると、図より、次の式が成り立つ。$$\dot{V}_i=\left( R + \frac{1}{j \omega C}\right) \dot{I} \\ \dot{V}_o = \frac{1}{j \omega C} \dot{I}$$ この2式より、$$\dot{V}_o = \left(\frac{\frac{1}{j \omega C}}{R+\frac{1}{j \omega C}}\right) \dot{V}_i \\ = \frac{1}{1 + j \omega C R} \dot{V}_i$$となる。また、$$A(j \omega) = \frac{ \dot{V}_o}{\dot{V}_i} = \frac{1}{1 + j \omega CR}$$とし、これを伝達関数という。
振幅特性\(|A(j\omega)|\)は$$|A(j \omega)| = \frac{1}{\sqrt{1 +(\omega C R)^2}}$$であり、位相特性\(arg[A(j \omega)]\)は、$$arg[A(j \omega)] = - \tan^{-1} \omega C R$$である。
振幅特性の式より、振幅が\(1/\sqrt{2}\)(\(-3dB\))になる角周波数(遮断周波数)は\(\omega_C=\frac{1}{CR}\) [rad/s](周波数\(f_C=\frac{1}{2\pi CR}\) [Hz])である。また、位相は\(-45\;\)度となる。なお、\(\tau =CR\) [s]を時定数という。
※\(dB\)(デシベル)については、「19. ボード線図」を、また、時定数については「13. 一次遅れ要素(1次遅れ系)の時間応答」を参照してください。
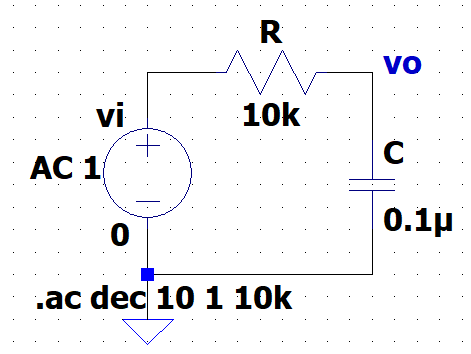
図2「R-C1次LPF(LTspice)」は、AC解析(周波数特性)用のLTspice回路図である。抵抗\(R : \;10\;k\Omega\)、コンデンサ\(C:\;0.1\;\mu F\)と設定している。従って、遮断周波数は、$$f_C = \frac{1}{2\pi CR} \approx 159 \; [Hz]$$である。
図3がLTspiceによる解析結果の「R-C1次LPFの周波数特性」で、赤線の実線が振幅特性、破線が位相特性である。遮断周波数\(f_c:159\;Hz\)において、振幅は\(-3\;dB\)、位相は\(-45\;\)度となっている。
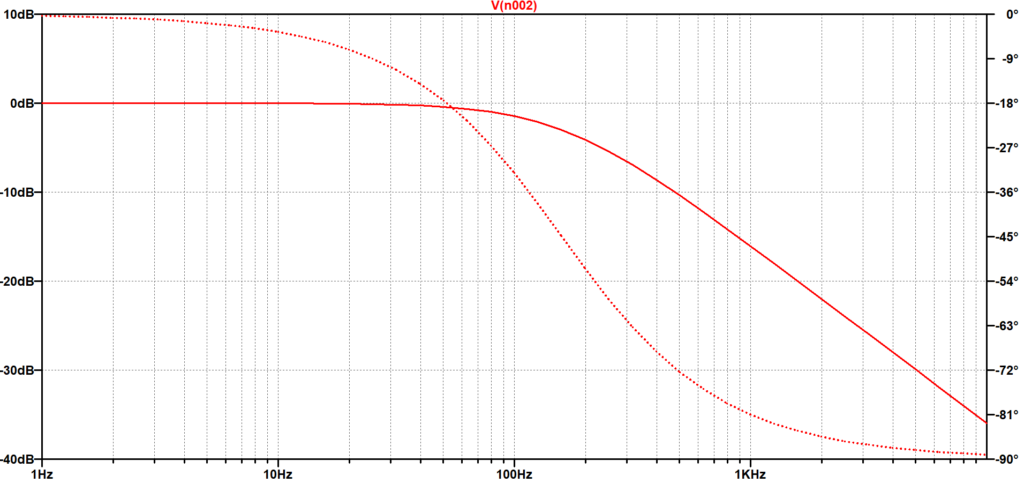
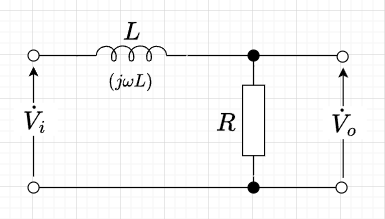
図4は、「R-L 1次LPFの回路図である。\(R,\;L\)に流れる電流を\(\dot{I}\)とすると、図より、次の式が成り立つ。$$\dot{V}_i=\left( R + j \omega L\right) \dot{I} \\ \dot{V}_o = R \dot{I}$$ この2式より、$$\dot{V}_o = \frac{R}{R + j \omega L} \dot{V}_i= \frac{1}{1 + j \frac{\omega L}{R}} \dot{V}_i$$となる。
従って、振幅特性\(|A(j\omega)|\)は$$|A(j \omega)| = \frac{1}{\sqrt{1 +(\frac{\omega L}{R})^2}}$$であり、位相特性\(arg[A(j \omega)]\)は、$$arg[A(j \omega)] = - \tan^{-1} \frac{\omega L}{R}$$である。このとき時定数は、\(\tau = \frac{L}{R}\) [s]である。
振幅特性、位相特性の式から分かるように、周波数特性は図3と同様になる。
ハイパスフィルター(High-Pass Filter:HPF)
図5は、「R-C 1次HPFの回路図」である。\(R,\;C\)に流れる電流を\(\dot{I}\)とすると、図より次の式が成り立つ。$$\dot{V}_i=\left( \frac{1}{j \omega C} + R\right) \dot{I} \\ \dot{V}_o = R \dot{I}$$ この2式より、$$\dot{V}_o = \left(\frac{R}{R + \frac{1}{j \omega C}}\right) \dot{V}_i \\ = \frac{j \omega CR}{1 + j \omega C R} \dot{V}_i$$となる。従って、振幅特性\(|A(j\omega)|\)は$$|A(j \omega)| = \frac{\omega CR}{\sqrt{1 +(\omega C R)^2}}$$であり、位相特性\(arg[A(j \omega)]\)は、$$arg[A(j \omega)] = \frac{\pi}{2} - \tan^{-1} \omega C R$$である。
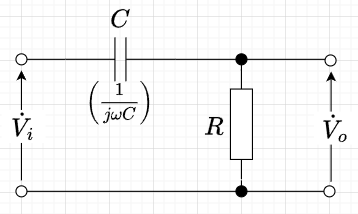
振幅特性の式より、振幅が\(1/\sqrt{2}\)(\(-3dB\))になる角周波数(遮断周波数)は\(\omega_C=\frac{1}{CR}\) [rad/s](周波数\(f_C=\frac{1}{2\pi CR}\) [Hz])である。また、位相は\(45\;\)度となる。なお、\(\tau =CR\) [s]を時定数という。
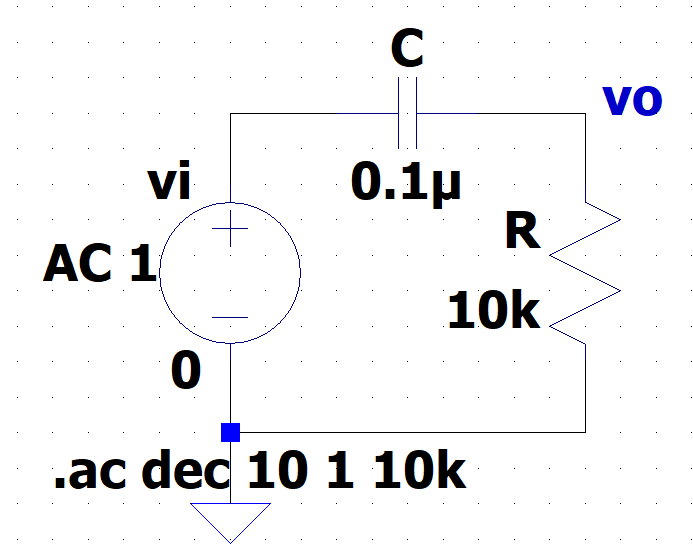
図6「R-C1次HPF(LTspice)」は、AC解析(周波数特性)用のLTspice回路図である。抵抗\(R : \;10\;k\Omega\)、コンデンサ\(C:\;0.1\;\mu F\)と設定している。従って、遮断周波数は、$$f_C = \frac{1}{2\pi CR} \approx 159 \; [Hz]$$である。
図7がLTspiceによる解析結果の「R-C1次HPFの周波数特性」で、赤線の実線が振幅特性、破線が位相特性である。遮断周波数\(f_c:159\;Hz\)において、振幅は\(-3\;dB\)、位相は\(45\;\)度となっている。
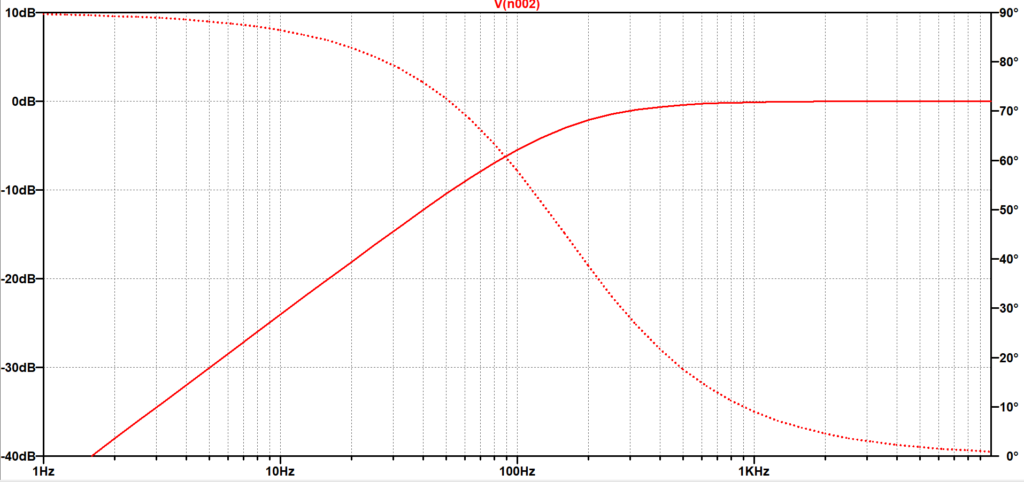
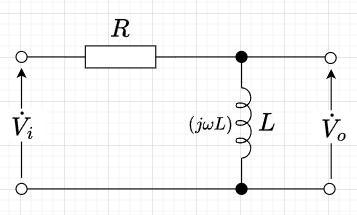
図8は、「R-L 1次HPFの回路図である。\(R,\;L\)に流れる電流を\(\dot{I}\)とすると、図より、次の式が成り立つ。$$\dot{V}_i=\left( R + j \omega L\right) \dot{I} \\ \dot{V}_o = j \omega L \dot{I}$$ この2式より、$$\dot{V}_o = \frac{j \omega L}{R + j \omega L} \dot{V}_i= \frac{j \frac{\omega L}{R} }{1 + j \frac{\omega L}{R}} \dot{V}_i$$となる。
従って、振幅特性\(|A(j\omega)|\)は$$|A(j \omega)| = \frac{\frac{\omega L}{R}}{\sqrt{1 +(\frac{\omega L}{R})^2}}$$であり、位相特性\(arg[A(j \omega)]\)は、$$arg[A(j \omega)] = \frac{\pi}{2}- \tan^{-1} \frac{\omega L}{R}$$である。このとき時定数は、\(\tau = \frac{L}{R}\) [s]である。
振幅特性、位相特性の式から分かるように、周波数特性は図7と同様になる。
バンドパスフィルター(Band-Pass Filter:BPF)
図9は、「BPFの回路図」である。\(C,\;L\)の並列インピーダンスを\(\dot{Z}\)とすると、$$\dot{Z} = \frac{\frac{1}{j \omega C} j\omega L}{\frac{1}{j \omega C} + j \omega L}=\frac{j \omega L}{1 - \omega^2 LC}$$となる。従って、$$\dot{V}_i = \left( R + \dot{Z}\right) \dot{I} \\ \dot{V}_o = \dot{Z} \dot{I}$$が成立し、この2式より、$$\dot{V}_o = \frac{\dot{Z}}{R + \dot{Z}} \dot{V}_i = \frac{j \omega L}{R - \omega^2 LCR + j \omega L} \dot{V}_i$$となる。従って、振幅特性\(|A(j\omega)|\)は$$|A(j \omega)| = \frac{\omega L}{\sqrt{(R - \omega^2 LCR)^2 + (\omega L)^2}}$$であり、位相特性\(arg[A(j \omega)]\)は、$$arg[A(j \omega)] = \frac{\pi}{2} - \tan^{-1} \frac{\omega L}{R - \omega^2 LCR} \;\;\;\;\left(\omega \le \frac{1}{\sqrt{LC}}\right) \\arg[A(j \omega)] = \tan^{-1} \frac{\omega L}{R - \omega^2 LCR} - \frac{\pi}{2} \;\;\;\;\left(\omega \ge \frac{1}{\sqrt{LC}}\right)$$である。
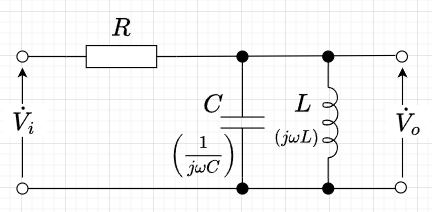
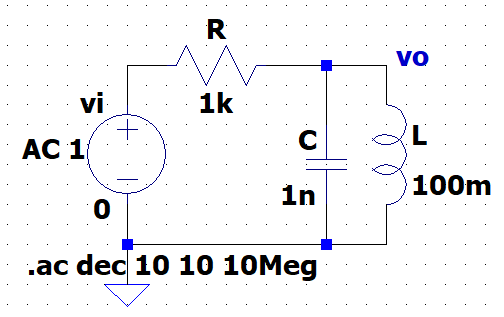
図10「RLC-BPF(LTspice)」は、AC解析(周波数特性)用のLTspice回路図である。抵抗\(R : \;1\;k\Omega\)、コンデンサ\(C:\;1\;nF\)、コイル\(L:\; 100\;mH\)と設定している。
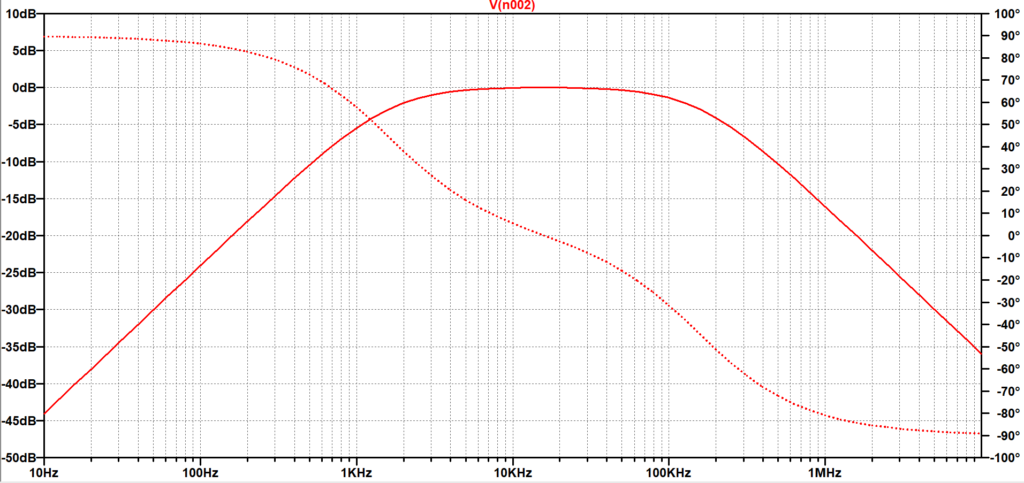
図11がLTspiceによる解析結果の「RLC-BPFの周波数特性」で、赤線の実線が振幅特性、破線が位相特性である。振幅特性は、低域の\(1\;kHz\)以下では\(20\;dB/dec\)で増幅度が増大する。中域(約\(3\;kHz\)から\(90\;kHz\))では一定の増幅度(\(0\;dB\))となり、高域の\(200\;kHz\)以上では、\(-20\;dB/dec\)で増幅度が減少する。
2次LPF
受動素子による2次LPFの構成は各種あるが、ここでは、\(R,\;L,\;C\)による2次LPFを考える。
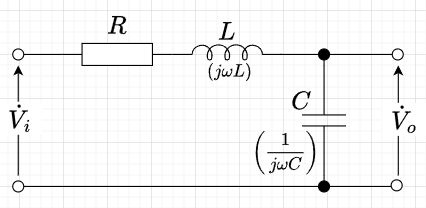
図12は、「RLC-2次LPFの回路図」である。\(R,\;L\,\;C\)に流れる電流を\(\dot{I}\)とすると、図より次の式が成り立つ。$$\dot{V}_i = \left( R + j \omega L + \frac{1}{j \omega C}\right) \dot{I} \\ \dot{V}_o = \frac{1}{j \omega C} \dot{I}$$この2式より、$$\dot{V}_o = \frac{ \frac{1}{j \omega C}}{R + j \omega L+ \frac{1}{j \omega C}} \dot{V}_i \\ = \frac{1}{1 - \omega^2 LC + j \omega RC} \dot{V}_i$$となる。
従って、振幅特性\(|A(j\omega)|\)は$$|A(j \omega)| = \frac{1}{\sqrt{(1 - \omega^2 LC)^2 + (\omega RC)^2}}$$であり、位相特性\(arg[A(j \omega)]\)は、$$arg[A(j \omega)] = - \tan^{-1} \frac{\omega RC}{1 - \omega^2 LC}\;\;\;\;\left(\omega \le \frac{1}{\sqrt{LC}}\right) \\arg[A(j \omega)] = \tan^{-1} \frac{\omega RC}{1 - \omega^2 LC} - \pi\;\;\;\;\left(\omega \ge \frac{1}{\sqrt{LC}}\right) $$である。
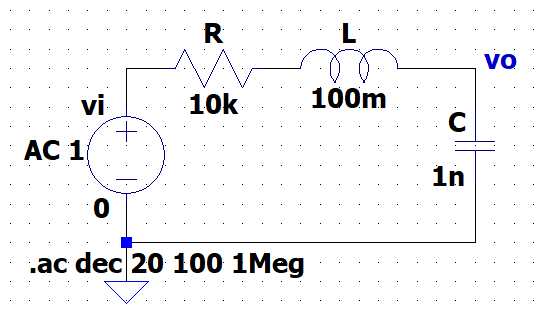
図13「RLC-2次LPF(LTspice)」は、AC解析(周波数特性)用のLTspice回路図である。抵抗\(R : \;10\;k\Omega\)、コイル\(L: \; 100\; mH\)、\コンデンサ\(C:\;1\;nF\)と設定している。
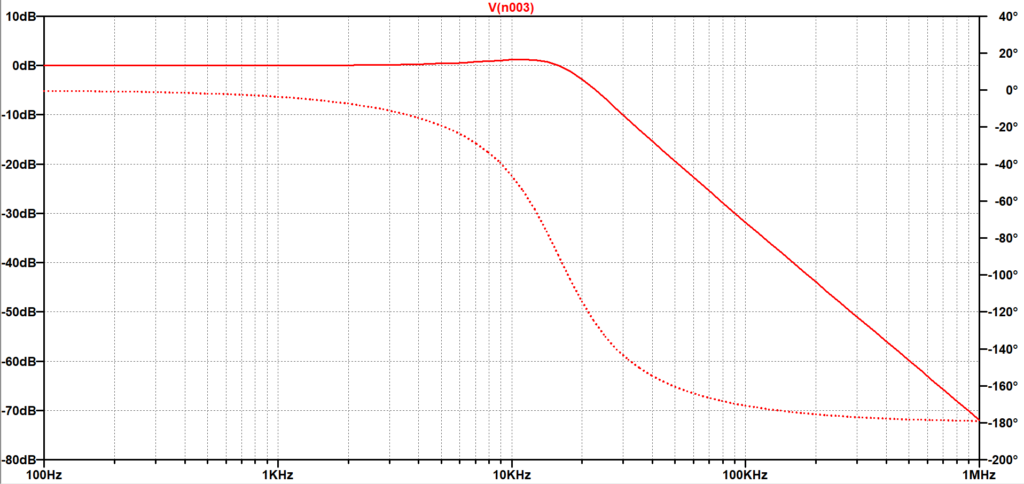
図14がLTspiceによる解析結果の「RLC-2次LPFの周波数特性」で、赤線の実線が振幅特性、破線が位相特性である。振幅特性を見ると\(30 \; kHz\)以上では、\(-40 \; dB/dec\)で増幅度が減少していることが分かる。また、位相特性では、低域では位相\(0\)度で、\(\omega=\frac{1}{\sqrt{LC}}\)において\(-90\)度、高域では位相\(-180\)度となる。


“14. パッシブフィルタ回路” に対して1件のコメントがあります。
コメントは受け付けていません。