24. 極配置法(演習)
式(1)で表記する1入力\(n\)次元定係数線形システムを制御対象とする。$$\dot{x}(t) = A x(t) + b u(t) \\ y(t) = c x(t) \;\;\cdots \cdots (1)$$式(1)のシステムは可観測、可制御とする。さらに、状態変数\(x_1(t) \sim x_n(t)\)が直接観測できるとすると、入力を$$u(t) = -f x(t) \;\;\cdots \cdots(2)$$とすることで、状態フィードバック制御が構成できる。式(2)を式(1)に代入すると、閉ループ系は、$$ \dot{x}(t) = (A - b f)x(t)$$となり、その解は、$$x(t) = \exp[(A - b f)t] \cdot x(0)$$で与えられる。従って、行列\(A - b f\)の全ての固有値を複素平面の左半平面に配置できれば、閉ループ系は漸近安定となる。
固有値の複素平面上での位置と時間応答の関係から、行列\(A - bf\)の全ての固有値を指定し、指定した固有値になるようにフィードバック係数ベクトル\(f\)を求める。手順は、以下である。
1)可制御性の確認(不可制御の場合は、状態フィードバックは不適用)
2)行列\(A - b f\)を求める。
3)\(A - b f\)から閉ループ系の特性方程式を求める。
4)指定したい固有値から閉ループ系特性方程式を求める。
5)3),4)で求めた2つの特性方程式の係数を比較して、フィードバック係数ベクトル\(f\)を求める。
※状態フィードバックの構成図やフィードバック係数の設定などは、14. 状態フィードバック を参照願います。
直接法による極配置
*式(3)のシステムを制御対象として、閉ループ系の固有値を\(-2,\; -3\)とする状態フィードバック係数ベクトル\(f\)を求める。
$$\dot{x}(t) = \begin{bmatrix} 1 & 2 \\ -3 & -4 \end{bmatrix} x(t) + \begin{bmatrix} 2 \\ 3 \end{bmatrix} u(t) \;\; \cdots \cdots (3)$$可制御行列の行列式は、$$|U_c|= \begin{vmatrix} 2 & 8 \\ 3 & -18 \end{vmatrix} = -60 \neq 0$$なので、可制御である。フィードバック係数ベクトル\(f\)を$$f = \begin{bmatrix} f_1 & f_2 \end{bmatrix}$$とする。これより閉ループ系システム行列は、$$A - b f = \begin{bmatrix} 1 & 2 \\ -3 & -4 \end{bmatrix} - \begin{bmatrix} 2 \\3 \end{bmatrix} \begin{bmatrix} f_1 & f_2 \end{bmatrix} \\= \begin{bmatrix} 1 - 2 f_1 & 2 -2 f_2 \\ -3 -3 f_1 & -4 -3 f_2 \end{bmatrix}$$である。従って、閉ループ系の特性方程式は、$$|sI - (A - bf)| = \begin{vmatrix} s - 1 + 2 f_1 & -2 + 2 f_2 \\ 3 + 3 f_1 & s + 4 + 3 f_2 \end{vmatrix} \\= s^2 + (3 + 2 f_1 + 3 f_2) s + (2 + 14 f_1 - 9f_2) = 0 \;\; \cdots \cdots (4)$$指定したい固有値が\(-2,\;-3\)なので、特性方程式は、$$(s + 2)(s + 3) = s^2 + 5s +6 = 0$$この式と式(4)と恒等的に等しくなるためには、\(s\)の各次数の係数どうしが等しくなくてはならない。従って、$$3+2f_1 + 3 f_2 = 5 \\ 2 + 14 f_1 - 9 f_2 = 6$$この連立方程式を解くことで、\(f\)が求まる。$$f = \begin{bmatrix} f_1 & f_2 \end{bmatrix} = \begin{bmatrix} \frac{1}{2} & \frac{1}{3} \end{bmatrix}$$
Scilabによる解法
//状態フィードバック(1)
clear;clf();
//制御対象システムの定義
A=[1 2; -3 -4];
b=[2; 3];
c=[1 0 ; 0 1];
sysP=syslin('c',A,b,c);
//制御対象の固有値
evals=spec(A);
//可制御性のチェック
Uc=cont_mat(A,b);
disp(det(Uc));//行列式の計算
//極配置
poles=[-2 -3];
//状態フィードバック係数の決定
f=ppol(A,b,poles);
cpoles=spec(A-bf); //極配置の確認
//制御対象のインパルス応答
t=0:0.01:10;
y0=csim('impulse',t,sysP);
scf(0);plot(t',y0');
//閉ループ系のインパルス応答
A2=A-bf;
sysP2=syslin('c',A2,b,c);
y=csim('impulse',t,sysP2);
scf(1);plot(t',y');
実行結果
--> evals
evals =
-1. + 0.i
-2. + 0.i
--> Uc
Uc =
2. 8.
3. -18.
--> disp(det(Uc))
-60.
--> f
f = 0.5 0.3333333
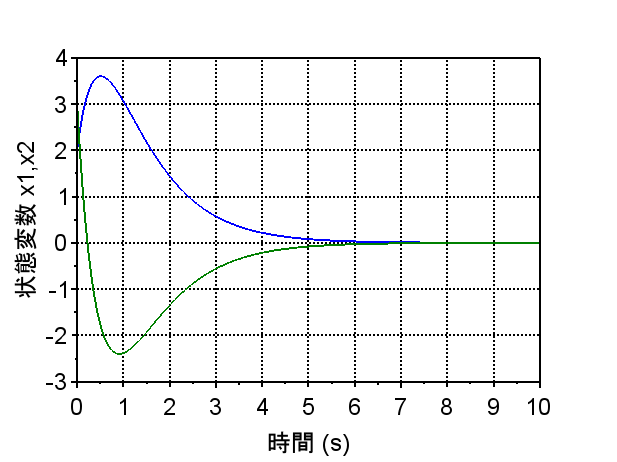
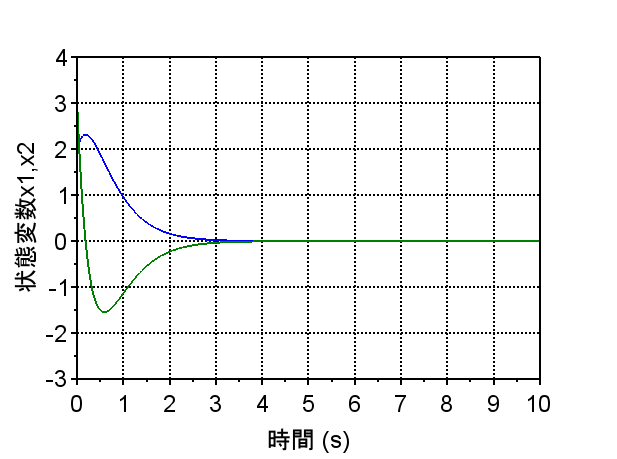
インパルス応答
*式(5)のシステムを制御対象として、閉ループ系の固有値を\(-4\)(3重根)とする状態フィードバック係数ベクトル\(f\)を求める。$$\dot{x}(t) = \begin{bmatrix} -2 & 1 & 0 \\ 1 & -3 & 1 \\ 0 & 1 & -2 \end{bmatrix} x(t) + \begin{bmatrix} 1 \\ 0 \\ 0 \end{bmatrix} u(t) \;\; \cdots\cdots (5)$$
Scilabによる解法
//状態フィードバック(2)
clear;clf();
//制御対象システムの定義
A=[-2 1 0; 1 -3 1 ; 0 1 -2];
b=[1; 0 ; 0];
c=[1 0 0 ; 0 1 0 ; 0 0 1];
sysP=syslin('c',A,b,c);
//制御対象の固有値
evals=spec(A);
//可制御性のチェック
Uc=cont_mat(A,b);
disp(det(Uc));//行列式の計算
//極配置
poles=[-4 -4 -4];
//状態フィードバック係数の決定
f=ppol(A,b,poles);
cpoles=spec(A - b*f); //極配置の確認
//制御対象のインパルス応答
t=0:0.01:5;
y0=csim('impulse',t,sysP);
scf(0);plot(t',y0');
//閉ループ系のインパルス応答
A2=A - b*f;
sysP2=syslin('c',A2,b,c);
y=csim('impulse',t,sysP2);
scf(1);plot(t',y');
実行結果
--> evals
evals =
-4.
-2.
-1.0000000
--> Uc
Uc =
1. -2. 5.
0. 1. -5.
0. 0. 1.
--> disp(det(Uc))
1.
--> f
f = 5. 9. 13.
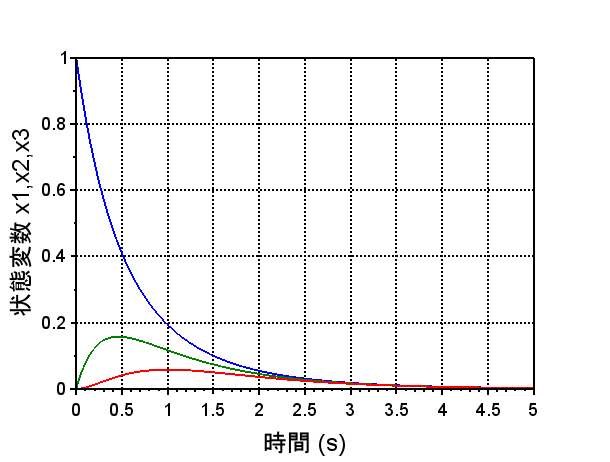
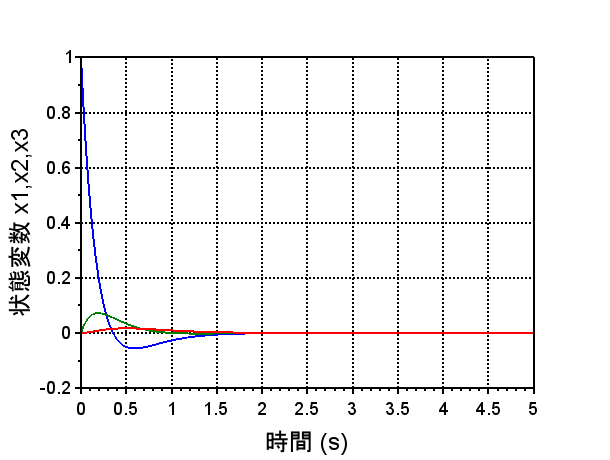
インパルス応答

