20. システムの状態方程式（演習）

システムの特性を以下の状態方程式（式(1)）、出力方程式（式(2)）で表現する。$$\dot{x}(t) = A x(t) + B u(t) \;\;\cdots \cdots (1)\\y(t) = C x(t) \;\;\cdots \cdots (2)$$ \(x(t)\)：状態変数、\(u(t)\)：入力変数、\(y(t)\)：出力変数、\(A\)：システム行列、\(B\)：入力行列、\(C\)：出力行列

※状態方程式の詳細に関しては、3. 動的システムの状態方程式表現 を参照願います。

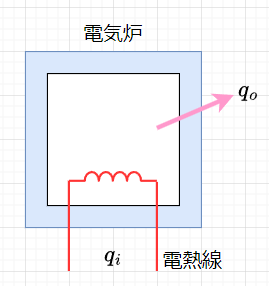
電熱線の単位時間の発生熱量を\(q_i\)、単位時間の熱の放散量を\(q_o\)とするとき、この差が電気炉内の時間的温度変化を与える。微小時間\(\Delta t\)での温度変化を\(\Delta \theta\)とするとき、$$C \Delta \theta = (q_i - q_o) \Delta t$$が成立する。この式の極限を考えると、$$C \frac{d \theta}{dt} = q_i - q_o $$となる。また、放散熱量は、$$q_o = D \theta$$なので、状態方程式は、\(q_i\)を入力変数、\(\theta\)を状態変数として、$$\frac{d \theta}{dt} = -\frac{D}{C} \theta +\frac{1}{C} q_i$$ である。また、炉内の温度を出力として、出力方程式は、$$y = \theta$$となる。

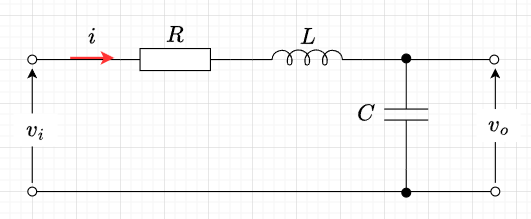
電流\(i\)と入力電圧\(v_i\)の関係は、$$v_i = R i + L \frac{d i}{dt} + \frac{1}{C} \int i dt$$と表せる。これを電荷\(q\)と電圧\(v_i\)の関係式に書き換えると、$$L \frac{d^2 q}{dt^2} + R \frac{d q}{dt} + \frac{1}{C} q = v_i \;\; \cdots\cdots (3)$$となる。なお、\(i = \frac{dq}{dt}, \;\;\; v_o = \frac{1}{C}q\)である。ここで、電荷\(q\)を状態変数\(x_1\)とおく。さらに、$$x_1 = q, \;\;\;\;\;\; \frac{d q}{dt} = \frac{d x_1}{dt } = x_2$$と状態変数\(x_2\)をおくと、式(3)は、$$L \frac{d x_2}{dt} + R x_2 + \frac{1}{C} x_1 = v_i$$であり、$$v_o = \frac{1}{C} x_1$$となる。以上の式をまとめると、$$\frac{d}{dt} \begin{bmatrix} x_1 \\ x_2 \end{bmatrix} = \begin{bmatrix} 0 & 1 \\ - \frac{1}{LC} & -\frac{R}{L} \end{bmatrix} \begin{bmatrix} x_1 \\ x_2 \end{bmatrix} + \begin{bmatrix} 0 \\ \frac{1}{L} \end{bmatrix} u \\ y = \begin{bmatrix} \frac{1}{C} & 0 \end{bmatrix} \begin{bmatrix} x_1 \\ x_2 \end{bmatrix} $$となる。ここで、\(u\)：入力変数、\(y\)：出力変数である。

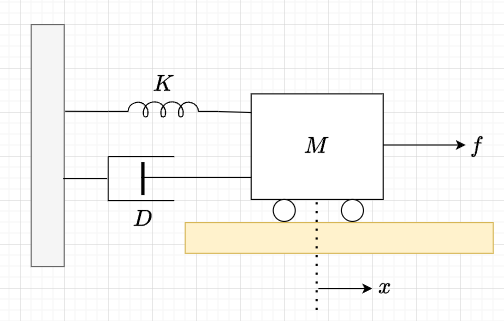
台車と床の間の摩擦をゼロとすると、力の釣り合いの式は、$$M\frac{d^2 x}{dt^2} + D \frac{d x}{dt} + K x = f\;\;\cdots \cdots(4)$$となる。ここで、状態変数を\(x_1 = x , \;\;\;\;\; x_2 = \frac{x_1}{dt}\)とおくと、式(4)は、$$M\frac{d x_2}{dt} + D x_2 + K x_1 = f$$となる。外力\(f\)を入力変数\(u\)、位置\(x\)を出力変数\(y\)として、まとめると、$$\frac{d}{dt}\begin{bmatrix} x_1 \\ x_2 \end{bmatrix} = \begin{bmatrix} 0 & 1 \\ - \frac{K}{M} & - \frac{D}{M} \end{bmatrix} \begin{bmatrix} x_1 \\ x_2 \end{bmatrix} + \begin{bmatrix} 0 \\ \frac{1}{M} \end{bmatrix} u \\ y = \begin{bmatrix} 1 & 0 \end{bmatrix} \begin{bmatrix} x_1 \\ x_2 \end{bmatrix} $$となる。

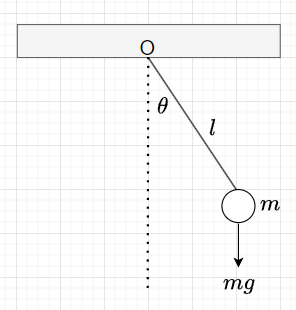
よって、運動方程式は、$$m l^2 \frac{d^2 \theta}{dt^2} = - l m g \sin \theta \\ \frac{d^2 \theta}{dt^2} = - \frac{g}{l} \sin \theta\;\;\cdots \cdots (5)$$となる。この式は、三角関数が含まれているため非線形微分方程式である。しかし、振れ角\(\theta\)が小さい場合には、\(\sin \theta = \theta\)とできるので、式(5)は、$$\frac{d^2 \theta}{dt^2} = - \frac{g}{l} \theta$$となる。ここで、\(x_1 = \theta , \;\; x_2 = \frac{d x_1}{dt}\)とおくと、$$\frac{d x_2}{dt} = -\frac{g}{l} x_1$$なので、振り子運動の状態方程式は、$$\frac{d}{dt} \begin{bmatrix} x_1 \\ x_2 \end{bmatrix} = \begin{bmatrix} 0 & 1 \\ -\frac{g}{l} & 0 \end{bmatrix} \begin{bmatrix} x_1 \\ x_2 \end{bmatrix}$$となる。但し、\(\theta\)は小さく、\(\sin \theta = \theta\)と見なせる範囲とする。

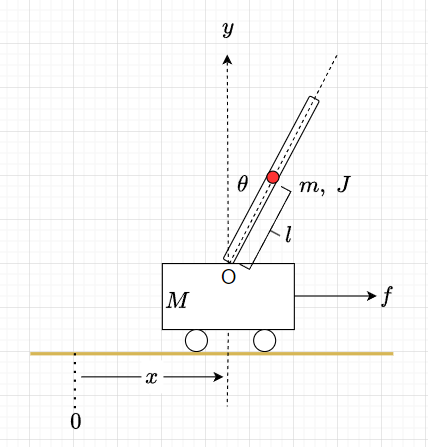
よって、振子の並進運動のエネルギーは、$$\frac{1}{2} m v^2 = \frac{1}{2} m(\dot{x}^2_G + \dot{y}^2_G) = \frac{1}{2} m \left( \dot{x}^2 + 2 \dot{x} l \dot{\theta} \cos \theta + l^2 \dot{\theta}^2 \right)$$ である。これに、振子の回転運動と台車の運動エネルギーを加えた運動エネルギーの総和\(T\)は、$$T = \frac{1}{2} J \dot{\theta}^2 + \frac{1}{2} M \dot{x}^2 + \frac{1}{2} m \left( \dot{x}^2 + 2 \dot{x} l \dot{\theta} \cos \theta + l^2 \dot{\theta}^2 \right)$$となる。また、ポテンシャルエネルギーは、$$U = m g l \cos \theta$$である。従って、ラグラジアン\(L\)は、$$L = T - U = \frac{1}{2}(M + m)\dot{x}^2 + m \dot{x} l \dot{\theta} \cos \theta + \frac{1}{2}(J + m l^2)\dot{\theta}^2 - m g l \cos \theta$$となる。ラグランジュの運動方程式、$$\frac{d}{dt}\left(\frac{\partial L}{\partial \dot{q}}\right) - \frac{\partial L}{\partial q} = 0$$より、\(\theta\)を一般化座標として、$$\frac{\partial L}{\partial \theta} = - m l \dot{x} \dot{\theta} \sin \theta + m g l \sin \theta \\ \frac{d}{dt} \left(\frac{\partial L}{\partial \dot{\theta}}\right) = \frac{d}{dt} \left\{ m l \dot{x} \cos \theta + ( J + m l^2) \dot{\theta} \right\} = m l \ddot{x} \cos \theta - m l \dot{x} \dot{\theta} \sin \theta + (J + m l^2)\ddot{\theta}$$を得る。よって、ラグランジュの運動方程式は、$$m l \ddot{x} \cos \theta + (J + m l^2)\ddot{\theta} - m g l \sin \theta =0 \;\; \cdots \cdots (6)$$である。同様に、\(x\)を一般化座標とすると、$$\frac{\partial L}{\partial x} = 0 \\ \frac{d}{dt} \left(\frac{\partial L}{\partial \dot{x}}\right) = \frac{d}{dt} \left\{ (M + m)\dot{x} + m l \dot{\theta} \cos \theta \right\} = (M + m)\ddot{x} + m l \ddot{\theta} \cos \theta - m l \dot{\theta}^2 \sin \theta$$を得る。この場合は、外力\(f\)があるので、ラグランジュの運動方程式は、$$(M + m)\ddot{x} + m l \ddot{\theta} \cos \theta - m l \dot{\theta}^2 \sin \theta = f \;\; \cdots \cdots (7)$$である。式(6)、式(7)において、傾き角\(\theta\)が小さいとして線形化すると、$$m l \ddot{x} + (J + m l^2)\ddot{\theta} - m g l \theta = 0 \\ (M + m) \ddot{x} + m l \ddot{\theta} = f$$となる。この連立微分方程式を\(\ddot{x} ,\; \ddot{\theta}\)について解いて、状態方程式の形式にまとめると、$$ \frac{d}{dt} \begin{bmatrix} x \\ \theta \\ \dot{x} \\ \dot{\theta} \end{bmatrix} = \begin{bmatrix} 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ 0 & -\frac{m^2 l^2 g}{A} & 0 & 0 \\ 0 & \frac{(M + m) m g l}{A} & 0 & 0 \end{bmatrix} \begin{bmatrix} x \\ \theta \\ \dot{x} \\ \dot{\theta} \end{bmatrix} + \begin{bmatrix} 0 \\ 0 \\ \frac{J + m l^2}{A} \\ - \frac{m l}{A} \end{bmatrix} f $$ここで、\(A = (M + m)(J + m l^2) - m^2 l^2\)である。

※倒立振子実験装置については、https://www.pid-control.com/products/seesaw/index.htmlを参照願います。