3. 動的システムの状態方程式表現
ある時点での出力がその時点の入力だけに依存するシステムを静的システムと呼び、出力がその時点と、過去の入力や現象が始まったときの内部状態に依存するシステムを動的システムと呼ぶ。動的システムでは、過去の入力を記憶したり、内部状態を示す状態変数が必要となる。
動的システムは、一般的に微分方程式を使って記述する。特に常微分方程式で表される動的システムを集中定数システムといい、以下、集中定数システムについて考える。
状態変数が\(n\)個の\(x_1(t),x_2(t),\cdots, x_n(t)\)、
入力変数が\(m\)個の\(u_1(t),u_2(t), \cdots, u_m(t)\)、
出力変数が\(l\)個の\(y_1(t),y_2(t),\cdots,y_l(t)\) のシステムを考える。これらをベクトルで表し、
\(\boldsymbol{x}(t) = \begin{bmatrix} x_1(t) \\ x_2(t) \\ \vdots \\ x_n(t) \end{bmatrix}\) , \(\boldsymbol{u}(t) = \begin{bmatrix} u_1(t) \\ u_2(t) \\ \vdots \\ u_m(t) \end{bmatrix}\) , \(\boldsymbol{y}(t) = \begin{bmatrix} y_1(t) \\ y_2(t) \\ \vdots \\ y_l(t) \end{bmatrix}\) とする。
\(\boldsymbol{x}(t)\)を状態変数ベクトル、\(\boldsymbol{u}(t)\)を入力変数ベクトル、\(\boldsymbol{y}(t)\)を出力変数ベクトルという。
動的システムは、単一の\(n\)階、または、複数の高階の常微分方程式で記述されるが、現代制御理論では、連立\(n\)次の1階常微分方程式によって表す。$$\frac{d\boldsymbol{x}(t)}{dt}=\boldsymbol{f}(\boldsymbol{x}(t),\boldsymbol{u}(t))$$を状態方程式、$$\boldsymbol{y}(t)=\boldsymbol{g}(\boldsymbol{x}(t),\boldsymbol{u}(t))$$を出力方程式という。線形時不変システムでは、
状態方程式:$$\boldsymbol{\dot{x}} (t) = \boldsymbol{A} \boldsymbol{x}(t) + \boldsymbol{B} \boldsymbol{u}(t)$$ 出力方程式:$$\boldsymbol{y}(t) = \boldsymbol{C}\boldsymbol{x}(t) + \boldsymbol{D}\boldsymbol{u}(t)$$ と表す。
\(\boldsymbol{A}\)をシステム行列(または、状態行列)、\(\boldsymbol{B}\)を入力行列(または、駆動行列)、\(\boldsymbol{C}\)を出力行列、\(\boldsymbol{D}\)を直達行列という。
※線形時不変システム(linear time-invariant system, LTIシステム)は、入力信号に対して線形かつ時不変性なシステムである。つまりシステムの応答が入力信号の重ね合わせに対して線形で、時間によらず一定の応答を示すという性質を持つシステムのことである。
※直達行列\(\boldsymbol{D}\)は零行列とすることが多い。これは、通常、制御入力と出力との間に直接的な関係がなく、入力が状態変数を通して出力に影響するためで、直達行列を零行列で考えても多くの場合問題ない。ただし、制御システムの設計や解析においては、直達行列が非ゼロである場合も考慮する必要がある。
状態方程式の例(電気系)
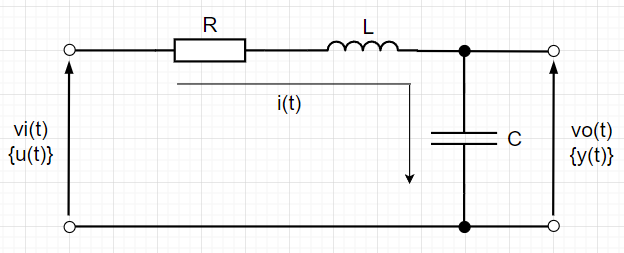
回路方程式は、$$R i(t)+L\frac{di(t)}{dt} + v_o(t) = v_i(t) \;\;\; \cdots \cdots(1)$$ $$i(t) = C\frac{dv_o(t)}{dt} \;\;\; \cdots \cdots(2)$$ $$\frac{di(t)}{dt}=C\frac{d^2v_o(t)}{dt^2} \;\;\; \cdots \cdots(3)$$ $$LC\frac{d^2v_o(t)}{dt^2} +RC\frac{dv_o(t)}{dt} +v_o(t) = v_i(t) \;\;\; \cdots \cdots(4)$$となる。入力電圧\(v_i(t) = u(t)\)、出力電圧\(v_o(t) = y(t)\)、また、キャパシタ\(C\)の両端の電圧を状態変数\(x_1(t)\)、抵抗\(R\)に流れる電流\(i(t)\)を状態変数\(x_2(t)\)とおく。\((2)\)式より、\(x_2(t) = C\dot{x_1}(t)\)なので、\(\dot{x_1}(t) = \frac{1}{C} x_2(t)\)、また\((1)\)式より、\(R x_2(t) + L \dot{x_2}(t) + x_1(t) = u(t)\)なので、\(\dot{x_2}(t) = -\frac{1}{L}x_1(t) - \frac{R}{L}x_2(t) + \frac{1}{L} u(t)\)となる。また、\(y(t) = v_o(t) = x_1(t)\)である。
以上をまとめると、
状態方程式:$$\begin{bmatrix} \dot{x_1}(t) \\ \dot{x_2}(t) \end{bmatrix} = \begin{bmatrix} 0 & \frac{1}{C} \\ -\frac{1}{L} & -\frac{R}{L} \end{bmatrix} \begin{bmatrix} x_1(t) \\ x_2(t) \end{bmatrix} + \begin{bmatrix} 0 \\ \frac{1}{L} \end{bmatrix} u(t)$$ 出力方程式:$$y(t) = \begin{bmatrix} 1 & 0 \end{bmatrix} \begin{bmatrix} x_1(t) \\ x_2(t) \end{bmatrix}$$となる。
状態方程式の例(機械系)
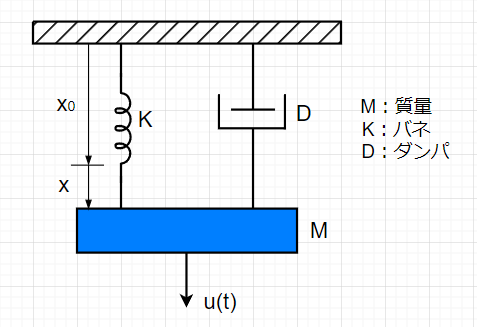
\(u(t)\)を入力としての外力として、重力とのつりあいの位置を\(x_0\)として、そこからの質量の変位を\(x(t)\)とする。質量に対して上向きに\(Kx(t)\)、\(Dv(t)=D\dot{x}(t)\)、\(Ma = M\ddot{x}(t)\)の力が加わり、下向きに\(u(t)\)が加わっているので、力のつり合いの式は、$$M\ddot{x}(t) + D\dot{x}(t) + Kx(t) = u(t) \;\;\; \cdots (5)$$ となる。状態変数として、\(x(t) = x_1(t)\)、\(\dot{x}(t) = x_2(t)\)とすると\(\dot{x_1}(t) =x_2(t)\)。(5)式より、$$M\dot{x_2}(t) + D x_2(t) + K x_1(t) = u(t)$$となる。これを行列で表すと、
状態方程式:$$\begin{bmatrix} \dot{x_1}(t) \\ \dot{x_2}(t) \end{bmatrix} = \begin{bmatrix} 0 & 1 \\ -\frac{K}{M} & -\frac{D}{M} \end{bmatrix} \begin{bmatrix} x_1(t) \\ x_2(t) \end{bmatrix} + \begin{bmatrix} 0 \\ \frac{1}{M} \end{bmatrix} u(t)$$ 出力方程式(質量の変位\(x(t)\)を出力とする):$$y(t) = \begin{bmatrix} 1 & 0 \end{bmatrix} \begin{bmatrix} x_1(t) \\ x_2(t) \end{bmatrix}$$となる。
状態方程式の例(電気ー機械系)
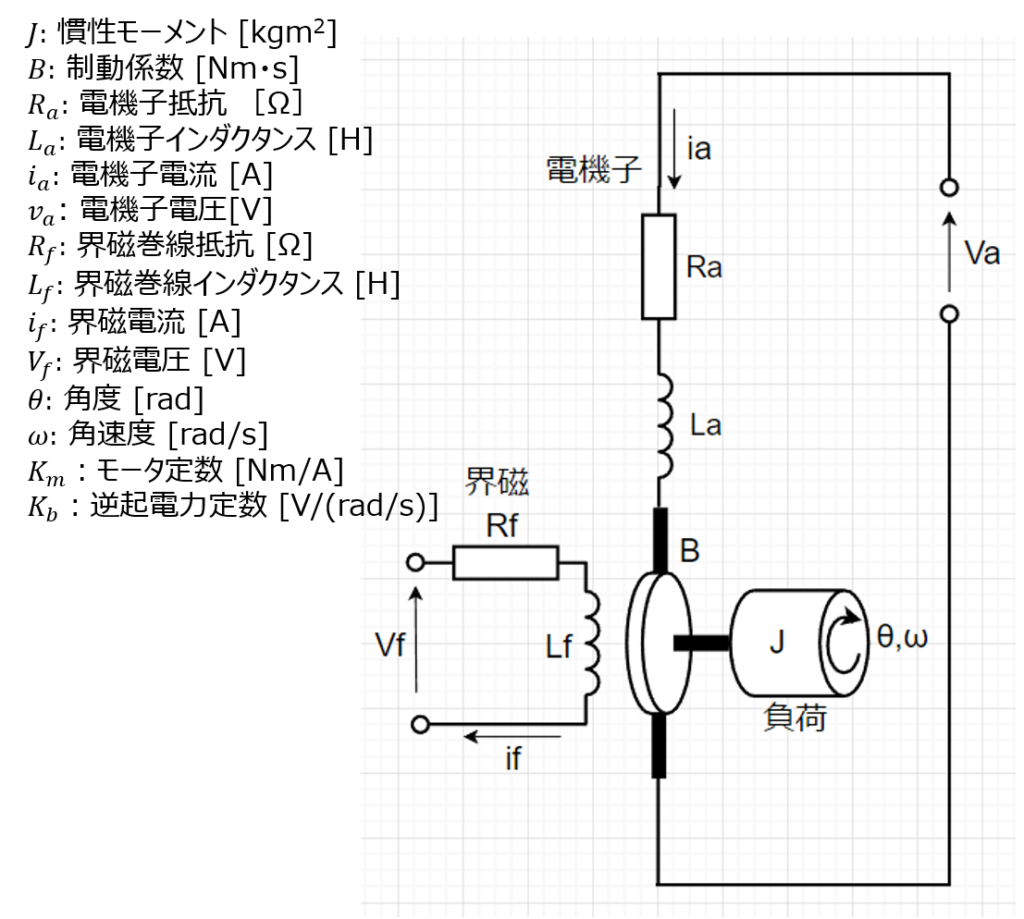
図はDCサーボモータの模式図である。制動係数(粘性摩擦係数)\(B\)と慣性モーメント\(J\)の負荷に接続され、回転角\(\theta(t)\)で回転するサーボモータである。
電機子電流制御方式(定励磁制御)のモデルで考える。この場合、界磁電流\(I_f\)一定とする。(界磁に永久磁石を使用する小型DCモータの場合と同等である。)
また、入力を電機子電圧\(v_a(t)\)とする。電機子回路の起電力のつり合いから、$$v_a(t) = L_a \dot{i_a}(t) + R_a i_a(t)+ v_b(t)$$ $$ v_b(t) = K_b \omega(t) = K_b \dot{\theta}(t)$$となる。ここで、\(v_b(t)\)はモータの回転による逆起電力である。発生トルクと消費トルクのつり合いから、$$K_m i_a(t) = J \ddot{\theta}(t) + D \dot{\theta}(t)$$ ここで、状態変数を\(x_1(t) = \theta (t)\)(回転角)、\(x_2(t) = \dot{\theta}(t)\)(角速度)、\(x_3(t) = i_a(t)\)(電機子電流)とし、入力を\(u(t) = v_a(t)\)とする。また、\(\dot{x_1}(t) = x_2(t)\)である。$$\boldsymbol{x(t)} = \begin{bmatrix} x_1(t) \\ x_2(t) \\ x_3(t) \end{bmatrix} = \begin{bmatrix} \theta(t) \\ \dot{\theta}(t) \\ i_a(t) \end{bmatrix}$$
以上から、
状態方程式:$$\boldsymbol{\dot{x}(t)} =\begin{bmatrix} 0 & 1 & 0 \\ 0 & -\frac{D}{J} & \frac{K}{J} \\ 0 & -\frac{K}{L_a} & -\frac{R_a}{L_a} \end{bmatrix} \boldsymbol{x(t)} + \begin{bmatrix} 0 \\ 0 \\ \frac{1}{L_a} \end{bmatrix} u(t)$$ 出力方程式(回転角を出力とする):$$y(t) = \begin{bmatrix} 1 & 0 & 0 \end{bmatrix} \boldsymbol{x(t)}$$


“3. 動的システムの状態方程式表現” に対して2件のコメントがあります。
コメントは受け付けていません。