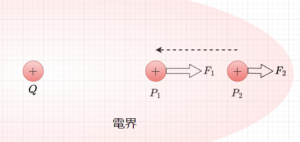
3. 電気力線と電束、ガウスの定理

電気力線

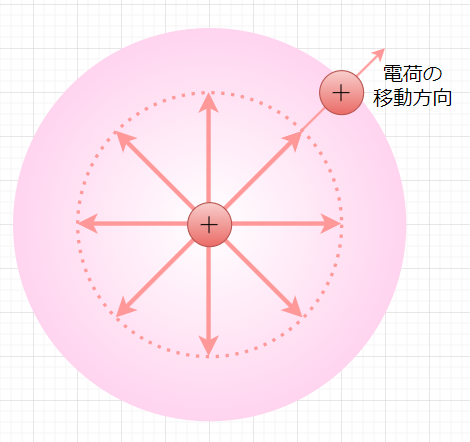
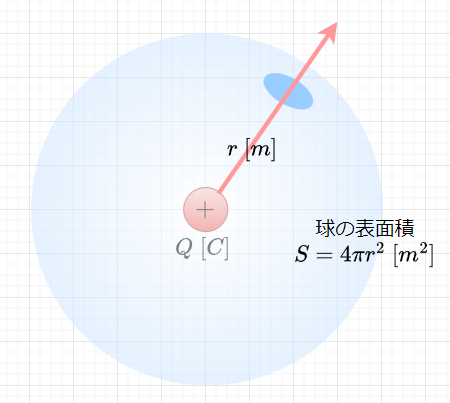
図１に示すように、空間中に置かれた点電荷のつくる電界中に微小な点電荷を置いたとすると、この微小な点電荷は静電力により、1本の軌跡を描いて移動すると想像される。この軌跡の線を電気力線と考える。図１の中心にある電荷から四方八方（球状）に電気力線が出ていると考えることができる。このように電気力線は、電界の状態（方向、大きさ、分布）を表現するための仮想の線といえる。図２に示すように、電気力線は次のように定めて取り扱う。
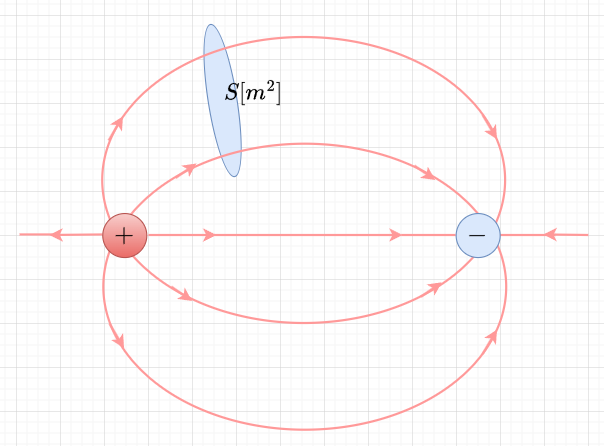
（１）電気力線は、正電荷から出て負電荷に入る。電気力線が途中で消えることはない。
（２）電気力線の方向（接線方向）がその点の電界の方向を表す。
（３）電気力線の密度でその面上の電界の強さを表す。
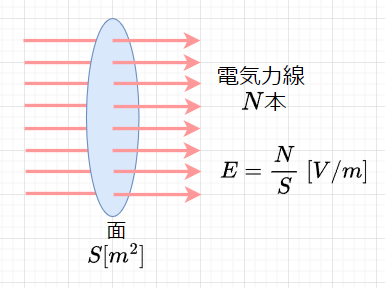
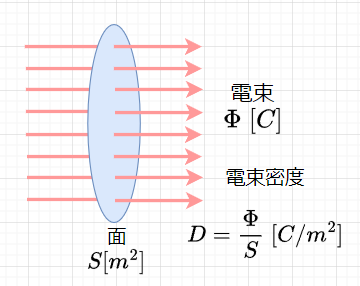
図３より、電界の強さを、面積\(S \;[m^2]\)の面を垂直に通る電気力線数\(N\)として、$$E = \frac{N}{S} \;[本/m^2]$$（電気力線密度）と表す。
さらに、図４に示すように球体をイメージして、点電荷から放射状に電気力線が出ると考えれば、単位面積当たりの電気力線密度は、電荷からの距離の２乗に反比例（球面積に反比例）する。$$E = \frac{N}{S} = \frac{N}{4 \pi r^2} \;[本/m^2]$$また、真空中で考えると、電界の強さはクーロンの法則から、$$E=\frac{F}{Q} = \frac{Q}{4 \pi \epsilon_0 r^2} \;[V/m]$$なので、電気力線数\(N\)は、$$N = SE =4 \pi r^2 \frac{Q}{4 \pi \epsilon_0 r^2} = \frac{Q}{\epsilon_0}$$である。電気力線は、真空中では\(+Q\;[C]\)から\(Q/\epsilon_0\)[本］出て、\(-Q\;[C]\)へ\(Q/\epsilon_0\)[本］入ると考えられる。また、一般の媒質内（誘電体内）では、$$N = \frac{Q}{\epsilon} = \frac{Q}{\epsilon_0 \epsilon_s} \; [本］$$となる。なお、電気力線は仮想的なものなので、単位の［本］自体には意味はない。

電束、電束密度

電束は誘電率に無関係に電荷の量のみで定まる「束」を定義したもので、これにより、電荷\(Q\)、誘電率\(\epsilon\)、誘電体内の電界の強さ\(E\)を明確に表現できる。

ガウスの定理

ガウスの定理とは、「ある任意の閉曲面から外に出る電気力線数は、その閉曲面内にある電荷の総和の\(1/ \epsilon_0\)に等しい」である。
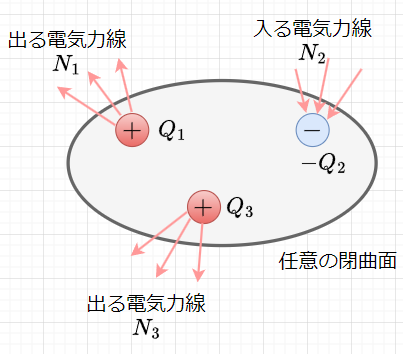
例えば、図６のように閉曲面の内に電荷\(Q_1, \; -Q_2, \;Q_3\)があるとすると、閉曲面から出る電気力線の総数は、$$N = N_1 + (-N_2) + N_3 \\= \frac{1}{\epsilon_0} \left\{Q_1 + (-Q_2) + Q_3 \right\}$$となる。一般的には、$$N = \frac{\sum Q}{\epsilon_0}$$と書ける。すなわち、閉曲面内にある電荷と閉曲面の面積が球面面積の計算可能な面であれば、閉曲面上の電界の強さを知ることができることを意味する。ただし、面積\(S\)から出る電気力線が面上のどの点でも直角で一様である場合に成立する。
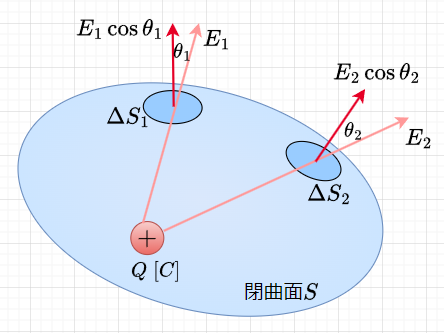
次に、球面以外の閉曲面内に電荷\(Q \;[C]\)がある場合、面上の電界の強さが一様でない場合や電気力線が面に垂直でない場合を考える必要がある。この場合、図７のように任意の形状の閉曲面\(S\)に微小面積\(\Delta S\)をとる。この\(\Delta S\)上の電界は一様と見なせるので、\(\Delta S\)での電界の強さを\(E\)として、法線方向の成分を\(E_n\)とすると、\(E_n\)は\(\Delta S\)面に対して垂直な電気力線密度を表しており、$$E_n = E \cos \theta$$となる。但し、\(\theta\)は\(E\)と\(E_n\)とのなす角である。よって、\(\Delta S\)から外に出る電気力線数\(\Delta N\)は、$$\Delta N = E \cos \theta \cdot \Delta S$$である。これを閉曲面\(S\)全てにわたって微小部分\(\Delta S\)に分割して、それぞれの電気力線を\(\Delta N_1 ,\; \Delta N_2 ,\;\cdots \)として、その総和を求める。$$N = E_1 \cos \theta_1 \Delta S_1 + E_2 \cos \theta_2 \Delta S_2 + \cdots$$であり、$$N = \sum E \cos \theta \cdot \Delta S = \sum E_n \cdot \Delta S$$ また、閉曲面内から出る電気力線数は、\(N = Q/ \epsilon_0\)なので、ガウスの定理は、$$\frac{Q}{\epsilon_0} = \sum E_n \cdot \Delta S$$となる。このガウスの定理を積分形式で書くと、$$\oint_S \boldsymbol{E}\cdot d\boldsymbol{S} = \frac{Q}{\epsilon_0} = \frac{1}{\epsilon_0} \int_V \rho d \boldsymbol{V}$$となる。なお、\(\rho \;[C/m^3]\)は電荷密度 である。
ガウスの定理は、電荷が分布する大きさのある帯電体による物体周辺の電界の強さや、物体の内部に分布する電荷と物体内部の電界の強さとの関係などを知る場合に活用される。

※法線：曲面上の一点で、その点での接平面に垂直な直線。