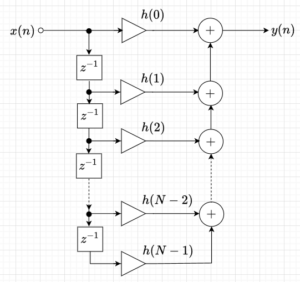
13. FIRフィルタの設計
FIRフィルタの設計では、フーリエ級数展開法で求めたインパルス応答に窓関数を掛ける窓関数法が代表的である。
窓関数法によるフィルタの設計手順は、以下である。
1)仕様決定:
・フィルタの種類(LPF、HPF、BPF、BRFなど)
・カットオフ周波数、阻止域減衰量、許容されるリップル量の決定
2)窓関数の選択
・矩形窓、ハミング窓、カイザー窓など、様々な窓関数があり、各窓関数によって、周波数特性やリップル量が異なる。必要な仕様を満たせる窓関数を、特性比較表などを参考に選択する。
3)フィルタ長の決定
・窓関数のメインローブの幅と必要な阻止域減衰量からフィルタ長を決定する。(フィルタ長が長いほど阻止域減衰量は大きくなるが、計算量が増える。)
4)フィルタ係数の計算
・理想的なフィルタの周波数特性をフーリエ変換して、時間領域でのインパルス応答を求める。
・選択した窓関数でインパルス応答を窓化し、FIRフィルタの係数を求める。
5)特性評価
・設計したフィルタの周波数特性を計算し、仕様を満たしているか確認する。
・必要に応じて窓関数やフィルタ長を変更して、再度設計を行う。
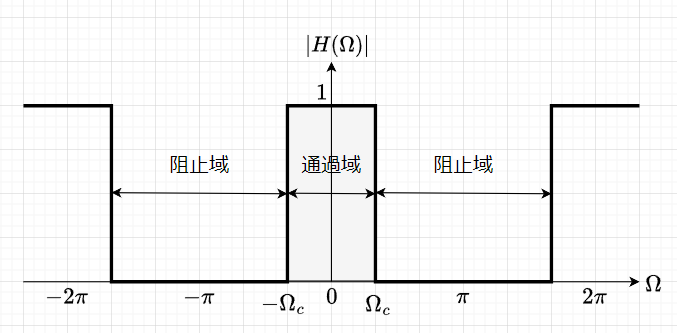
理想低域フィルタのインパルス応答
図1に理想LPFの周波数特性例を示す。このような理想LPFの伝達関数は、$$H(\Omega) = \left\{ \begin{array}{ll} 1 & (|\Omega| < \Omega_c) \\ 0 & (\Omega_c < |\Omega| < \pi) \end{array} \right.$$ である。このインパルス応答\(h(n)\)は、$$h(n) = \frac{1}{2\pi} \int_{-\pi}^{\pi} H_d(\Omega)e^{j \Omega n} d \Omega \\ = \frac{1}{2\pi} \int_{-\Omega_c}^{\Omega_c} e^{j \Omega n} d \Omega \\ = \frac{1}{2\pi} \frac{1}{j n} \left[e^{j \Omega n} \right]_{-\Omega_c}^{\Omega_c} \\ = \frac{1}{2\pi} \frac{1}{j n} \left(e^{j \Omega_c n} - e^{-j \Omega_c n}\right) \\ = \frac{\sin \Omega_c n}{n \pi}$$となる。ここで、\(\Omega_c = \frac{\pi}{4}\)のときは、$$h(n) = \frac{\sin(n\pi/4)}{n \pi} \\ = \frac{1}{4} \frac{\sin(n \pi /4)}{n \pi /4} \\ = \frac{1}{4} \rm{sinc}(n \pi /4) $$である。ここで、\(\rm{sinc}\)関数を$$\rm{sinc}(x) = \frac{\sin(x)}{x}$$と定義する。
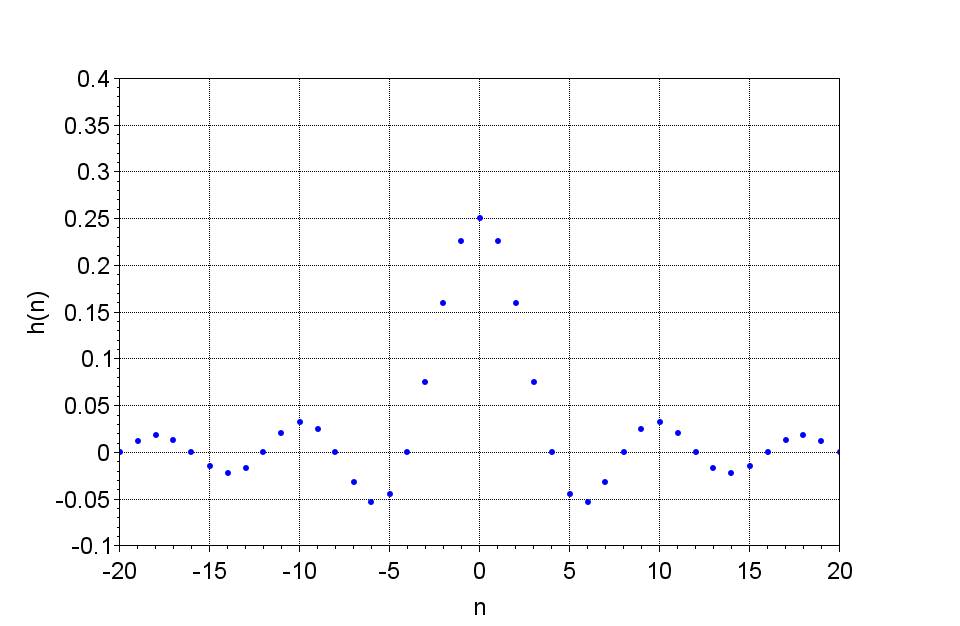
図2が理想LPFのインパルス応答である。この図のように理想LPFのインパルス応答は、\(-\infty<n<\infty\)の無限区間に広がることになる。
Scilabスクリプト
//理想LPFのインパルス応答
clear; clf();
pi=%pi;
n=-20:1:20;
h=(1/4)sinc(n*pi/4); //sinc関数を使用
plot(n,h,'.')
FIRフィルタ設計の基本
理想低域フィルタのインパルス応答は、$$h(n) = \frac{\Omega_c}{\pi} \rm{sinc}(n \Omega_c)$$で与えられる。このインパルス応答の係数から低域FIRフィルタを基本的には実現できるが、問題点が2点ある。つまり、
1)インパルス応答が無限区間に存在しているので、実装不可能。
2)インパルス応答が負の領域にも存在するので、因果性に反する。
の2点である。1)は、無限系列\(h(n)\)のインパルス応答を適当な区間で打ち切り有限数列とする。また、2)は、一定の遅延時間を与えた係数を用いる。以上により、\(\Omega_c = \frac{\pi}{4}\)としたときのインパルス応答列を図3-1~3のようにインパルス応答列を\(N=\pm 10\)で打ち切り、10ずらすことで、実装が可能となる。
表1にフィルタの係数を示す。係数は、\(n=10\)を中心に対称である。このようにして得られた基本的な低域FIRフィルタの周波数特性を図4に示す。
| n=0 | n=1 | n=2 | n=3 |
| 0.0318310 | 0.0250088 | 0.00 | -0.0321542 |
| n=4 | n=5 | n=6 | n=7 |
| -0.0530516 | -0.0450158 | 0.00 | 0.0750264 |
| n=8 | n=9 | n=10 | n=11 |
| 0.1591549 | 0.2250791 | 0.25 | 0.2250791 |
| n=12 | n=13 | n=14 | \(\cdots\) |
| 0.1591549 | 0.0750264 | 0.00 | \(\cdots\) |
Scilabスクリプト
//周波数特性
clear; clf();
pi=%pi;z=%z;
M=200; N=10;
//理想LPFのインパルス応答
n=-M:1:M;
h=(1/4)*sinc(npi/4);
scf(0);plot(n,h,'.');
//インパルス応答の打ち切り
n=-N:1:N;
h=(1/4)*sinc(npi/4);
scf(1);plot(n,h,'.');
//インパルス応答のシフト(FIRフィルタの係数計算)
n=n+N;
scf(2);plot(n,h,'.');
T=1;
//FIRフィルタの伝達関数
Hz = h(1);
for n=1:2*N,
Hz = Hz + h(n+1).*z^-n;
end;
//システム関数に変換
Hzz=syslin(T,Hz);
//ボード線図の描画
scf(3);bode(Hzz,0.01,4,'rad');
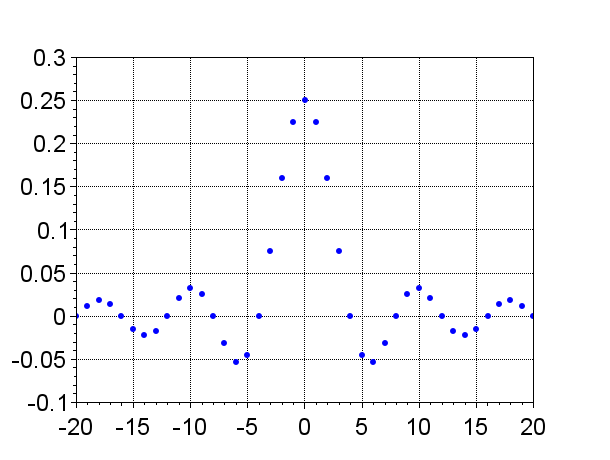
元のインパルス応答列
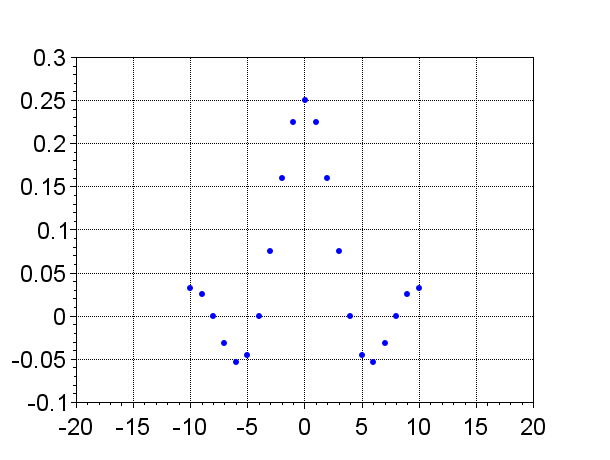
打ち切ったインパルス応答列
\(N=\pm10\)の場合
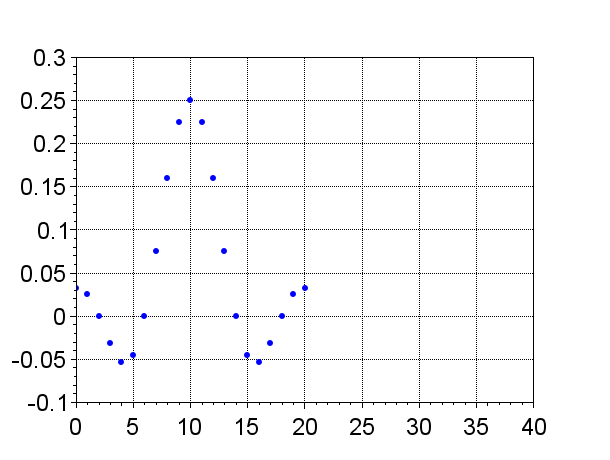
打ち切って、ずらしたインパルス応答列
\(N=\pm10\)の場合
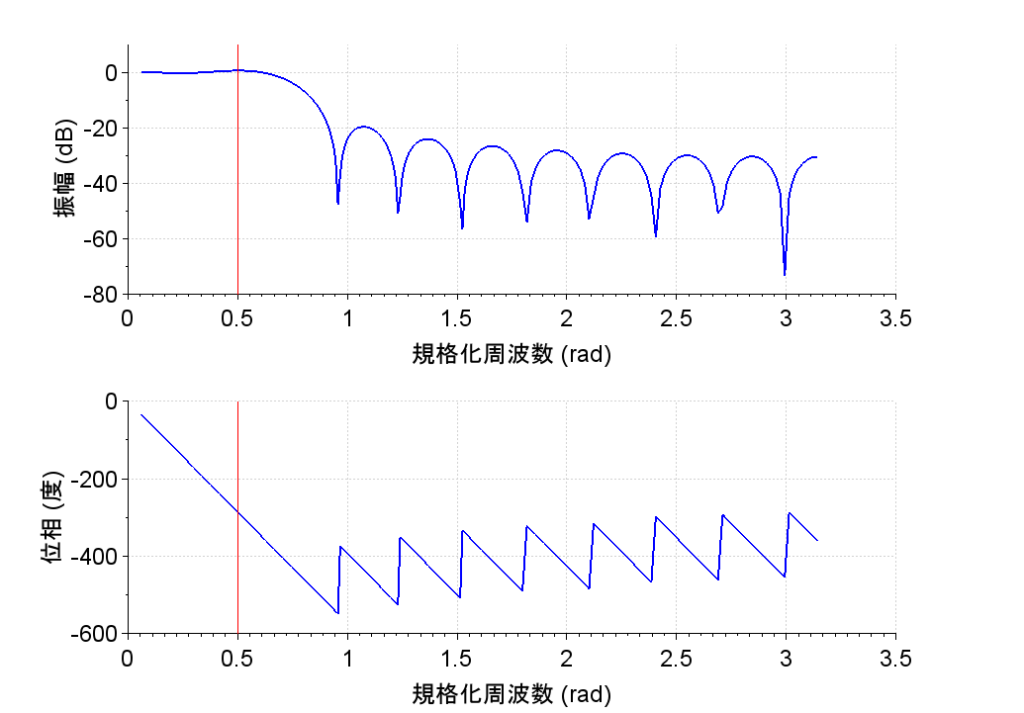
\(N=\pm10\)の場合
窓関数法
理想低域フィルタのインパルス応答列を途中で打ち切りFIRフィルタを実装した場合、図4の周波数特性に見られるようにリップル(変動)や遮断周波数(\(\Omega_c =\pi/4\))近傍の減衰性の劣化が見られる。図3の例では、インパルス応答列を\(N=\pm 10\)で打ち切ったが、打ち切り範囲を\(N=\pm 100\)まで広げると、図5のようになる。このインパルス応答列を元に低域FIRフィルタを構成して、周波数特性を求めると図6のようになる。このようにインパルス応答列の範囲を広げることで、周波数特性の遮断周波数(\(\Omega_c =\pi/4\))近傍では、理想LPFの特性に近くなる。しかし、この方法では演算量が多くなり実装が難しくなる。例えば、図6の例では係数との乗算だけで200回必要となり、さらに加算も必要となる。そこで、無限に続くインパルス応答を打ち切る際に、適当な重み関数\(w(n)\)を掛けると遮断周波数近傍におけるリップルを抑えることができる。この重み関数を用いるFIRフィルタの設計法を窓関数法という。窓関数の関数形の例を表2に示す。
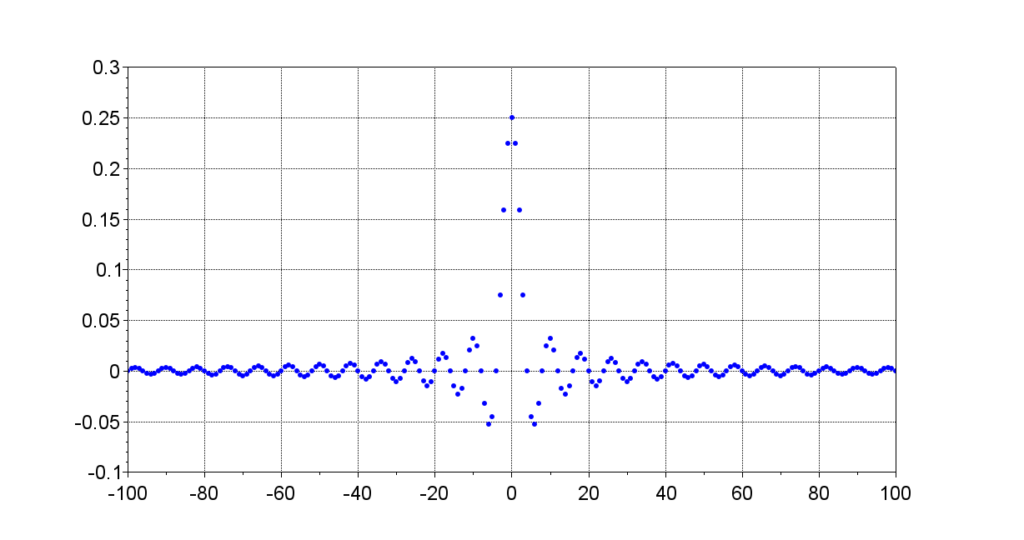
\(N=\pm 100\)の場合
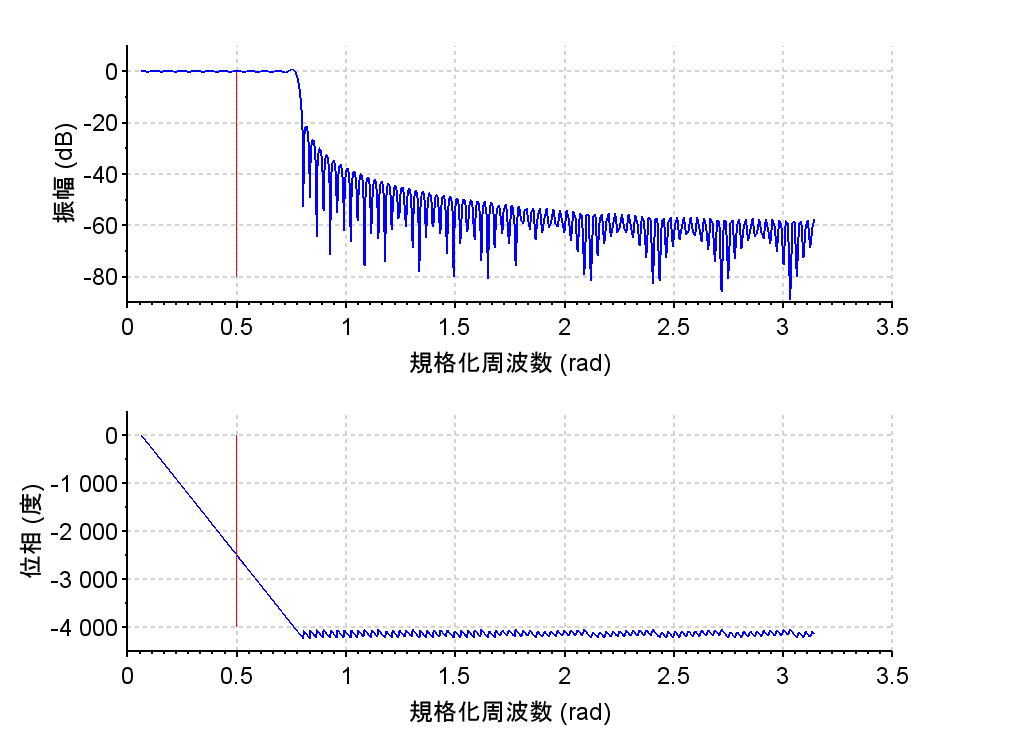
\(N=\pm100\)の場合
| 名前 | 関数形 |
| 方形窓 | \(w(k)=1 , \;\;\;(0 \leq k \leq M)\) |
| Hanning窓 | \(w(k) = \frac{1}{2}\left[ 1- \cos\left(\frac{2 \pi k}{M} \right) \right] \;\;\;(0 \leq k \leq M)\) |
| Hamming窓 | \(w(k) = 0.54 - 0.46 \cos \left(\frac{2\pi k}{M}\right) \;\;\; (0 \leq k \leq M)\) |
| Blackman窓 | \(w(k) = 0.42 - 0.5 \cos \left(\frac{2 \pi k}{M} \right) + 0.08 \cos\left(\frac{4 \pi k}{M} \right) \;\;\; (0 \leq k \leq M)\) |
| Kaiser窓 | \(w(k) = \frac{I_0 \left[\alpha \sqrt{1- (1 - 2k/M)^2}\right] }{I_0 [\alpha]} \;\;\; (0 \leq k \leq M, 4 <\alpha < 9) \\ I_0[\alpha] \simeq 1+ \sum_{l=1}^{L} \left(\frac{(\alpha /2)^l}{l !}\right)^2 \;\;\;(L は15程度)\) |
図7は、\(M=20\)としたときのHanning窓、Hamming窓、Blackman窓の形状である。
適当な窓関数を理想低域フィルタのインパルス応答に掛け合わせることにより、打ち切りの影響を低減する。なお、時間領域の積のフーリエ変換は、周波数領域では畳み込みの関係となる。
図8は、図3のインパルス応答列にHanning窓を掛けた結果である。図9は、Hanning窓を掛けた場合の周波数特性である。図10は、Hamming窓を掛けた場合の周波数特性である。図11は、Blackman窓を掛けた場合の周波数特性である。いずれも図3と比較してリップルが減少していることがわかる。遮断特性を改善するには、\(N\)を増やす必要があるが、窓を適切に掛けることにより、リップルを減少させることができる。Scilabスクリプトを下記に示すので、各種の窓の効果、打ち切り範囲による効果を試して欲しい。
Scilabスクリプト(窓関数法)
//窓関数
clear; clf();
pi=%pi; z=%z;
M=50;
k=0:1:M;
//Hanning
w1=(1/2)*(1-cos((2*pi*k)/M));
//Hamming
w2=0.54-0.46*cos((2*pi*k)/M);
//Blackman
w3=0.42-0.5cos*((2*pi*k)/M) + 0.08*cos((4*pi*k)/M);
scf(0); plot(k, [w1' w2' w3'],'.');
L=200; N=M/2;
//理想LPFのインパルス応答
n=-L:1:L;
h=(1/4)*sinc(n*pi/4);
scf(1); plot(n,h,'.');
//インパルス応答の打ち切り
n=-N:1:N;
h=(1/4)*sinc(n*pi/4);
scf(2); plot(n,h,'.');
//インパルス応答のシフト(FIRフィルタの係数計算)
n=n+N;
scf(3);plot(n,h,'.');
//窓関数とインパルス応答の積
wh=w1.*h;//適当な窓関数を選択する
scf(4); plot(n,wh,'.');
T=1;
//窓関数を適用したFIRフィルタの伝達関数
Hz = wh(1);
for n=1:M,
Hz = Hz + wh(n+1).*z^-n;
end;
//システム関数に変換
Hzz=syslin(T,Hz);
//ボード線図の描画
scf(5); bode(Hzz,0.01,4,'rad');
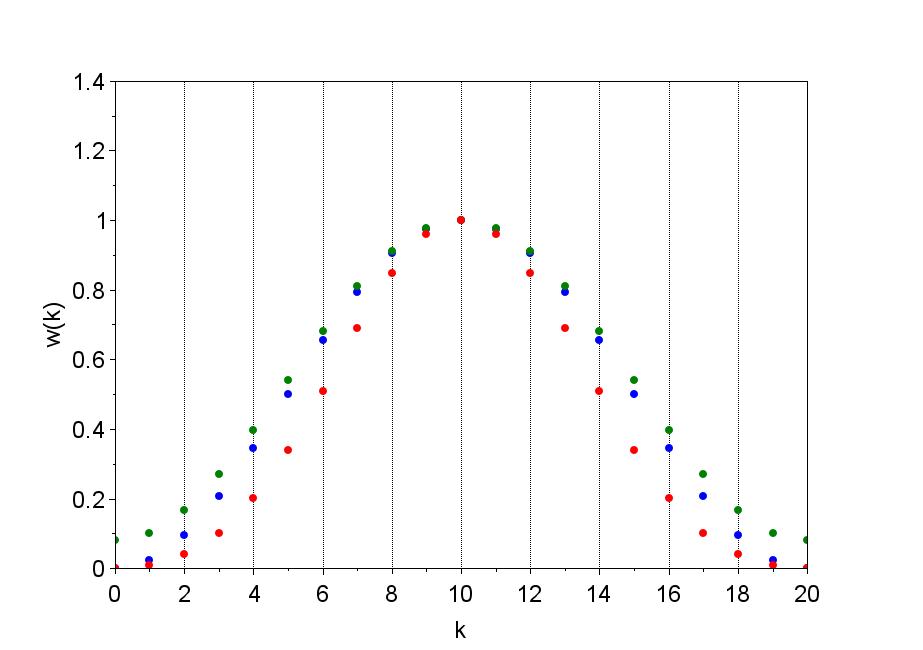
赤:Blackman、青:Hanning、緑:Hamming
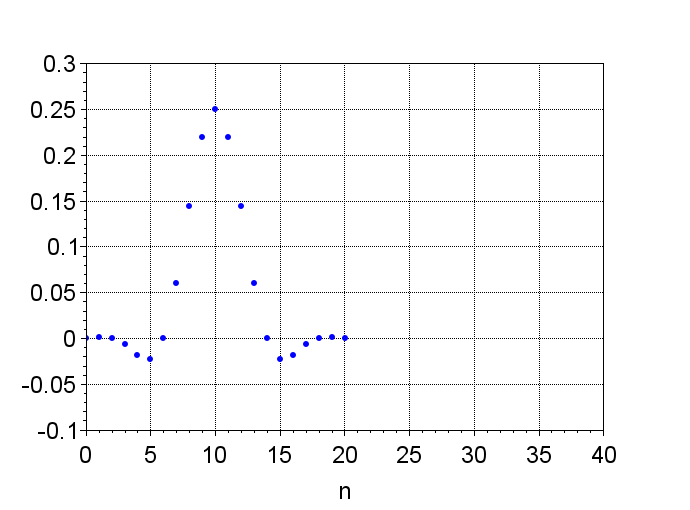
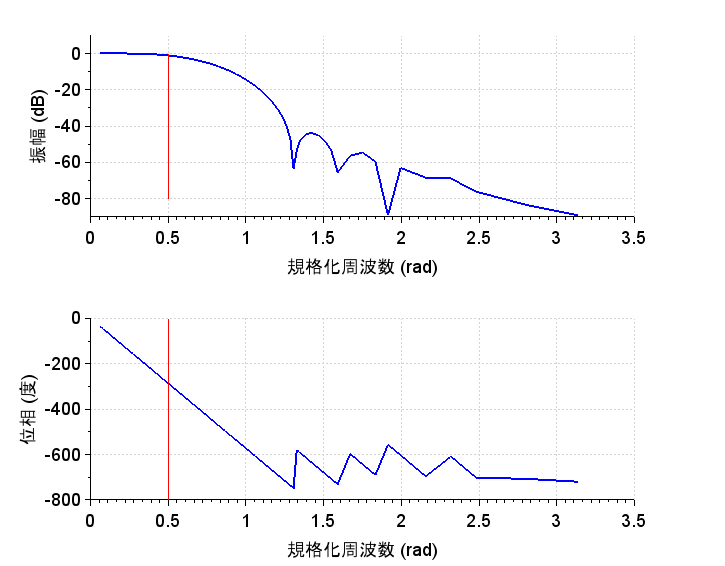
FIR LPFフィルタ周波数特性
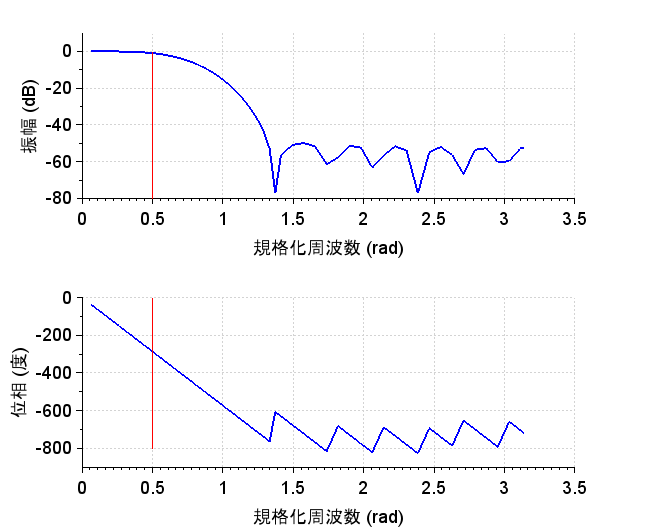
FIR LPFフィルタ周波数特性
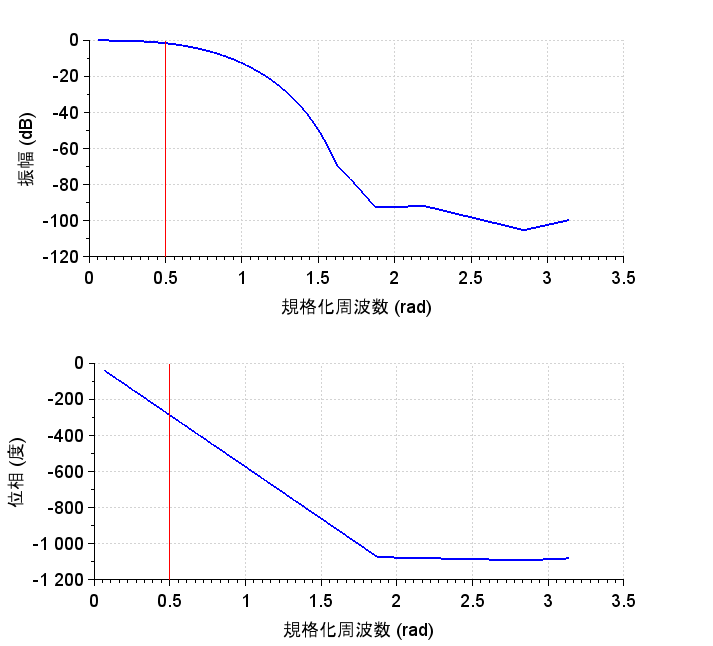
FIR LPFフィルタ周波数特性