1. 静電力
静電力は、帯電した物体同士に働く力である。帯電とは、物体に電荷と呼ばれる電気的な状態が蓄積されることを指す。電荷には正と負があり、同じ極性の電荷は反発し合い、異なる極性の電荷は引き付け合う。静電力は、私たちの身の回りで様々な現象を引き起こしている。例えば、静電気ショック(帯電した物体に触れたときに感じるバチッという衝撃)、雷(雲の中で発生した静電気が放電される現象)、埃の付着( ホコリは静電気を帯びやすく、そのため物体に付着しやすくなる)などがある。
電荷
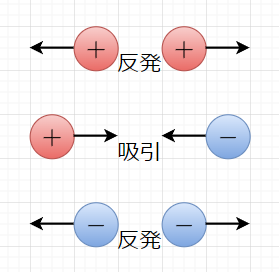
物質は原子で構成されており、物質を構成する原子は、便宜上、図1のような原子模型(太陽系モデル)で表すことができる。原子は、原子核と電子からなり、原子核は正の電荷をもつ陽子と電荷をもたない中性子からなる。電子は負の電荷をもち、通常は原子の種類で定まる数だけ原子核の周りにあり、原子核の周りの定まった軌道を回っていると見なせる。原子の通常状態では、陽子がもつ正電荷の総量と電子のもつ負電荷の総量の絶対値は等しいので原子を外部から見ると、正電荷と負電荷の性質が打ち消されて、見かけ上、電気的に中性となり、原子の外部には電気的性質を示さない。電荷間に働く力は、図2に示すように、正電荷同士、負電荷電子は反発し、正電荷と負電荷は吸引する。従って、原子内では、負電荷をもつ電子は、正電荷をもつ陽子との吸引力により、原子核に束縛されている。しかし、原子核から最も外側の軌道を回る電子は、原子核からの吸引力が弱いため、外部からの摩擦力や熱などのエネルギーが加わると、電子は原子から離脱する。原子から離脱した電子は、物質内を移動したり、その物質から離れて他の物質に移動したりする。このように原子核の束縛から離れた電子を自由電子という。電子が離れた物質(原子)では、陽子のもつ正電荷が相対的に多くなったことになる。この物質の状態を正に帯電したという。一方、電子が移動した物質側では負の電荷が多くなるので、負に帯電することになる。
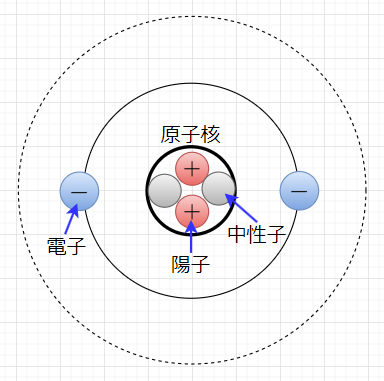
(太陽系モデル)
電荷の単位とクーロン力
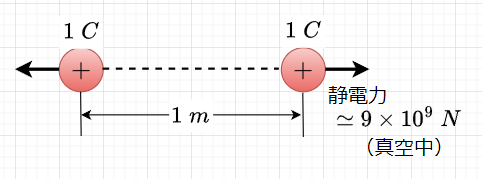
電荷(電気量)の単位には、クーロン[\(C\)]を用いる。\(1 \; C\)を静電力で表すと、図3のように同じ大きさの電荷を真空中に\(1\; m\)離して置いたとき、この電荷間に約\(9 \times 10^9 \;N\)の静電力が働くときの電荷の大きさが\(1\;C\)である。
電子の電荷量は、\(e\)と書き、\(e= -1.60217663 \times 10^{-19} \;C\)である。これが現在知られている最も小さい帯電体で、この絶対値を電気素量と言う。電流の単位\([A]\)において、\(1\;A\)は、\(1\;s\)間に\(1 \;C\)の電荷が通過することを意味しているので、電子は \(1\; s\)間に\(\frac{1}{1.60217663 \times 10^{-19}} \simeq 6.24 \times 10^{18} \)個通過することになる。なお、電子を粒子として扱う場合の電子の質量\(m\)は、\(m = 9.1093837 \times 10^{-31} \;kg\)である。
クーロンの法則
2つの電荷間に働く静電力の大きさは、2つの電荷量の積に比例し、2つの電荷間の距離の2乗に反比例する。
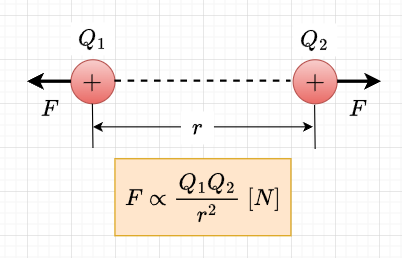
電荷間に働く力(反発力、または、吸引力)を静電力と呼ぶが、この力はクーロンの法則に従う。図4に示すように、2つの電荷量を\(Q_1\;[C],\; Q_2\;[C]\)、電荷間の距離を\(r\;[m]\)、静電力を\(F\;[N]\)とすると、$$F \propto \frac{Q_1 Q_2}{r^2}$$が成り立つ。国際単位系で記述すると、比例定数を\(k\)として、$$F = k \frac{Q_1 Q_2}{r^2} \;\;[N]$$と書ける。比例定数\(k\)は、$$k=\frac{1}{4 \pi \epsilon_0} = 9 \times 10^9$$である。ここで、\(\epsilon_0\)は真空の誘電率で、\(\epsilon_0 = 8.855 \times 10^{-12}\;\;[F/m]\)である。
真空以外で一般の媒質中の場合は、一般に静電力は弱くなる。この場合、真空の誘電率の代わりに誘電率\(\epsilon\)を用いる。さらに、比誘電率\(\epsilon_s = \frac{\epsilon}{\epsilon_0}\)を定義し、\(\epsilon = \epsilon_s \epsilon_0\)と表す。従って、一般の媒質中におけるクーロンの法則は、$$F = \frac{1}{4 \pi \epsilon_0 \epsilon_s} \frac{Q_1 Q_2}{r^2} \;\;[N]$$となる。比誘電率は、空気で\(1.00059\)、水で\(80.4\)程度で、比誘電率の大きい物質では\(5,000\)を越える。従って、媒質中のクーロン力は、真空中に比べて小さくなる。