14. 状態フィードバック
状態フィードバック(state feedback)とは、制御対象の状態変数を測定して、その情報を元に制御入力を決定する方法である。制御対象の状態変数とは、制御対象の内部状態のことであり、その状態変数を観測することで、制御対象の現在の状態を正確に知ることができる。状態フィードバックでは、制御対象の状態変数を基にフィードバック制御系の状態フィードバックゲインを用いて、制御入力を決定する。この制御入力は、制御対象の状態変数を目標値に近づけるように設計する。状態フィードバックは、制御対象が線形である場合に最も効果的な手法の1つである。状態フィードバックは、多くの制御システムに応用されており、飛行機のオートパイロット、自動車の制御システム、産業ロボットの制御システムなどに使用されている。
\((\boldsymbol{A, \; B})\)が可制御である、\(m\)入力の制御対象$$\boldsymbol{\dot{x}}(t) = \boldsymbol{Ax}(t) + \boldsymbol{Bu}(t) \; \cdots \; (1)\\ \boldsymbol{A}(n \times n), \; \;\boldsymbol{B}(n \times m)$$において、状態変数\(x_1(t), \cdots, x_n(t)\)が直接観測可能と仮定し、制御入力を$$\boldsymbol{u}(t) = - \boldsymbol{Fx}(t)\; \cdots\;(2)$$とする。これを状態フィードバック制御という。構成は、図「状態フィードバック」のようになる。
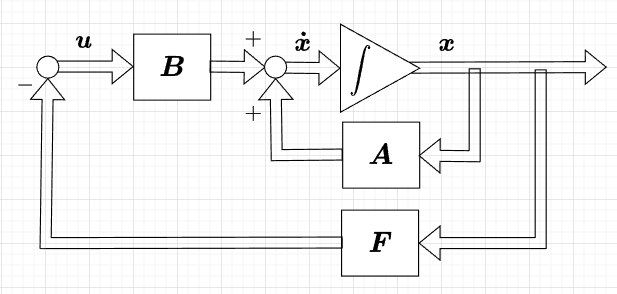
レギュレータ
ただし、$$\boldsymbol{F} = \begin{bmatrix} f_{11} & f_{12} & \cdots & f_{1n} \\ \vdots & \vdots & & \vdots \\ f_{m1} & f_{ms} & \cdots & f_{mn} \end{bmatrix} \;\;\;\;\; (m \times n)$$と選ぶ。\(\boldsymbol{F}\)をフィードバック係数行列という。とくに、1入力(\(m=1\))で、\(\boldsymbol{B} = \boldsymbol{b} \;(n \times 1)\)となるときは、\(\boldsymbol{F}\)は行ベクトル$$\boldsymbol{f} = \begin{bmatrix} f_1 & f_2 & \cdots & f_n \end{bmatrix} \;\;\;(1 \times n)$$となり、フィードバック係数ベクトルという。
式(2)を式(1)へ代入すると、$$\boldsymbol{\dot{x}}(t) = (\boldsymbol{A} - \boldsymbol{BF})\boldsymbol{x}(t) \; \cdots \; (3)$$となる。制御前のシステム 式(1)を開ループシステム、制御後のシステム 式(2)を閉ループシステムと呼ぶ。
式(3)の解は、$$\boldsymbol{x}(t) = \mathrm{exp}[(\boldsymbol{A} - \boldsymbol{BF})t]\cdot \boldsymbol{x}(0)$$となる。ここで、\(\boldsymbol{x}(0)\)は初期外乱で原点\(\boldsymbol{0}\)(平衡点)からずれた\(t=0\)での初期ベクトルを表す。よって、\(\boldsymbol{F}\)を選んで、\(\boldsymbol{A-BF}\)が安定行列にできれば、すべての\(\boldsymbol{x}(0) \neq \boldsymbol{0}\)に対して、\(\boldsymbol{x}(t) \rightarrow \boldsymbol{0} \; (t \rightarrow \infty)\)となり、状態変数を漸近的に原点へ戻すことができる。この閉ループシステムをレギュレータという。また、\(\boldsymbol{A-BF}\)の固有値をレギュレータの極という。
\(\boldsymbol{A-bf}\)の固有値の設定
1入力システムでのフィードバック係数ベクトルを決定する手順を以下に示す。(多入力システムの場合は、複雑になるので参考文献などを参照して欲しい。)
・\(\boldsymbol{A}\)の特性方程式、$$|s \boldsymbol{I} - \boldsymbol{A}| = s^n + a_n s^{n-1} + \cdots + a_2 s + a_1$$と可制御性行列\(\boldsymbol{U}_c\)を求め、可制御正準形式への変換行列\(\boldsymbol{T}\)をつくる。
・配置したい極\(\mu_1 \sim \mu_n\)から、$$(s - \mu_1)(s - \mu_2) \cdots (s - \mu_n) = s^n + \alpha_n s^{n-1} + \cdots + \alpha_2 s + \alpha_1$$として、\(\boldsymbol{A-bf}\)が満たすべき特性多項式の係数\(d_1 \sim d_n\)を求める。
・以上より、\(\boldsymbol{f}\)は、$$\boldsymbol{f} = \begin{bmatrix} \alpha_1 - a_1 & \alpha_2 - a_2 & \cdots & \alpha_n - a_n \end{bmatrix} \boldsymbol{T}^{-1}$$として、フィードバック係数が唯一に定まる。
レギュレータの極配置【例】
1入力システムを$$\boldsymbol{\dot{x}} = \begin{bmatrix} -4 & 2 & 0 \\ 1 & -3 & 1 \\ 0 & 1 & -2\end{bmatrix} \boldsymbol{x} + \begin{bmatrix} 2 \\ 0 \\ 0 \end{bmatrix} u $$とする。このシステムの固有値は、
である。速応性を得るため、極を\(\mu_1,\mu_2 = -5 \pm j2 ,\;\; \mu_3 = -6\)に設定する。このときのフィードバック係数ベクトル\(\boldsymbol{f}\)を求める。
Scilabのスクリプトで求めた結果を示す。
--> evals //制御対象の固有値
evals =
-5.1149075 + 0.i
-2.7458983 + 0.i
-1.1391941 + 0.i
--> n //可制御性行列のランク
n =3.
--> f //フィードバック係数ベクトル
f =3.5 15.5 30.5
--> cpoles //極配置の確認
cpoles =
-6. + 0.i
-5. + 2.i
-5. - 2.i
Scilabスクリプト【例】
//状態フィードバック(レギュレータ)
clear; clf(); i=%i;
//制御対象の定義
A=[-4 2 0; 1 -3 1; 0 1 -2]; b=[2; 0; 0]; c=[1 0 0; 0 1 0; 0 0 1];
sysP=syslin('c',A,b,c);
//制御対象の固有値
evals=spec(A);
//可制御性のチェック
Cc=cont_mat(A,b); n=rank(Cc);
//極配置
poles=[-5+i*2 -5-i*2 -6];
//状態フィードバック係数の決定
f=ppol(A,b,poles);
cpoles=spec(A-b*f); //極配置の確認
//制御対象のインパルス応答
t=0:0.01:2;
y0=csim('impulse',t,sysP);
scf(0); plot(t',y0');
//レギュレータのインパルス応答
A2=A-b*f;
sysP2=syslin('c',A2,b,c);
y=csim('impulse',t,sysP2);
scf(1); plot(t',y');
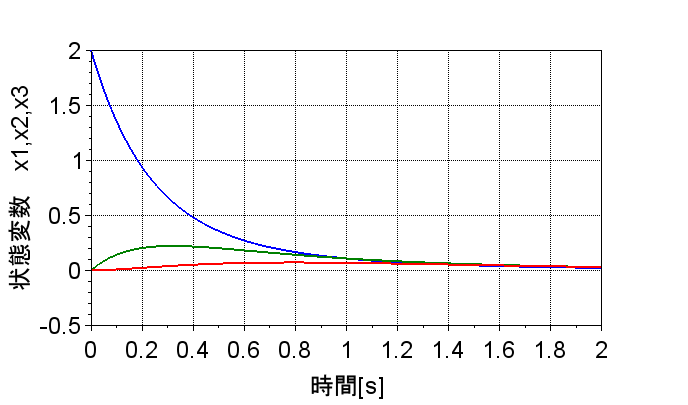
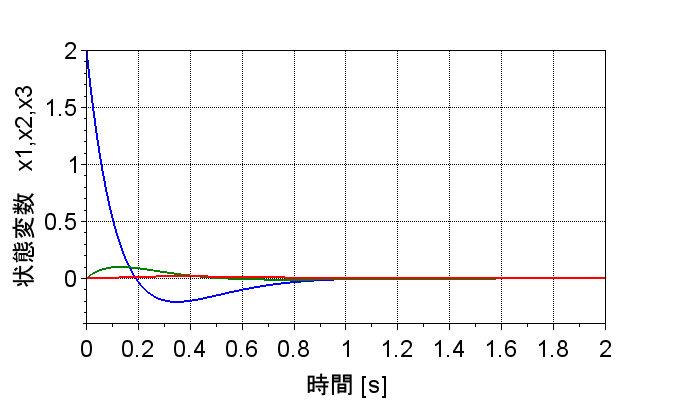
制御対象のインパルス応答と状態フィードバック後のレギュレータのインパルス応答を比較すると、レギュレータのインパルス応答の方が速応性が改善されており、速く零に収束している。これは制御対象の固有値に虚軸に近い固有値があることからも分かる。


“14. 状態フィードバック” に対して1件のコメントがあります。
コメントは受け付けていません。