12. 可制御正準形
可制御正準形(Controllable Canonical Form)とは、状態空間表現を可制御性に関する正準形に変換することで、制御系の解析や設計を容易にする手法である。
状態空間表現は、状態方程式と出力方程式によって構成される。可制御性とは、系の全状態を初期状態から有限時間内に任意の状態に到達できる能力のことを指す。可制御性がある場合、制御器を設計して所望の状態に制御できることが保証される。また、可制御正準形に変換することで、制御系の解析に必要な情報が明確になる。
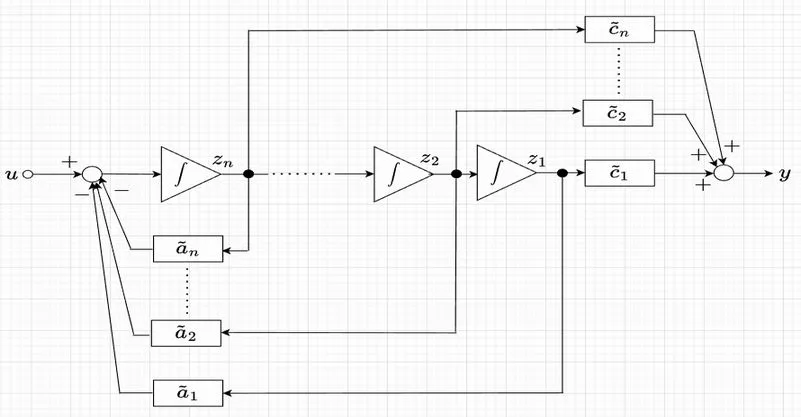
\((\boldsymbol{A, b}) \)が可制御な1入力システムにおいて、\(\boldsymbol{A}\)の特性多項式が$$|s \boldsymbol{I} - \boldsymbol{A} | = s^n + a_n s^{n-1} + \cdots + a_2 s +a_1$$であるとき、$$\boldsymbol{T} = \boldsymbol{U}_c \boldsymbol{W} =\begin{bmatrix} \boldsymbol{b} & \boldsymbol{Ab} & \cdots & \boldsymbol{A^{n-1} b} \end{bmatrix} \begin{bmatrix} a_2 & a_3 & a_4 & \cdots & \cdots & a_n & 1 \\ a_3 & a_4 & \cdots &\cdots & a_n & 1 & \\a_4 & \cdots & \cdots & a_n & 1 & & \\ \vdots & \cdots & \cdots & & & \\ a_n & 1 & & \boldsymbol{0} & & & \\ 1 & & & & & &\end{bmatrix}$$の変換行列をつくる。これにより、\(\boldsymbol{x}(t) = \boldsymbol{Tz}(t)\)の変換によって、\(\boldsymbol{\tilde{A}}, \; \boldsymbol{\tilde{b}}\)が可制御正準形式の$$\boldsymbol{\tilde{A}} = \boldsymbol{T}^{-1} \boldsymbol{A} \boldsymbol{T} = \begin{bmatrix} 0 & 1 & 0 & \cdots & 0 \\ \vdots & \ddots & 1 & \ddots & \vdots \\ \vdots & & \ddots & \ddots & 0 \\0 &\cdots & \cdots & 0 & 1 \\-a_1 & -a_2 & \cdots & \cdots & -a_n \end{bmatrix} ,\; \boldsymbol{\tilde{b}} = \boldsymbol{T}^{-1} \boldsymbol{b} = \begin{bmatrix} 0 \\ \vdots \\ \vdots \\0 \\ 1 \end{bmatrix}$$となる。さらに、$$\boldsymbol{\tilde{c}} = \boldsymbol{cT} = \begin{bmatrix} \tilde{c}_1 & \tilde{c}_2 & \cdots & \tilde{c}_n \end{bmatrix}$$とすると、可制御正準形システムは、$$\begin{bmatrix} \dot{z}_1 \\ \dot{z}_2 \\ \vdots \\ \dot{z}_n \end{bmatrix} = \begin{bmatrix} 0 & 1 & 0 & \cdots & 0 \\ \vdots & \ddots & 1 & \ddots & \vdots \\ \vdots & & \ddots & \ddots & 0 \\0 &\cdots & \cdots & 0 & 1 \\-a_1 & -a_2 & \cdots & \cdots & -a_n \end{bmatrix} \begin{bmatrix} z_1 \\ z_2 \\ \vdots \\ z_n \end{bmatrix} + \begin{bmatrix} 0 \\ \vdots \\ 0 \\1 \end{bmatrix} u $$ $$ y = \begin{bmatrix} \tilde{c}_1 & \tilde{c}_2 & \cdots & \tilde{c}_n \end{bmatrix} \begin{bmatrix} z_1 \\ z_2 \\ \vdots \\ z_n \end{bmatrix}$$となる。この式から、図「可制御正準形システム」が描ける。
このとき、伝達関数は、$$\boldsymbol{G}(s) = \boldsymbol{c} (s\boldsymbol{I} - \boldsymbol{A})^{-1} \boldsymbol{b} = \boldsymbol{\tilde{c}}(s\boldsymbol{I} - \boldsymbol{\tilde{A}})^{-1} \boldsymbol{\tilde{b}} \\=\frac{\tilde{c}_n s^{n-1} + \tilde{c}_{n-1} s^{n-2} + \cdots + \tilde{c}_2 s + \tilde{c}_1} {s^n + a_n s^{n-1} + \cdots + a_2 s + a_1}$$となり、そのパラメータは正準システムのパラメータと1対1に対応している。
また、 \(\boldsymbol{\tilde{A}}\)の第\(n\)行目の要素の符号を反転したものが、特性多項式の係数となる。


“12. 可制御正準形” に対して2件のコメントがあります。
コメントは受け付けていません。