18. システムの周波数応答

フーリエ解析が示すように、多くの時間信号はさまざまな周波数の正弦波成分に分解できる。システムの周波数応答では、この考え方に基づき動的システムの入出力信号の正弦波成分を抽出して、動的システムの 特徴を捉えることを考える。これを周波数領域解析という。（これに対してインパルス応答やステップ応答などは時間領域解析という。）
動的システムの特性を捉える計測手法として、周波数応答法がある。これは、動的システムに正弦波信号（正弦波状の外力なども含む）を入力し、その出力を測定する方法である。線形システムでは、出力信号は入力信号の正弦波と同一周波数で、位相と振幅が異なるという特徴がある。

正弦波を入力とした時の出力

入力\(u(t)=A\sin\omega t\)とする。（位相\(\theta=0\)とした正弦波信号）　この信号を入力するシステムは安定であり、伝達関数\(G(s)\)は以下とする。$$G(s)=\frac{ b_ms^m+b_{m-1}s^{m-1}+\cdots+b_1s+b_0 }{ (s-p_1)(s-p_2)\cdots(s-p_n) } \enspace \enspace (n\ge m)$$入力\(u(t)\)のラプラス変換は、\(U(s)=\mathcal{L}\{u(t)\}=\frac{A\omega}{s^2+\omega^2}\)なので、出力\(Y(s)\)は、$$Y(s)=G(s)U(s)=G(s)\frac{A\omega}{(s+j\omega)(s-j\omega)}$$となる。ここで、\(\frac{A\omega}{(s+j\omega)(s-j\omega)}\)の部分は次のように部分分数展開できる。$$G(s)\frac{A\omega}{(s+j\omega)(s-j\omega)}$$ $$=\frac{\alpha}{s+j\omega}+\frac{\beta}{s-j\omega}$$ $$=\frac{\alpha(s-j\omega)+\beta(s+j\omega)}{(s+j\omega)(s-j\omega)}$$　なお、\(\alpha=\frac{AG(-j\omega)}{-2j} \enspace, \enspace \beta=\frac{AG(j\omega)}{2j} \) 　となる。
（ \(G(s)A\omega=\alpha(s-j\omega)+\beta(s+j\omega)\)を成立させるために、両辺に\(s=j\omega\)を代入して\(\alpha\)を求め、\(s=-j\omega\)を代入して\(\beta\)を求める。）\(G(s)\)も部分分数展開すると出力\(Y(s)\)は、
$$Y(s)=\frac{\alpha}{s+j\omega}+\frac{\beta}{s-j\omega}+\sum^n_{i=1}\frac{c_i}{s-p_i}$$ $$=A\left|G(j\omega)\right|\left(\frac{e^{j\phi}}{2j(s-j\omega)}+\frac{e^{-j\phi}}{-2j(s+j\omega)}\right)$$ $$+\sum^n_{i=1}\frac{c_i}{s-p_i}$$となる。ここで、\(G(j\omega)=\left|G(j\omega)\right|e^{j\phi}\) , \(G(-j\omega)=\left|G(j\omega)\right|e^{-j\phi}\) , \(\phi=\arg G(j\omega)\)
従って、\(y(t)\)は$$y(t)=\mathcal{L}^{-1}\{Y(s)\}$$ $$=A\left|G(j\omega)\right|\left( \frac{e^{j\phi}e^{j\omega t}-e^{-j\phi}e^{-j\omega t}}{2j}\right)$$ $$+\sum^n_{i=1}c_ie^{p_i t}$$となる。整理すると、$$y(t)=A\left|G(j\omega)\right|\sin(\omega t+\phi)+\sum^n_{i=1}c_ie^{p_i t}$$ と表せる。\(\sum^n_{i=1}c_ie^{p_i t}\)の部分は、\(G(s)\)が安定なので\(p_i\)の実部は負であり、この項は十分に時間がたつと０に収束する。従って、そのときの出力は、$$y(t)=A\left|G(j\omega)\right|\sin(\omega t+\phi)$$ $$=A\left|G(j\omega)\right|\sin(\omega t+\arg G(j\omega))$$ となる。以上より、角周波数\(\omega\)の正弦波信号を線形で安定な動的システムに入力したとき、その出力は入力と同じ周波数\(\omega\)の正弦波信号となることが分かる。また、その時の出力の振幅は入力の振幅\(A\)の\(\left|G(j\omega)\right|\)倍、位相は\(\phi=\arg G(j\omega\))に変化し、それらの値は\(\omega\)の関数になっている。位相\(\phi\)が正なら入力信号に比べて出力信号は位相が進み、負ならば位相が遅れることになる。

周波数伝達関数

伝達関数が\(G(s)\)のとき、\(s\rightarrow j\omega\)とすると、周波数伝達関数\(G(j\omega)\)が求まる。\(G(j\omega)\)は複素関数なので、$$G(j\omega)=a(\omega)+jb(\omega)$$ $$=Re\{G(j\omega)\}+jIm\{G(j\omega)\}$$と表せる。従って、$$\left|G(j\omega)\right|=\sqrt{a^2(\omega)+b^2(\omega)} ,$$ $$\arg{G(j\omega)}=\tan^{-1}\frac{b(\omega)}{a(\omega)}$$となる。

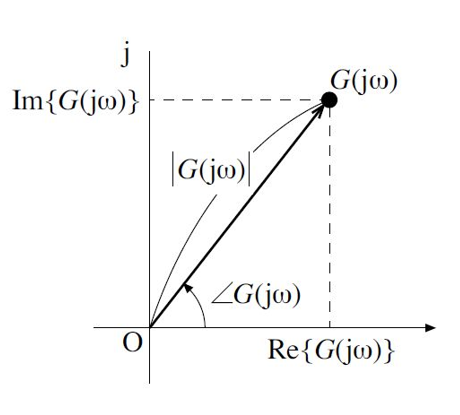
$$a(\omega)=Re\{G(j\omega)\} ,$$ $$b(\omega)=Im\{G(j\omega)\}$$ ( \( \arg{G(j\omega)} \) は \( \angle{G(j\omega)} \)とも書く。）
直交形式：\(G(j\omega)=Re\{G(j\omega)\}+jIm\{G(j\omega)\}\)
極座標形式：\(G(j\omega)=\left|G(j\omega)\right|\angle{G(j\omega)}=\left|G(j\omega)\right|e^{j\angle{G(j\omega)}} \)
\( \phi=\arg{G(j\omega}) \)とすると、$$G(j\omega)=a(\omega)+jb(\omega)$$ $$=\left|G(j\omega)\right|\left(\cos\phi + j\sin\phi\right)$$ $$G(j\omega)=\left|G(j\omega)\right|e^{j\phi} $$　このように様々な表現形式があるが、複素平面のイメージを意識すれば読み惑うことはない。