19. ボード線図
周波数伝達関数\(G(j\omega)\)の図式表現の一つにボード線図がある。周波数伝達関数\(G(j\omega)\)は、$$G(j\omega)=a(\omega)+jb(\omega)=\left|G(j\omega)\right|e^{j\phi} ,$$ $$ \phi=\arg{G(j\omega)}$$と表せてゲインと位相は、$$\left|G(j\omega)\right|=\sqrt{a^2(\omega) + b^2(\omega) } $$ $$\phi(\omega)=\arg G(j\omega)=\tan^{-1}\left\{\frac{b(\omega)}{a(\omega)}\right\}$$となり、\(\left|G(j\omega)\right| ,\phi(\omega) \)は\(\omega\)の関数となる。\(\left|G(j\omega)\right|\)を利得特性、\( \phi(\omega)\)を位相特性と呼ぶ。
ボード線図では、ゲイン線図とよばれるゲイン(利得)ー周波数特性と、位相線図と呼ばれる位相ー周波数特性を別々のグラフで描く。周波数伝達関数は\(G(j\omega)=\left|G(j\omega)\right|e^{j\phi} \)とゲインと位相が一つの式で表されるが、ボード線図で描くことにより、周波数とゲインの関係、周波数と位相の関係が読み取りやすくなる。
ボード線図の描画は、実践的には例に示すようにScilabやMatlabなどのソフトウェアを使用して正確に描く。また、Pythonなどを使ってプログラムで描くことも容易にできる。しかし、システムの振る舞いをおおよそ把握するには、後に示す基本要素のボード線図の概形を憶えておくのは有用である。
| 1000倍 | 60dB | \(\frac{1}{\sqrt2}\)倍 | \(-3\)dB |
| 100倍 | 40dB | \(\frac{1}{2}\)倍 | \(-6\)dB |
| 10倍 | 20dB | \(\frac{1}{10}\)倍 | \(-20\)dB |
| 2倍 | 6dB | \(\frac{1}{100}\)倍 | \(-40\)dB |
| \(\sqrt2\)倍 | 3dB | \(\frac{1}{1000}\)倍 | \(-60\)dB |
| 1倍 | 0dB | | |
ゲイン線図では、横軸を角周波数\(\omega\)(または、周波数\(f\))の対数目盛にとる。\(\omega\)(または、\(f\))が10倍になる間隔を1デカート[dec]とよぶ。縦軸はゲインをとるが、\(g=20\log_{10}\left|G(j\omega)\right|\)[dB] とデシベルに変換して用いることが多い。(なお\(\log\)の底を10とした常用対数を使う。)デシベル表示では、ゲインが1倍(入出力の振幅の比が1)ならば\(0\)[dB]、10倍なら\(20\)[dB]、1/10倍なら\(-20\)[dB]となる。
位相線図では、横軸をゲイン線図と同様に角周波数\(\omega\)(または、周波数\(f\))の対数目盛にとり、縦軸を位相角にとる。単位は度[deg]とする([rad]にとる場合もある)。
ゲイン、位相の計算
入力 \(u(t)\)と出力\(y(t)\) のラプラス変換をそれぞれ\(U(s)\)、\(Y(s)\) とおくと、伝達関数は$$G(s)=\frac{Y(s)}{U(s)}$$となる。ここで、\(s\rightarrow j\omega_0\)とすると、角周波数\(\omega = \omega_0\)における周波数応答\(G(j \omega_0)\)に関して次の関係式が成り立つ。$$G(j \omega_0)=\frac{Y(j \omega_0)}{U(j \omega_0)}$$従って、そのゲイン(大きさ)と位相(偏角)は、$$\left|G(j \omega_0)\right|=\left|\frac{Y(j \omega_0)}{U(j\omega_0)}\right|$$ $$=\frac{\left|Y(j \omega_0)\right|}{\left|U(j \omega_0)\right|}$$ $$\angle{G(j \omega_0)}=\angle \left(\frac{Y(j\omega_0)}{U(j \omega_0)}\right)$$ $$=\angle{Y(j \omega_0)}-\angle{U(j \omega_0)}$$となる。
[例]
\(z=\frac{1}{x+jy}\)ならば、\( \left|z\right|=\frac{1}{\sqrt{x^2+y^2}} \)であり、$$\angle{z}=\tan^{-1}\left(\frac{0}{1}\right)-\tan^{-1}\left(\frac{y}{x}\right)$$ $$=0\text{°}-\tan^{-1}\left(\frac{y}{x}\right)$$ $$=-\tan^{-1}\left(\frac{y}{x}\right)$$となる。
積分要素のボード線図
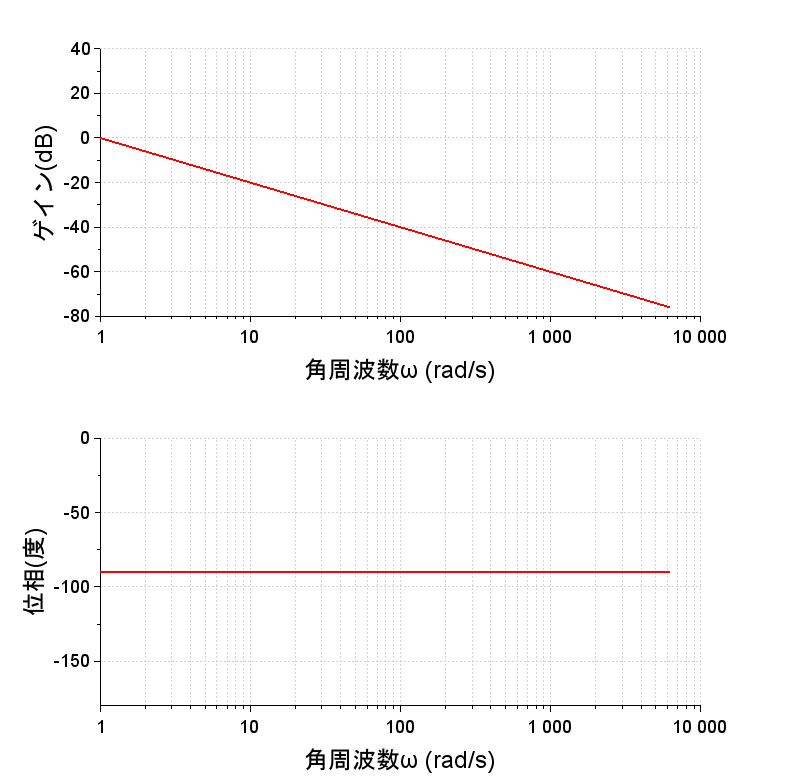
積分要素\( G(s)=\frac{1}{s} \)は$$G(j\omega)=\frac{1}{j\omega}=-\frac{j}{\omega}$$なのでゲインは、$$g=20\log\left|-\frac{j}{\omega}\right|=20\log\left(\frac{1}{\omega}\right)$$ $$=-20\log\omega [dB]$$であり、位相は、\( \arg G(j\omega)=-90\text{°} \)となる。ゲインは\(-20dB/dec \)で低下し、位相は角周波数によらず\(90\text°\)遅れ(\(-90\text°\))となる。
一次遅れ要素のボード線図
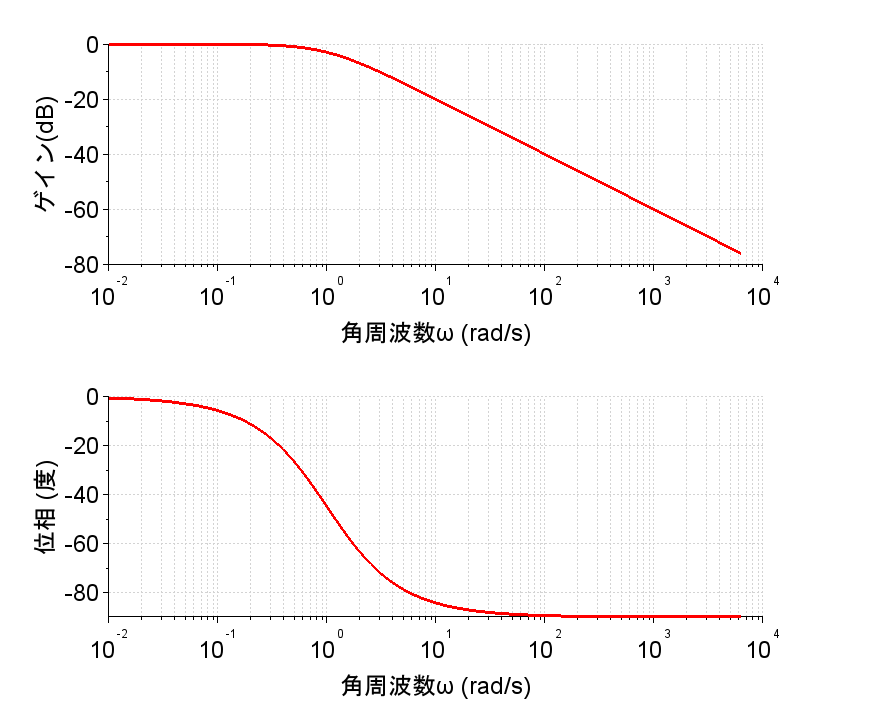
一次遅れ要素の周波数伝達関数は、$$G(j\omega)=\frac{1}{1+j\omega T}$$なのでゲインは、$$g=20\log\left(\frac{1}{\sqrt{1+(\omega T)^2}}\right)$$ $$=-20\log{\sqrt{1+(\omega T)^2}} [dB] $$ また、位相\(\phi\)は、$$\phi=-\tan^{-1}\left(\frac{\omega T}{1}\right)=-\tan^{-1}(\omega T) [\text{°}] $$ となる。
\(\omega T \ll 1\)のとき、\(g \approx 0[dB]\), \(\phi \approx 0\text{°}\)
\(\omega T =1 \)のとき、\(g = -3[dB]\), \(\phi = -45\text{°}\)
\(\omega T \gg 1 \)のとき、\(g \approx -20\log(\omega T) [dB]\)に漸近し, \(\phi \approx -90\text{°}\)に漸近する。
二次遅れ要素のボード線図
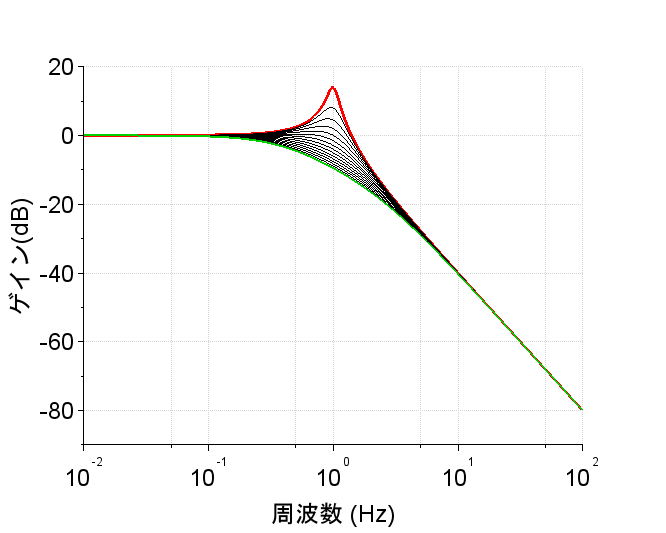
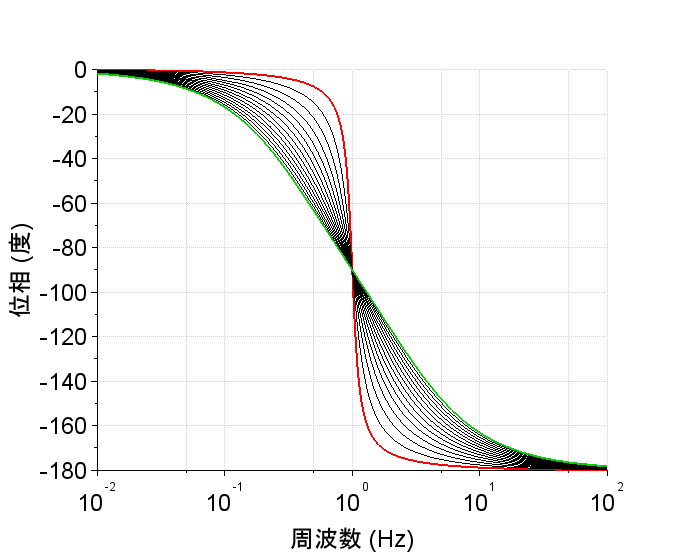
自然周波数\(f_n\)を1[Hz] (自然角周波数\(\omega_n=2\pi f_n\))とし、減衰係数 \(\zeta \) を0.1~1.5まで0.1刻みで変化させて、ゲインー周波数特性、位相ー周波数特性を描いた。横軸が周波数[Hz]であることに注意。緑の線が\(\zeta=1.5\)、赤の線が\(\zeta=0.1\)の場合である。\(\zeta\)が小さいほどゲイン特性では自然周波数\(f_n\)近傍でゲインが増大する、また、位相特性では自然周波数\(f_n\)近傍で大きく位相が変化する。
二次遅れ要素の伝達関数は、$$G(s)=\frac{\omega_n^2}{s^2+2\zeta \omega_n s + \omega_n^2}$$ここで、\(\omega_n\):自然角周波数、\(\zeta\) :減衰係数 である。この周波数伝達関数は、\(s \rightarrow j\omega\)として、$$G(j\omega)=\frac{\omega_n^2}{-\omega^2 + j2 \zeta \omega_n \omega + \omega_n^2}$$ $$ = \frac{1}{1 - \left(\frac{\omega}{\omega_n}\right)^2+j2\zeta \left(\frac{\omega}{\omega_n}\right)} $$
角周波数を\(\Omega=\frac{\omega}{\omega_n}\)で規格化すると、$$G(j\omega)=\frac{1}{1 - \Omega^2+j2\zeta \Omega} $$なので、ゲイン:$$20\log\left|G(j\omega)\right| = 20\log\left(\frac{1}{\sqrt{(1 - \Omega)^2 + 4 \zeta^2 \Omega^2} }\right)$$
$$= -20\log\sqrt{(1-\Omega)^2 + 4 \zeta^2 \Omega^2}$$ 位相:$$\arg G(j\omega)=\tan^{-1}\left(\frac{2 \zeta \Omega}{1 - \Omega^2} \right)$$ となる。これより、
\(\Omega \ll 1\)のとき、\(g \approx 0[dB]\), \(\phi \approx 0\text{°}\)
\(\Omega =1 \)のとき、\(g = -20\log(2\zeta) [dB]\), \(\phi = -90\text{°}\)
\(\Omega \gg 1 \)のとき、\(g \approx -40\log \Omega [dB]\)に漸近し, \(\phi \approx -180\text{°}\)に漸近する。
Scilabによるボード線図の描き方
//一次遅れ系のボード線図
clear; clf();
s=%s;
//時定数 T=1
T=1;
G=1/(T*s+1); /* 一次遅れ要素の伝達関数 */ Gs=syslin('c',G); /* Scilab 内部のシステム表現に変換 */
bode(Gs,'rad'); /* 横軸は角周波数 'rad'オプション */
//2次遅れ系のボード線図
clear; clf();
s=%s;
//自然周波数fn 1[Hz], 自然角周波数wn=2*pi*fn[rad/s]
fn=1;
wn=2*%pi*fn;
//減衰係数 zeta (減衰係数を0.1から0.1刻みで1.5まで変える)
for zeta=0.1:0.1:1.5
G=(wn*wn)/(s^2+2.*zeta*wn*s+wn*wn); /* 伝達関数 */
Gs=syslin('c',G); /* Scilab 内部のシステム表現に変換 */
//ボード線図
scf(0);
gainplot(Gs,0.01,100); /* ゲインー周波数特性 */
scf(1);
phaseplot(Gs,0.01,100); /* 位相ー周波数特性 */
end; /* for - end */
一次遅れ系のボード線図を描くスクリプトでは、bode関数を使用して横軸を角周波数で描いた。なお、bode関数のオプション'rad’を省略すると横軸は周波数[Hz]になる。詳細は、こちらを参照して欲しい。
二次遅れ系のボード線図を描くスクリプトでは、gainplot関数とphaseplot関数を使用している。\(\zeta\)を変化させないボード線図を描くのであれば、bode関数を用いた方が手軽である。


“19. ボード線図” に対して2件のコメントがあります。
コメントは受け付けていません。