9. 伝達関数

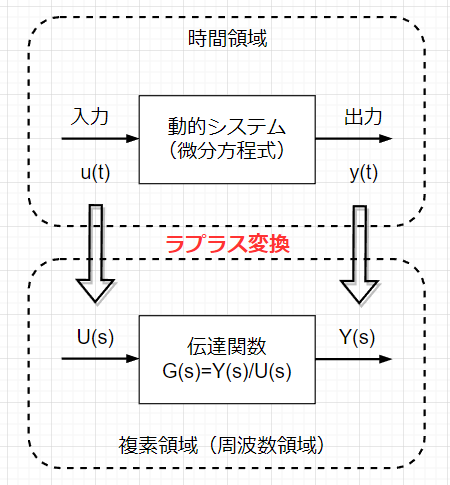
動的システムの入出力関係は、多くの場合微分方程式で記述できる。この微分方程式をラプラス変換し、入出力の比で表現したのが、伝達関数である。
伝達関数の例(RLC回路)
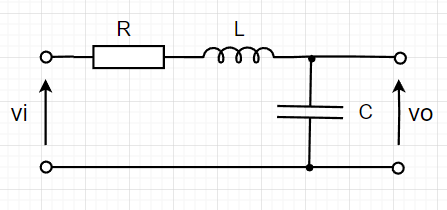
RLC回路の微分方程式は、$$LC\frac{d^2v_o(t)}{dt^2} + RC\frac{dv_o(t)}{dt} + v_o(t) = v_i(t)$$と表せる。\(v_o(0)=0\) , \(\frac{dv_o(t)}{dt}=0\)として、ラプラス変換すると、$$LCs^2 V_o(s)+ RCsV_o(s) + V_o(s) = V_i(s)$$ $$( LCs^2 + RCs + 1)V_o(s) = V_i(s)$$ よって、入力\(V_i(s)\)、出力\(V_o(s)\)として、伝達関数\(G(s)\)は、$$G(s)=\frac{V_o(s)}{V_i(s)}=\frac{1}{LCs^2 + RCs +1} \\ = \frac {\frac{1}{LC}}{s^2+\frac{R}{L}s +\frac{1}{LC}} $$ である。

伝達関数を求めるために、微分方程式をラプラス変換するが、このとき初期値は0と考えて良い。これは、動的システムの初期状態が静的な状態(停止状態や平衡状態)であること、また、伝達関数が、初期値が無視できる定常状態での入出力関係を扱っていることによる。
基本的な伝達関数
(1)比例要素 $$G(s)=\frac{Y(s)}{U(s)}=K$$
(2)積分要素 $$G(s)=\frac{Y(s)}{U(s)}=\frac{1}{T_Is}$$
(3)微分要素 $$G(s)=\frac{Y(s)}{U(s)}=T_D s$$
(4)一次遅れ系 $$G(s)=\frac{Y(s)}{U(s)}=\frac{1}{1+sT}$$ $$\frac{1}{1+sT}=\frac{\frac{1}{T}}{s+\frac{1}{T}}$$ $$\mathcal{L}^{-1}\{G(s)\} = \frac{1}{T}e^{-\frac{1}{T}}$$
(5)二次遅れ系 $$G(s)=\frac{Y(s)}{U(s)}=\frac{K^{'}}{s^2 + as +b}$$ $$G(s)=K\frac{\omega_n^2}{s^2 + 2\zeta \omega_n s + \omega_n^2}$$
伝達関数を求める際の初期値について



“9. 伝達関数” に対して2件のコメントがあります。
コメントは受け付けていません。