29. インピーダンスとアドミタンス
複素インピーダンス
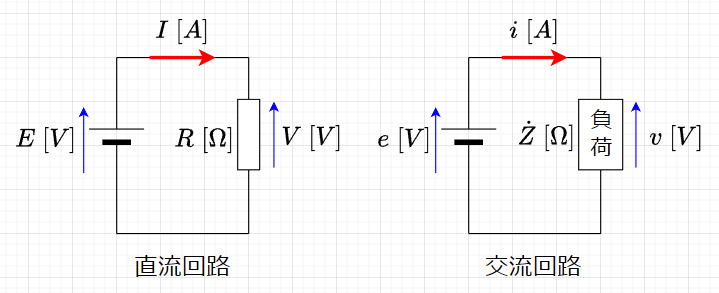
図「直流回路と交流回路」の直流回路では、オームの法則により、電圧\(V\;[V]\)、電流\(I\;[A]\)、抵抗\(R \;[\Omega]\)の間に$$R = \frac{V}{I} \; [\Omega]$$の関係が成立し、抵抗は電流の流れを妨げる。
一方、交流回路では、回路の電流を妨げる働きは負荷で、その素子には抵抗、インダクタ(コイル)、キャパシタ(コンデンサ)がある。
交流回路の図において、交流起電力\(e = E_m \sin \omega t \;[V]\)を負荷に加えると、交流電流\(i \; [A]\)が流れて、負荷の両端に電圧降下\(v \; [V]\)が生じる。この電圧\(v\)は、交流起電力\(e\)に等しく、\(e \;[V] = v \;[V]\)であり、実効値で表すと、\(E\;[V] = V \;[V]\)である。
電圧、電流の実効値\(V \;[V] ,I \;[A]\)とインピーダンス\(Z\;[\Omega]\)との間には、$$Z=\frac{V}{I} \;[\Omega]$$の関係がある。また、複素数の絶対値(大きさ)に交流の実効値を用いて、\(v, \;i\)を複素数表示した\(\dot{V} \;[V], \; \dot{I}\;[A]\)を、$$\dot{V} = Ve^{j\omega t} \; [V] \\ \dot{I} = Ie^{j \omega t} \; [A]$$とする。従って、\(\dot{V}\)と\(\dot{I}\)の間には、$$\frac{\dot{V}}{\dot{I}} = \frac{Ve^{j \omega t}}{Ie^{j (\omega t - \theta)}} = \frac{Ve^{j\omega t - j(\omega t -\theta)}}{I} = \frac{V}{I} e^{j \theta} = Z e^{j \theta}\; \cdots\cdots (1)$$の関係がある。ここで、\(Z=\frac{V}{I}\)である。 式\((1)\)をオイラーの公式を使って直交座標系で表すと、$$\dot{Z} = \frac{\dot{V}}{\dot{I}} = Z e^{j \theta} =Z (\cos \theta + j \sin \theta) = R + j X \; [\Omega]$$となり、複素インピーダンス、または、単にインピーダンスという。実部 \(\mathrm{Re}\{\dot{Z}\}=R = Z \cos \theta\)が抵抗分で、虚部 \(\mathrm{Im}\{\dot{Z}\} =X = Z \sin \theta\)がリアクタンス分である。
また、\(Z\)をインピーダンスの絶対値または大きさといい、\(\theta\)をインピーダンス角または力率角という。\(\dot{Z}\)を用いれば、電圧、電流はそれぞれ、$$\dot{V} = \dot{Z} \dot{I} \;[V] \\ \dot{I} = \frac{\dot{V}}{\dot{Z}} \;[A]$$と表せる。
アドミタンス
並列回路の計算は直列回路に比べると複雑になるが、インピーダンスの逆数を並列回路の計算に用いると直列回路におけるインピーダンスと同様の形式が得られる。インピーダンス\(Z\)の逆数を$$Y = \frac{1}{Z} =\frac{I}{E} \;[S]$$と定め、アドミタンスと呼ぶ。単位は\([S]\)、ジーメンスである。
また、抵抗\(R \; [\Omega]\)の逆数を$$G = \frac{1}{R} \; [S]$$と定め、コンダクタンスと呼ぶ。リアクタンス\(X \;[\Omega]\)の逆数を$$B = \frac{1}{X} \; [S]$$と定め、サセプタンスと呼ぶ。
さらに、誘導性リアクタンス\(X_L = \omega L \;[\Omega]\)、容量性リアクタンス\(X_C = \frac{1}{\omega C} \;[\Omega]\)の逆数をそれぞれ誘導性サセプタンス(\(B_L = \frac{1}{X_L} = \frac{1}{\omega L} \; [S]\))、容量性サセプタンス(\(B_C = \frac{1}{X_C} = \omega C\;[S]\))と呼ぶ。
インピーダンス、アドミタンスの使用例
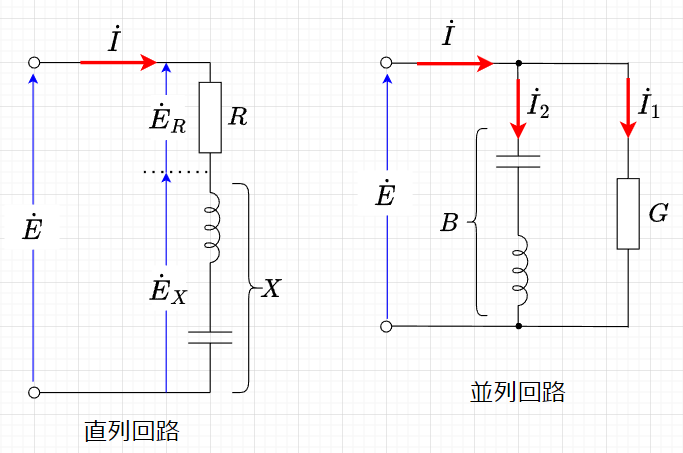

並列回路で、端子電圧を基準にとりアドミタンスで表すと、直列回路で全電流を基準にとりインピーダンスで表した場合と同様の関係になる。
図「直列回路と並列回路」についてのベクトル図を「直列回路、並列回路のベクトル図」に示す。
インピーダンス、アドミタンスの関係を使って、直列回路の\(R,\;X\)と等価な並列回路の\(G,\;B\)を求めることを考える。ベクトル図を参照すると、$$Y = \sqrt{G^2 + B^2} =\frac{1}{Z} = \frac{1}{\sqrt{R^2 + X^2}} \\= \sqrt{\left(\frac{R}{R^2 +X^2} \right)^2 +\left(\frac{X}{R^2 + X^2} \right)^2}$$になるので、$$G = \frac{R}{R^2 + X^2} =\frac{R}{Z^2} \; [S] \;\;\;\;\;\;\;\;\; B = \frac{X}{R^2 + X^2} = \frac{X}{Z^2} \; [S]$$あるいは、$$R = \frac{G}{G^2 + B^2} = \frac{G}{Y^2} \; [\Omega] \;\;\;\;\;\;\;\;\; X = \frac{B}{G^2 + B^2} = \frac{B}{Y^2} \;[\Omega]$$と求まる。
複素インピーダンスによる交流回路の取り扱い
交流の電圧、電流、インピーダンスを複素数で表示して計算すると、効率よく回路解析ができる。ベクトル図における、ベクトルの大きさと位相角を同時に扱えるので、是非、修得して欲しい。(複素数による表示は制御工学の基本的な手法でもある。)
抵抗\(R\)だけの回路
図「抵抗\(R\)だけの回路」において、$$v=V_m \sin \omega t \;[V] \\ i = I_m \sin \omega t \; [A]$$であるが、\(v , \; i\)を複素数表示すると、$$\dot{V} = V_m e^{j \omega t} \; [V] \\ \dot{I} = I_m e^{j \omega t} \; [A]$$となる。
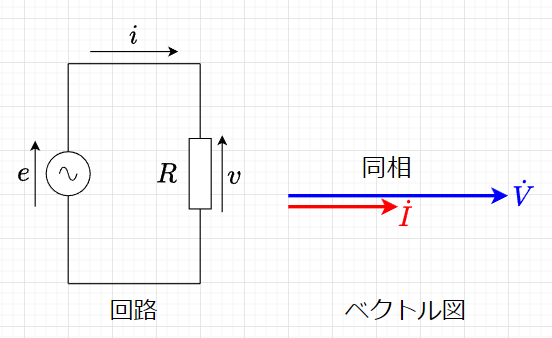
従って、回路のインピーダンス\(\dot{Z} \;[\Omega]\)は、$$\dot{Z} = \frac{\dot{V}}{\dot{I}} = \frac{V_m e^{j \omega t}}{I_m e^{j \omega t}} = \frac{V_m}{I_m} e^{j(\omega t - \omega t)} = R \; [\Omega]$$となる。
キャパシタンス\(C\)だけの回路
図「キャパシタンス\(C\)だけの回路」において、\(v , \; i\)を複素数表示すると、$$\dot{V} = V_m e^{j \omega t} \; [V] \\ \dot{I} = I_m e^{j \omega t + \frac{\pi}{2}} = j \omega C \dot{V} \; [A]$$となる。
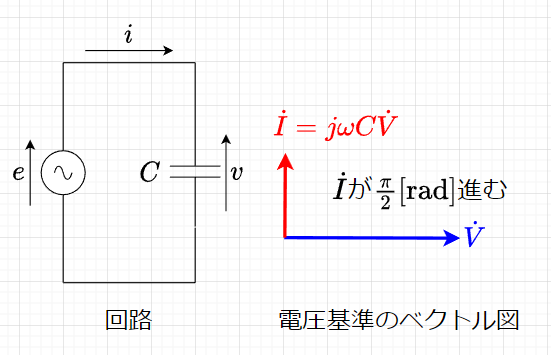
従って、回路のインピーダンス\(\dot{Z} \;[\Omega]\)は、$$\dot{Z} = \frac{\dot{V}}{\dot{I}} = \frac{\dot{V}}{j \omega C \dot{V}} = \frac{1}{j \omega C} = -j \frac{1}{\omega C} = -j X_C\; [\Omega]$$となる。虚部が負であるインピーダンスの虚部\(X_C\)を、容量性リアクタンスという。
インダクタンス\(L\)だけの回路
図「インダクタンス\(L\)だけの回路」において、\(v , \; i\)を複素数表示すると、$$\dot{I} = I_m e^{j \omega t} \; [A] \\ \dot{V} = V_m e^{j \omega t + \frac{\pi}{2}} = j \omega L \dot{I} \; [A]$$となる。
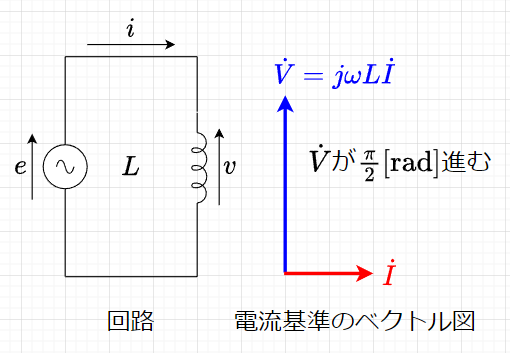
従って、回路のインピーダンス\(\dot{Z} \;[\Omega]\)は、$$\dot{Z} = \frac{\dot{V}}{\dot{I}} = \frac{j \omega L\dot{I}}{\dot{I}} = j \omega L = j X_L\; [\Omega]$$となる。虚部が正であるインピーダンスの虚部\(X_L\)を、誘導性リアクタンスという。
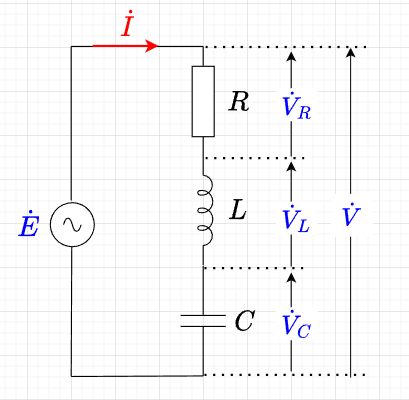
インピーダンスの直列回路
図「\(RLC\)直列回路」において、$$\dot{V} = \dot{V}_R + \dot{V}_L +\dot{V}_C = R \dot{I} + j \omega L \dot{I} - j\frac{1}{\omega C} \dot{I} \\ = R \dot{I} +j \left(\omega L - \frac{1}{\omega C} \right) \dot{I} \; [V]$$となる。
従って、この回路のインピーダンスは、$$\dot{Z} = \frac{\dot{V}}{\dot{I}} = R + j\left(\omega L - \frac{1}{\omega C} \right) \; [\Omega]$$となる。このように、\(RLC\)直列回路のインピーダンス\(\dot{Z}\)は、抵抗とリアクタンスの和の形になる。


“29. インピーダンスとアドミタンス” に対して2件のコメントがあります。
コメントは受け付けていません。