30. 直列共振と並列共振
直列共振回路
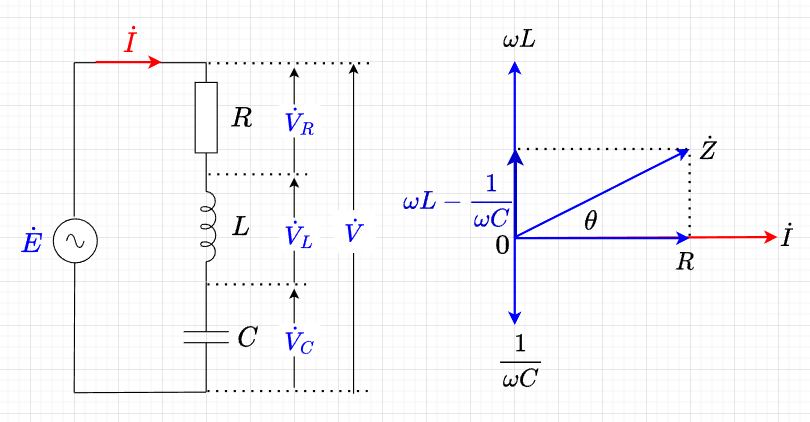
図「直列共振回路」で、電源\(\dot{E}\)の周波数を変化させると、\(X_L = X_C\)、つまり \( \omega L= \frac{1}{\omega C}\)となる周波数が存在する。この周波数のとき、回路のインピーダンスは、$$Z=\sqrt{R^2 + \left(\omega L - \frac{1}{\omega C}\right)^2} \\ = \sqrt{R^2 + 0^2} = R \; [\Omega]$$となる。
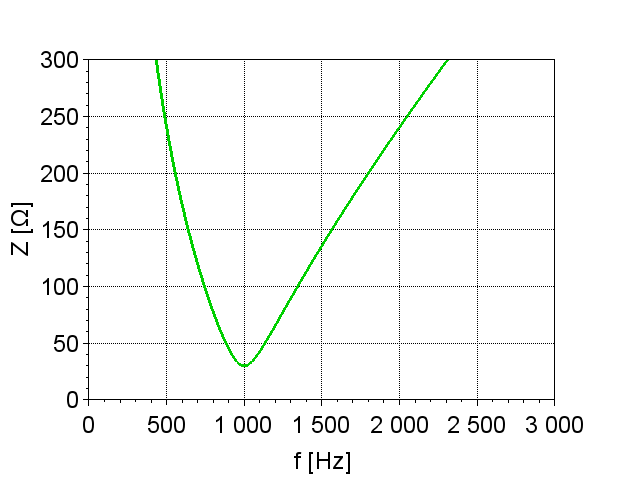
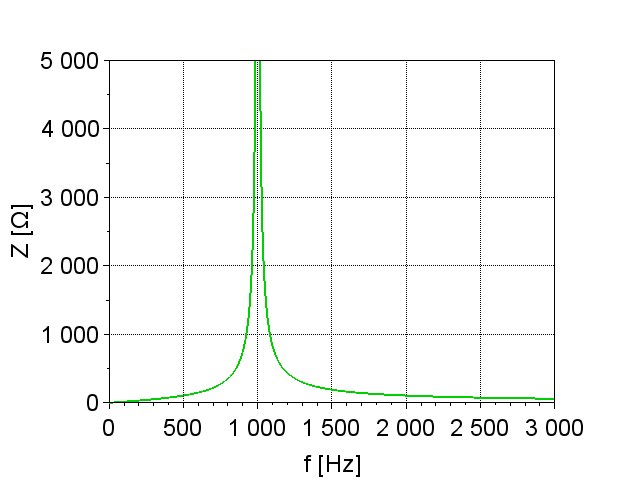
図「インピーダンス\(Z\)の変化は、周波数\(f\)に対するインピーダンス\(Z\)の変化を示したものである。
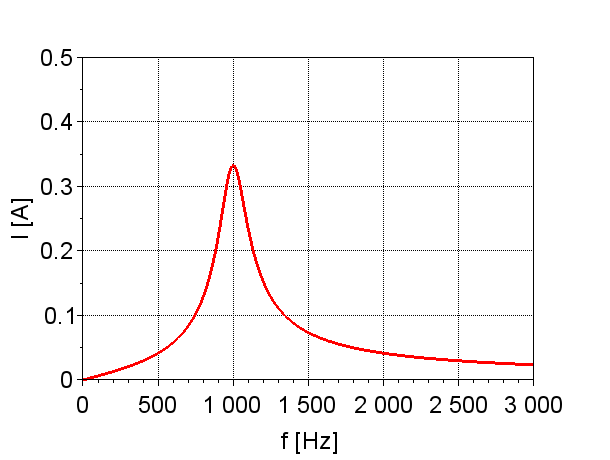
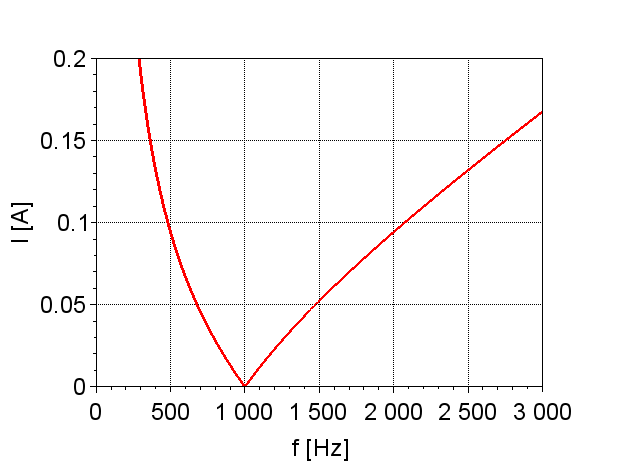
\(Z=R\)となった時の回路電流を共振電流と呼ぶ。共振電流は、$$I_R = \frac{E_m}{R} \; [A]$$である。つまり、共振電流\(I_R\)の大きさは、抵抗\(R\)によって定まり、図「回路電流の変化」に示すように最大となる。このとき、電圧\(V\)と電流\(I\)は同相となる。
この現象を直列共振といい、このときの周波数\(f_r\)を共振周波数という。
共振周波数は、\(\omega L = \frac{1}{\omega C}\)より、$$\omega_ r= \frac{1}{\sqrt{LC}} \; [\mathrm{rad}/s] \;\;\;\;\;\;\; f_r = \frac{1}{2\pi \sqrt{LC}} \; [Hz]$$となる。\(\omega_r\)より低い周波数では、\(X_C\)が支配的(容量性)で、\(\omega_r\)より高い周波数では、\(X_L\)が支配的(誘導性)になる。
また、直列共振時には、\(X_L = X_C\)、すなわち、\(V_L = V_C\)となるから、\(V_L , \; V_C\)のそれぞれと\(V\)との比を\(Q\)とすると、$$Q = \frac{V_L}{V} = \frac{V_C}{V} = \frac{\omega_ r L}{R} = \frac{1}{\omega_r CR} = \frac{1}{R}\sqrt{\frac{L}{C}}$$となる。この\(Q\)を選択度、もしくは共振の鋭さと呼ぶ。
並列共振回路
図「並列共振回路」において、インダクタンス\(L\)に流れる電流を\(I_L\)、キャパシタンス\(C\)に流れる電流を\I_C\)とすれば、$$I_L = \frac{V}{\omega L} \; [A] \\ I_C = \frac{V}{\frac{1}{\omega C}} = \omega C V \;[A]$$となる。
直列共振回路と同様に、ある周波数で\(\omega_r L = \frac{1}{\omega_r C}\)が成り立ち、図「インピーダンス\(Z\)の変化」のように、この共振周波数でインピーダンスが無限大になる。このとき、\(\dot{I}_L\)と\(\dot{I}_C\)は打ち消し合い、電流\(I\)は図「回路電流の変化」のように零となる。
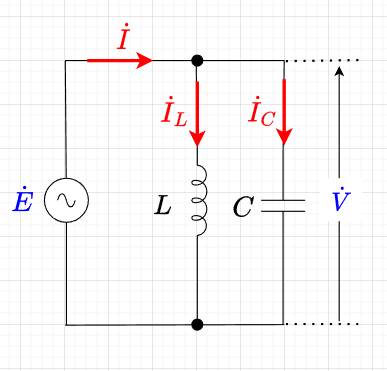
この現象を並列共振、反共振という。
共振周波数\(f_r\)は、$$f_r = \frac{1}{2\pi \sqrt{LC}} \; [Hz]$$で求められる。
実際の回路では、インダクタ(コイル)に含まれる抵抗分によって、インピーダンスは有限の値をとる。
この回路は、高周波の発振回路などに利用される。


“30. 直列共振と並列共振” に対して1件のコメントがあります。
コメントは受け付けていません。