14. 状態観測器

状態観測器は、制御対象の状態を推定する仕組みである。制御対象の状態は、例えば、速度、位置、角度、温度、圧力などの物理量で表される。制御対象の状態を正確に知ることができれば、正確な制御が可能となる。
状態観測器は、制御対象からの出力信号と入力信号を用いて、制御対象の状態（状態変数）を推定する。
状態観測器の構成は、状態フィードバック制御と密接に関連している。状態フィードバック制御は、制御対象の状態変数を直接観測できる場合に適用されるが、制御対象の状態変数が観測できない場合には状態観測器（オブザーバ）を使用する。

状態フィードバックの問題点

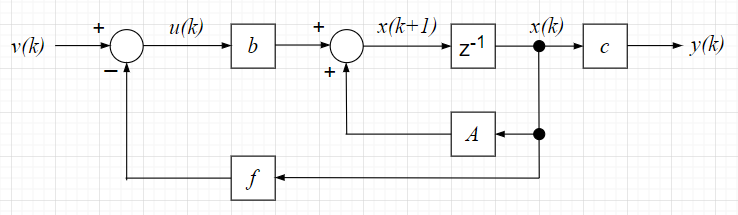
状態フィードバックは全ての状態変数を測定してフィードバックをかけることで、安定化と極配置を実現する。以下の状態方程式、出力方程式、操作量で表せる。$$x(k +1 ) =A x(k) + b u(k) \;\;\; , \;\;\; y(k) = c x(k) \;\;\; , \;\;\; u(k) = -f x(k) +v(k)$$ \(f = \begin{bmatrix} f_1 & f_2 & \cdots & f_n \end{bmatrix}\)：状態フィードバックゲイン　、　\(v(k)\)：外部入力

状態フィードバックは、全ての状態変数を測定できることが前提となっている。そのため、制御器の実装上は困難な場合が多い。　このことから、状態変数の推定が必要となる。この状態推定を状態観測器（オブザーバ）が行う。

※近年では、センサ（特に半導体センサ）の発達で直接測定できる状態変数が多くなっている。例えば、ドローンの飛行姿勢制御には、多軸の加速度センサやジャイロセンサが使われており、高度な飛行制御が可能となっている。

状態観測器（オブザーバ）の基本的な発想

$$x(k +1) = Ax(k) + bu(k) \;\;\; ,\;\;\; y(k) = c x(k) \;\;\;, \;\;\; x(0) = x_0$$のシステムにおいて、測定可能な入力\(u(k)\)と出力\(y(k)\)から状態変数\(x(k)\)を推定するシステムが状態観測器である。

状態変数の推定値を\(\hat{x}(k)\)として、推定誤差を \(e(k) = x(k) - \hat{x}(k)\) とおくと、状態観測器は初期状態 \(x(0)\) に対して　\(\lim_{k \rightarrow \infty} e(k) = 0\) を満たさなければならない。

\(A \;\; , \;\; b\)は既知なので、$$\hat{x}(k+1) = A \hat{x}(k) + b u(k) \;\;\;\ \hat{x}(0) = \hat{x}_0$$
このとき、誤差は、$$ e(k+1) = x(k+1) - \hat{x}(k+1) \\ = A x(k) + b u(k) - \left\{ A \hat{x}(k) + b u(k)\right\} = A \left\{x(k) - \hat{x}(k)\right\} = Ae(k)$$となる。\(e(0) = e_0\)として、システム行列\(A\)が安定なら$$\lim_{k \rightarrow \infty} e(k) = \lim_{k \rightarrow \infty} A^k e_0 = 0$$となる。このようにシステム行列\(A\)が安定であれば、\(\hat{x}(k)\)は容易に求まる。しかし、このままでは、\(A\)が不安定なら誤差\(e(k)\)は発散してしまう。この問題を解決したのが状態観測器の構造である。

状態観測器（オブザーバ）の構造

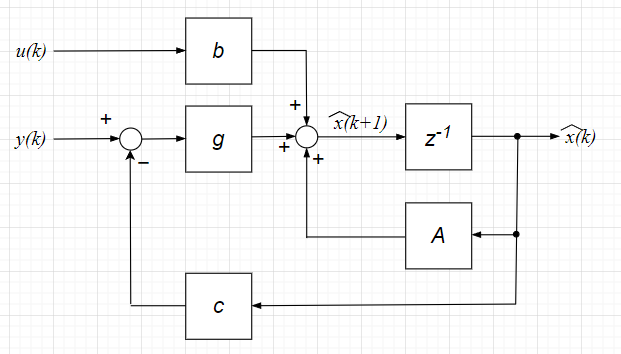
状態変数の推定値から出力の推定値を算出し、出力の推定誤差に基づいて修正項を追加する構造を考える。式で表すと$$\hat{x}(k+1) = A \hat{x}(k) + b u(k) + g \left( y(k) - \hat{y}(k) \right) \;\;\; , \;\;\; \hat{y}(k) = c \hat{x}(k)$$ 　となる。\(g = \begin{bmatrix} g_1 & g_2 & \cdots & g_n \end{bmatrix}\)：観測器ゲイン　。これにより、誤差\(e(k)\)は　$$e(k+1) = x(k+1) - \hat{x}(k+1) \\ = Ax(k) + b u(k) - \left\{A \hat{x}(k) + b u(k) + g\left( c x(k) - c \hat{x}(k)\right) \right\} \\ = A\left(x(k) - \hat{x}(x)\right) - gc\left(x(k) - \hat{x}(x)\right) \\ = (A - gc)\left(x(k) - \hat{x}(k)\right) = (A -gc)e(k)$$となる。
\(e(k) = (A -gc)e(k)\)なので、\( (A - gc)\)が安定であれば、\(e_0\)に対して、すなわち任意の\(x_0\)に対して、\(e(k) \rightarrow 0\)とできる。この場合、\(A\)は不安定でも良いことになる。

状態観測器（オブザーバ）の極配置

状態観測器での状態変数\(x(k)\)の推定誤差は、$$e(k +1 ) =(A - gc)e(k)$$ となる。制御対象のシステムが可観測であれば、可観測正準形に変換できる。従って、$$A - gc = \begin{bmatrix} 0 & \cdots & 0 & -a_n - g_1 \\ 1 & & & -a_{n-1} -g_2 \\ & \ddots & & \vdots \\ & & 1 & -a_1 - g_n \end{bmatrix}$$ となる。よって、誤差に関する特性方程式は、$$\phi (z) = \left| zI - (A-gc) \right| \\ =z^n +(a_1+g_n)z^{n-1} + \cdots + a_n + g_1$$ となる。
誤差の特性方程式\(\phi(z)\)から、オブザーバゲイン\(g\)を適当に選べば、\((A - gc)\)の固有値を任意に配置できることがわかる。

具体的には、指定したい極を\(\lambda_1 , \lambda_2, \cdots ,\lambda_n\)とすると特性方程式は、$$\phi(z) = (z - \lambda_1)(z - \lambda_2)\cdots (z - \lambda_n) = z^n + \alpha_1 z^{n-1} + \cdots + \alpha_n = 0$$となる。従って、前式の誤差の特性方程式と係数比較すると、\( a_1 + g_n = \alpha_1 , \cdots , a_n + g_1 = \alpha_n\)なので、指定した極を実現するオブザーバゲインは、$$g_i = \alpha_{n-i+1} - a_{n-i+1} \;\;\;\; (i = 1,2,\cdots, n)$$となる。
以上により、任意の極配置を実現するオブザーバーゲインが決定できるので、
\((c , A)\)が可観測であれば、状態観測器の極は任意に配置できる、ことになる。

なお、当然のことながら、オブザーバの極はフィードバックシステム全体の極より、状態変数の推定誤差が速く\(0\)に収束するような極を指定しなければならない。