7. 平均、分散、標準偏差、確率分布
ノイズとS/N比
ノイズ(雑音)とは処理対象となる情報以外の不要な情報のことであるが、測定では主に信号に付随して現れるランダムな電気的波形のことを指します。ノイズは、通信や音響などの多くの分野で問題となるが、測定においては、信号とノイズが混在すると信号を正確に抽出することが難しくなる。
S/N比(Signal-to-Noise Ratio)は、信号の強さとノイズの強さの比率を表す。S/N比が高いほど、信号がノイズに埋もれず明確に観測できるようになる。S/N比が低い場合、信号を正確に認識することが難しくなり、情報の損失やエラーが発生することになる。測定においてS/N比を高くすることが重要になる。
*測定値はノイズなどによりばらつきがある。測定対象となる信号以外の信号はノイズと考える。ノイズ除去にはフィルタなどを使用する。S/N比は以下のように表す。
$$S/N比= \frac{信号のパワー}{ノイズのパワー}$$また、S/N比はdB(デシベル)で表すことが多い。$$S/N比[dB] = 10\log \frac{信号のパワー}{ノイズのパワー} \\ =10\log \frac{信号の電圧の2乗}{ノイズの電圧の2乗} \\ = 20\log \frac{信号の電圧}{ノイズの電圧}$$
※\(\log\)は常用対数である。
パワー (electric power)
パワーは、電圧や電流の2乗に比例する。$$P=VI=I^2R=\frac{V^2}{R}$$
$$S/N比=\frac{信号の電圧の2乗}{ノイズの電圧の2乗}$$
測定値の処理方法
*測定値に誤差が含まれているとき、データを処理して誤差の影響を軽減する。
※ここでは、偶然誤差に対するデータ処理について考える。
偶然誤差とは、測定誤差のうち、ランダムな要因によって生じる誤差のことを指す。このような誤差は、測定器具や測定方法の限界によるものではなく、単に測定時に発生した偶然の要因によって生じるものである。
ガウスの誤差法則(偶然誤差についての法則)
① 小さい誤差は大きい誤差より生じやすい
② 同じ誤差は正負ともに同じ割合で生じる
③ 非常に大きい誤差はほとんど生じない
平均値(標本平均)
測定値のサンプル(標本)を\(x_1,x_2,\cdots,x_n\)とすると、平均値\(\bar{x}\)は、$$\bar{x} = \frac{1}{n} \left(x_1 + x_2 + \cdots + x_n \right) = \frac{1}{n} \sum_{i=1}^{n} x_i$$ ・サンプルデータ数\(n\)が多くなると、平均値に含まれる誤差は小さくなる。
・サンプルを移動しながら平均をとる方法に移動平均法がある。時系列データの雑音を軽減し、変動の傾向を知る方法。定常性、サンプル数、周期などに注意が必要である。(例:新型コロナ感染者数の推移)
平均値(母平均)
母平均、標本平均
・母平均は「母集団全体」の平均
・標本平均は「母集団から抽出した一部」の平均
標本平均 \(\bar{x}\) において \(n \rightarrow N\)とすると、\(\bar{x} \rightarrow \mu \)となる。
母集団とは、分析の対象となる全ての要素の集合を指す。例えば、ある製品の製造数の全数などが母集団にあたる。
標本とは、母集団の一部をランダムに選択した、代表的な部分集合のことを指す。標本は、母集団全体を検査することが困難な場合に、その一部を検査することで母集団全体についての情報を得ることができる。例えば、ある製品の製造全数を検査することは困難であるが、ランダムに選んだ100個の製品を検査することで、その製品の全数についての状態を推定することができる。
標本を用いた統計的分析や推定は、母集団全体を検査するよりもコストが低く、時間が短く済む。しかし、標本を選ぶ方法や標本の大きさなどによって、推定結果に偏りが生じる可能性がある。
測定値の母集団を\(x_1,x_2,\cdots,x_N\)とすると、母集団の平均値\(\mu\)は、$$\mu = \frac{1}{N}\left(x_1 + x_2 + \cdots + x_N \right) = \frac{1}{N} \sum_{i=1}^{N} x_i \;\;\;\; (N \gg n)$$
標本分散\(\sigma^2\)、標準偏差\(\sigma\)
標本分散\(\sigma^2\) とは、データの散らばり具合を表す指標の1つで、標本の各データとその平均値との偏差を2乗し、それらの平均値を求めたものである。また、標本標準偏差\(\sigma\) は、標本分散の正の平方根であり、標本のデータの散らばり具合を表す指標の1つである。$$\sigma^2 = \frac{1}{n}\sum_{i=1}^{n} \left(x_i - \bar{x}\right)^2$$ $$\sigma = \sqrt{\frac{1}{n}\sum_{i=1}^{n} \left(x_i - \bar{x}\right)^2 }$$
偏差 (deviation)
測定値と平均値の差を偏差(deviation)という。
不偏分散\(s^2\) 、不偏標準偏差\(s\)
不偏分散とは、母集団から取得した標本における分散を推定するために用いられる指標であり、標本分散の修正版である。標本分散では標本平均を用いるため、標本の分散が母集団の分散を過小に評価する場合があるが、不偏分散では標本の自由度を考慮することで、母集団の分散をより正確に推定することができる。しかし、標本の分散値が母集団の分散値と一致するわけではないため、不偏分散も母集団の分散値と完全に一致するとは限らない。また、不偏分散は計算がやや複雑であるため、標本が大きい場合は標本分散でも十分な場合がある。$$s^2 = \frac{1}{n-1}\sum_{i=1}^{n} \left(x_i - \bar{x}\right)^2$$ $$s = \sqrt{\frac{1}{n-1}\sum_{i=1}^{n} \left(x_i - \bar{x}\right)^2 }$$
ガウス分布(正規分布)
ガウス分布とは、連続型の確率分布の一種で、正規分布とも呼ばれる。一般的には、連続的な実数値のデータが平均値を中心に正規分布に従うことが多く、多くの統計学的手法や自然科学の現象において、ガウス分布は広く使われている。
ガウス分布の確率密度関数 \(f(x)\)は、$$f(x) = \frac{1}{\sqrt{2 \pi \sigma^2}} \exp \left\{- \frac{(x - \mu)^2}{2 \sigma^2} \right\}$$ である。\(\mu\)は平均値、\(\sigma\)は標準偏差を表す。この式からわかるように、ガウス分布は平均値を中心に左右対称の釣鐘型の形状をしており、標準偏差が小さくなるほどピークが高く、標準偏差が大きくなるほどピークが低く広がっていく。
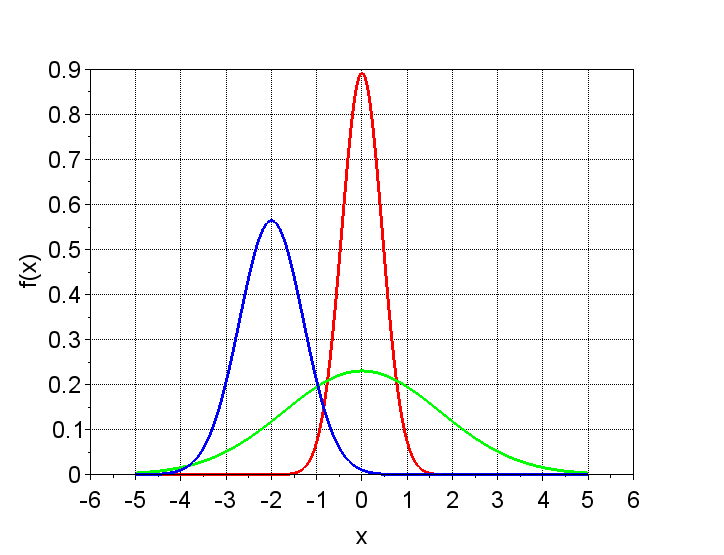
赤線:\(\mu = 0 \;\;\; \sigma^2 = 0.2\)
緑線:\(\mu = 0 \;\;\; \sigma^2 = 3.0\)
青線:\(\mu = -2.0 \;\;\; \sigma^2 = 0.5\)
ガウス分布の性質
・確率密度関数\(f(x)\)とは、連続型の確率変数に対してその値がある範囲に含まれる確率を表す。従って、確率密度関数は非負の値をとり、全範囲で積分した値は1になる。$$f(x) \gt 0 \;\;\; , \;\;\;\int_{-\infty}^{\infty} f(x) dx =1$$・\(x = \mu\) つまり平均値を中心に左右対称となる。
・\(x = \mu \pm \sigma\) が変曲点となる。
標準正規分布
ガウス分布の確率密度関数\(f(x)\)で、\(\mu = 0 \;\;, \;\; \sigma^2 = 1\)とすると、$$f(x) = \frac{1}{\sqrt{2\pi}}\exp\left(-\frac{x^2}{2}\right)$$となる。 これを標準正規分布という。
標準正規分布の全確率は、$$\int_{-\infty}^{\infty} f(x)dx=1$$である。また、標準正規分布の期待値(平均)は、$$\int_{-\infty}^{\infty} xf(x) dx = 0$$である。
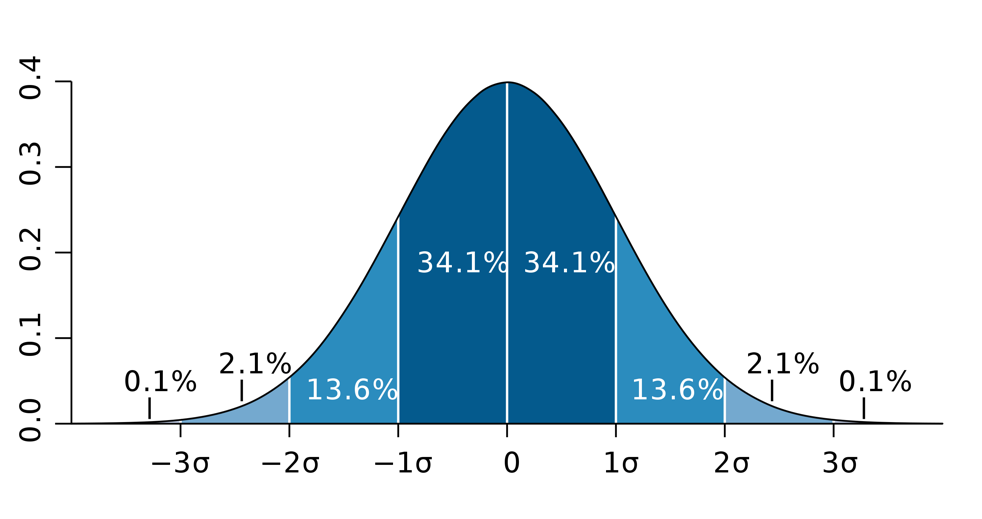
標準正規分布で平均値\(\mu\) からのずれが \(\pm 1 \sigma\) 以下の範囲に\(x\)が含まれる確率は \(68.27\%\)、\(\pm 2\sigma\)以下だと\(95.45\%\)、\(\pm 3\sigma\)以下だと\(99.73\%\)となる。
また、変曲点は\(1\sigma\)(標準偏差 \(\sigma\))となる。
参考
*標準正規分布の全確率
ガウス積分の公式を使って、以下のように計算できる。
$$\int_{-\infty}^{\infty} f(x)dx = \int_{-\infty}^{\infty} \frac{1}{\sqrt{2\pi}}\exp\left(-\frac{x^2}{2}\right)dx \\=\frac{1}{\sqrt{2\pi}} \int_{-\infty}^{\infty} e^{-\frac{x^2}{2}}dx \\=\frac{1}{\sqrt{2\pi}}\sqrt{2} \int_{-\infty}^{\infty} e^{-t^2}dt \\= 1 \;\;\;\;\; \left( \frac{x}{\sqrt{2}} =t と置換\right)$$
*標準正規分布の期待値(平均)
$$ \frac{d}{dt} e^{-\frac{x^2}{2}} = -x e^{-\frac{x^2}{2}}$$の関係を使って以下のように計算できる。
$$\int_{- \infty}^{\infty} xf(x)dx = \frac{1}{\sqrt{2 \pi}} \int_{- \infty}^{\infty} x e^{- \frac{x^2}{2}}dx \\ =- \frac{1}{\sqrt{2\pi}} \left[e^{- \frac{x^2}{2}}\right]_{-\infty}^{\infty} = 0$$
ガウス積分の公式
$$\int_{-\infty}^{\infty} e^{-x^2}dx = \sqrt{\pi}$$
ガウス積分の証明【あえて2乗する驚き】を参考にどうぞ。

