6. 測定値の統計的扱い
測定の正確さ
測定における正確度(確度)(Accuracy)は、測定値が基準値(真値)にどれだけ近いかを示し、つまり正確性を評価する尺度である。例えば、複数回同じ方法で測定を行い、測定値の平均値を求めることで、真の値に近い測定値を得ることができた場合、測定値のばらつきが小さく、測定器や方法の正確度が高いと言える。
測定における精度(precision)は、同じ条件下で測定を繰り返した場合に、測定値がどれだけ近いかを示す指標であり、つまり再現性を評価する尺度である。測定器や方法の精度が高い場合、同じ条件下で測定を繰り返した場合でも、測定値のばらつきが小さく、測定結果が再現性が高いと言える。
従って、測定における正確度は測定値の正確性を評価し、精度は測定結果の再現性を評価する尺度である。両者ともに測定器や方法の性能評価において重要な尺度であり、適切な評価が求められる。
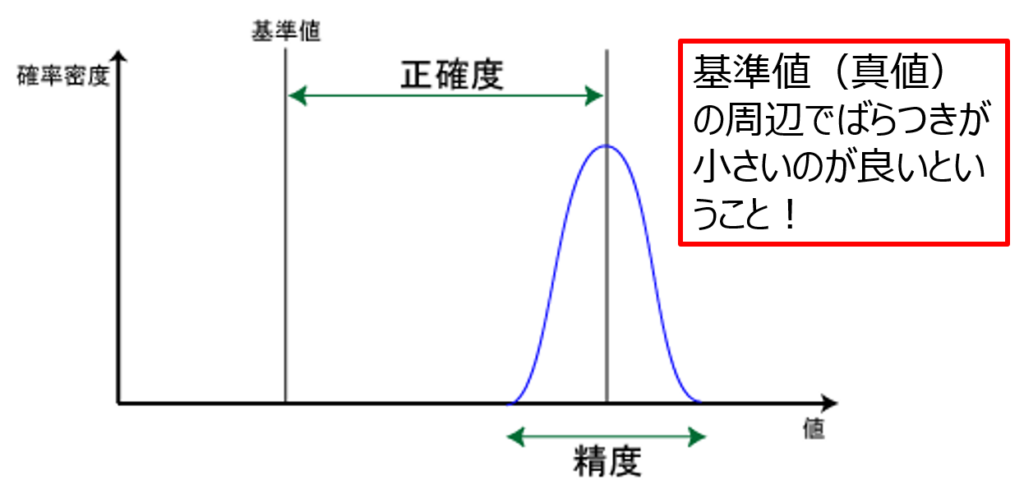
正確度(確度)と精度
正確度(確度)は正確性の尺度であり、精度は再現性の尺度である。
※確率密度:確率密度は定義域内での値の「相対的な出やすさ」を表すもの。
出典:https://www.hitachi-hightech.com/jp/ja/knowledge/semiconductor/room/manufacturing/accuracy-precision.html
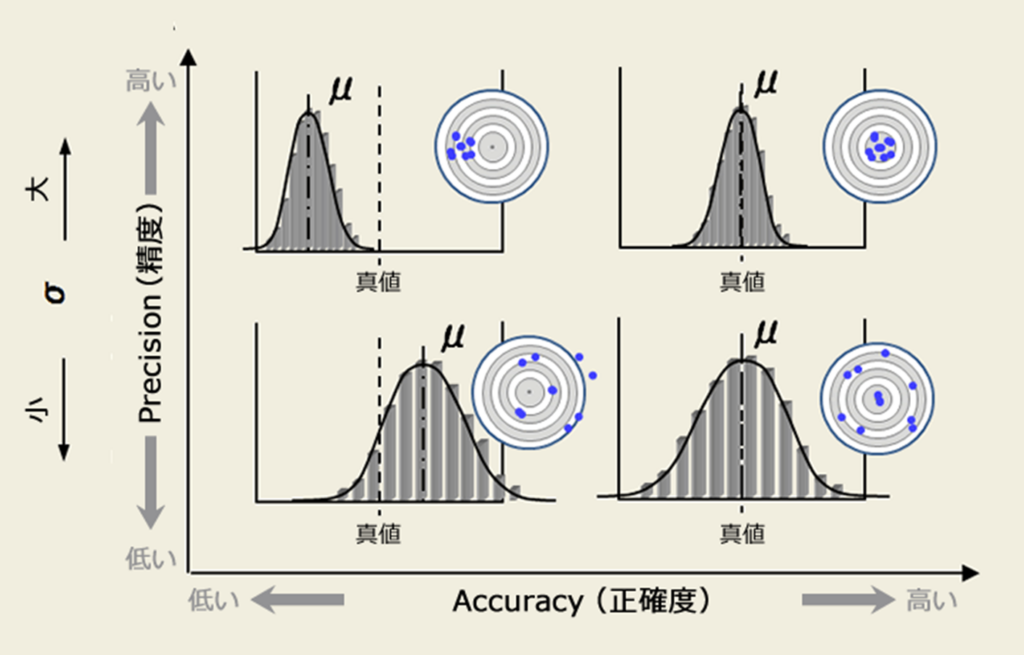
計測値を度数分布で表したものが、図「正確度と精度」で、多くの計測データを収集すると、データの分布は、ガウス(正規)分布に近づく。分布の特徴は、平均値:μと標準偏差:σで表される。
正確度と精度の両方が高いと的の図からわかるように、測定点が中心に集まる。正確度と精度の両方が低いと、測定点が中心からずれ偏りがあり、バラツキが大きい。
有効数字、有効桁数
*測定値や測定値を使った計算で得られた値は、末位に誤差を含みながら、測定値として意味をもつ桁だけを表示したものが有効数字である。
【例】最小目盛りが1mmの定規
この定規で長さをはかったとき、端が12mmと13mmのちょうど真ん中にかかったとする。 このとき長さを12mmまたは13mmとするより12.5mmとする方が実際の長さに近くなる。この測定結果「12.5mm」は、末位の「5」に誤差を含みながらも測定値として有効な桁だけを表示した有効数字といえる。
有効数字の桁数の数え方
1.0 有効数字2桁
1.01 有効数字3桁
0.10 有効数字2桁 (末位の「0」も数える)
0.010 有効数字2桁
大きい有効数字、または小さい有効数字は、一桁目と二桁目の間に小数点がくるよう指数で調整して表示する。
0.0000110 \(\rightarrow\) \(1.10×10^{-5}\) 有効数字3桁
11000000 \(\rightarrow\) \(1.10×10^7\) 有効数字3桁
*有効数字の計算
誤差が拡大したり不要な桁が増えたりしないように切り捨てを行いながら計算を進め、最終的な答えを出すときに四捨五入を行う。
【例】有効数字3桁で答えるよう指定されているとする。次の規則で計算を進める。
①途中計算は求める答えより1桁多い4桁を残し,以下を切り捨て
②最終的な答えだけ残しておいた4桁目を四捨五入して3桁とする
この規則に従って計算すると、
34.97×0.7577=26.4967…4桁を残し,以下を切り捨て
36.97×0.2423= 8.95783…4桁を残し,以下を切り捨て
26.49+8.957=35.447
残しておいた4桁目を四捨五入して有効数字3桁にする
35.44 \(\rightarrow\) 35.4 \(\cdots\)有効数字3桁の答え
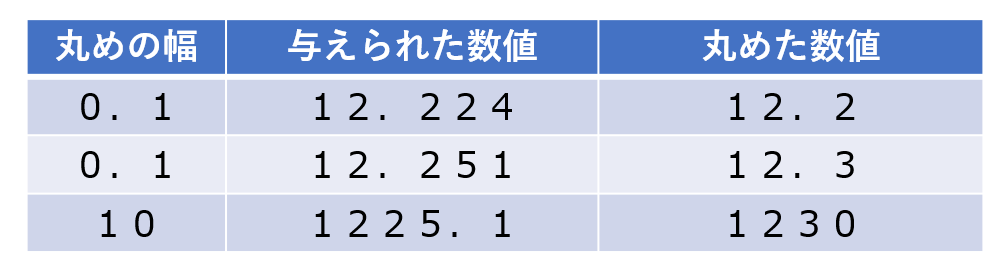
【例】数値 2.35 は 2.345 を四捨五入したものであることがわかっているとする。有効数字2桁に丸めるといくらになるか
答:2.3(有効数字2桁にするのだから3桁目を四捨五入する)
\(2.345 \rightarrow 2.35(3桁)\rightarrow 2.4(2桁)\)としてはいけない!
※多数桁の測定値が複数あるデータを整理する時についやってしまいがち。
四捨五入と切り捨てによる誤差
*「数値の丸め」:数値をある規則で置き換えること ⇒ 一般に四捨五入が使われる。(負の数では絶対値に対して適用する。)
*丸めはつねに1回とする → 2回以上は誤差拡大の原因となる【例】 7.346 を2桁に丸めると 7.3 であるが、2段階で丸めると
\(7.346 \rightarrow 7.35 \rightarrow 7.4\)となり、望ましくない。
誤差の伝搬
誤差の伝搬が起こる原因
測定結果を得るのに、測量や計測を行うが測定値をそのまま使うことはまれで、測定値から計算処理することによって測定結果を導く。また測量、計測には計測器の精度や計測器の設定や調整において、様々な誤差が含まれる。
従って、たくさんの測定値を用いる場合には、測定値がどの程度の精度なのか把握しておく必要がある。
測定値の取り扱い、特に測定結果を得る計算処理の過程で誤差の伝搬が起こる。測定値を計算処理する際には、計測器の限界や精度、環境条件の影響、計算処理における数値表現の誤差や近似誤差などが原因として誤差の伝搬を引き起こす。
具体的には、以下のような原因にまとめられる。
・計測器の限界や精度: 計測器には、読み取り誤差や精度の限界などの誤差がある。例えば、測定器の目盛りが1mmの場合でも、目盛りの間に微小な間隔があるため、測定値は必ずしも正確ではない。このような測定器の誤差が、測定値に含まれ、計算処理を行うことで誤差が伝搬していく。
・環境条件の影響: 測定を行う場所や時間によって、測定値に影響を与える環境条件が異なる。例えば、温度や湿度、気圧などの変化は、測定値に誤差を引き起こす可能性がある。また、測定対象の変形や振動、磁場の影響なども測定値に影響を与えることがある。これらの環境条件の影響が、測定値に含まれ、計算処理を行うことで誤差が伝搬する。
・計算処理の誤差: 測定値から測定結果を導く際には、測定値を基に計算処理を行うことが必要である。しかし、計算処理においても、数値表現の誤差や近似誤差などが生じ、誤差の伝搬が起こる。
これらの原因が複合して誤差の伝搬が起こる。測定値から得られた測定結果の精度を向上させるためには、測定器の選定や校正、測定環境の管理、計算処理の適切な手法の選択などが必要である。
誤差の伝搬法則
\(z = f(x,y)\)という関係があるとする。すなわち、\(z\)という測定結果が、測定値\(x,y\)から演算\(f(x,y)\)により求まるとする。
各測定値は誤差を含んでいるので、\(x_0, \;\; y_0\)を真値、\(e_x, \;\; e_y\)を誤差として、$$x = x_0 + e_x \;\;\;\; , \;\;\; y = y_0 +e_y$$と表せる。このとき、\(z_0\)を測定結果から推測される真値として$$z = z_0 \pm e_z \;\;\; , \;\;\; z_0 = f(x_0 , y_0)$$となる。演算\(f\)により伝搬した誤差は、$$e_z = \sqrt{ \left(\frac{\partial f}{\partial x} \right)^2 e_x ^2 + \left(\frac{\partial f}{\partial y} \right)^2 e_y ^2 } $$と表せる。これを誤差の伝搬法則という。
※精密計測を考える場合、いわゆる真値は測定値から推測される真の値ということに注意が必要である。
誤差の伝搬法則の導出
測定値を\(x = x_0 + \Delta x\) 、\(y = y_0 + \Delta y\)のとき、測定結果は \(z = f(x_0 + \Delta x , y_0 + \Delta y) \)と表せる。真の値 \(z = f(x_0 , y_0)\)との誤差は、テイラー展開できることを仮定し、テイラー展開の二次以降の項を無視すると(一次の項で近似するということ)$$\Delta z \simeq \frac{\partial f}{\partial x} \Delta x + \frac{\partial f}{\partial y} \Delta y$$ よって、誤差の二乗の期待値を計算すると$$e_z^2 = E\left[(\Delta z)^2\right] \simeq E\left[\left (\frac{\partial f}{\partial x} \Delta x + \frac{\partial f}{\partial y} \Delta y \right) ^2 \right]$$ $$=E\left[\left(\frac{\partial f}{\partial x}\right)^2 (\Delta x)^2 + \left(\frac{\partial f}{\partial y}\right)^2 (\Delta y)^2 \right]$$ $$=\left(\frac{\partial f}{\partial x}\right)^2 e_x^2 + \left(\frac{\partial f}{\partial y}\right)^2 e_y^2$$ ただし、\(E[\Delta x \Delta y] = 0\) であること(測定誤差\(\Delta x\)と\(\Delta y\)は無相関)を仮定している。
テイラー展開
テイラー展開とは、任意の関数をある一点での導関数の値から計算される項の無限和として関数を表すこと。
分かりやすい解説は、テイラー展開の気持ち【解析学】を参考にしてください。
誤差の伝搬法則の適用例
問題:横の長さの測定値が \(x = (10.0 \pm 0.3)\; cm\) で、縦の長さの測定値が \(y = (5.0 \pm 0.2) \;cm\)の長方形の面積を誤差も含めて求める。
解答:長方形の面積は \(z = (50.0 \pm e_z)\; cm^2 \) である。
誤差\(e_z\)は誤差の伝搬法則の式を使って、以下のように計算できる。
\(z = xy\)より、\(\frac{\partial z}{\partial x} = y \;\; , \;\; \frac{\partial z}{\partial y} = x\) なので、\(\frac{\partial z}{\partial x} = y_0 \;\; , \;\; \frac{\partial z}{\partial y} = x_0\) よって、$$e_z = \sqrt{ \left(\frac{\partial f}{\partial x} \right)^2 e_x ^2 + \left(\frac{\partial f}{\partial y} \right)^2 e_y ^2 } =\sqrt{ y_0^2 e_x ^2 + x_0^2 e_y ^2 } $$ $$= \sqrt{ 5.0^2 \cdot 0.3^2 + 10.0^2 \cdot 0.2^2} = 2.5\;cm^2$$となる。
誤差を含む測定値からの測定結果の計算
二つの測定値の真値を\(x_1 , x_2\)とし、計算結果(測定結果)を\(y\)とする。また、それらに含まれる誤差を\(\Delta x_1 , \Delta x_2 , \Delta y\)とする。
(1)和と差(\(y = x_1 \pm x_2\))
\(y + \Delta y = (x_1 + \Delta x_1) \pm (x_2 + \Delta x_2) = (x_1 \pm x_2) + (\Delta x_1 \pm \Delta x_2)\)
誤差の最大値の見積りは、\(|\Delta y| \le |\Delta x_1| + |\Delta x_2|\)となるが、実際には、\(x_1 , x_2\)が独立であるとき同時に最大になる確率は小さいので、\(|\Delta y| = \sqrt{(\Delta x_1)^2 + (\Delta x_2)^2}\)
※和の誤差を小さくするには、二つの測定値の誤差を同程度に小さくしなければならない。
(2)積(\(y = x_1 x_2\))
\(y +\Delta y = (x_1 + \Delta x_1)(x_2 +\Delta x_2) = x_1 x_2\left( 1+ \frac{\Delta x_1}{x_1} +\frac{\Delta x_2}{x_2} + \frac{\Delta x_1 \Delta x_2}{x_1 x_2} \right) \) 第4項は小さいので無視すると誤差率は、\(\left| \frac{\Delta y}{y} \right| \le \left| \frac{\Delta x_1}{x_1} \right| + \left| \frac{\Delta x_2}{x_2} \right| \)
※積の計算結果の誤差率は、各測定値の誤差率が同程度のときが効率的な測定となる。
(3)商(\(y = x_1 / x_2\))
\( y +\Delta y = \frac{x_1 + \Delta x_1}{x_2 + \Delta x_2} =\frac{x_1}{x_2} \left(\frac{1 + \Delta x_1 / x_1}{1 + \Delta x_2 /x_2} \right) \simeq \frac{x_1}{x_2} \left( 1 + \frac{\Delta x_1}{x_1} - \frac{\Delta x_2}{x_2}\right)\)
\(\left| \frac{\Delta y}{y} \right| \le \left| \frac{\Delta x_1}{x_1} \right| + \left| \frac{\Delta x_2}{x_2} \right| \)
※\(x_1\)と\(x_2\)の誤差率を同程度にすることが、効率的な測定となる。
(4)べき乗(\(y = x_1 x_2^n\))
\(y + \Delta y = (x_1 + \Delta x_1)(x_2 +\Delta x_2)^n \\ = (x_1 + x_2)\left\{ x_2^n +n \Delta x_2 x_2^{n-1} +\frac{n(n-1)}{2!}(\Delta x_2)^2 x_2^{n-2} + \cdots \right\} \\ \simeq x_1 x_2^n \left(1 + \frac{\Delta x_1}{x_1} + n \frac{\Delta x_2}{x_2} \right)\)
\(\left| \frac{\Delta y}{y} \right| \le \left| \frac{\Delta x_1}{x_1} \right| + n \left| \frac{\Delta x_2}{x_2} \right| \)
※\(x_1\)と\(x_2\)の誤差率を同程度にするには、べき乗の項は誤差率を\(1/n\)にしなければならない。
誤差を含む測定値からの測定結果の計算例
【例1】\(100 \; \Omega\)と\(10 \; \Omega\)の抵抗素子がそれぞれ25%の誤差を含む。二つの抵抗素子を直列に接続したときの、抵抗値\(R\)の誤差\(\Delta R\)を求めよ。
解答:
\(R+ \Delta R=100(1 + 0.25) + 10 (1 + 0.25) = 110+25+2.5\)
\(\Delta R = 27.5 \; \Omega\) ※誤差の最大値の見積もり
\(\Delta R = \sqrt{25^2 +2.5^2 } = 25.12 \; \Omega\) ※誤差の見積もり値
【例2】電流\(I = 10 \; mA\)、電圧\(V = 3 \; V\) に誤差が10%含まれる。\( R=V/I\) で抵抗値を求めるとき、誤差\(\Delta R\)、誤差率\(\Delta R /R \)を求めよ。
解答:
\(\Delta R = R \left( \frac{\Delta I}{I} + \frac{\Delta V}{V} \right) = \frac{3}{0.01} (0.1 + 0.1) = 60 \; \Omega \)
\(\frac{\Delta R}{R} = \frac{60}{300} = 0.2\) (20%)

