13. デッドビート制御
デッドビート制御とは有限時間整定制御とも呼ばれ、出力と目標値の偏差を有限ステップ内で零に整定させるディジタル制御手法である。デッドビート制御では、応答が目標値に到達するまでの過渡現象を完全に抑制させることを目指し、定常状態に到達するまでの間に振動やオーバーシュートを発生さない応答を得る。これによりシステムの応答を高速化できるが、制御入力が急激に変化するため、駆動部への過負荷や騒音発生などの問題が発生する場合がある。また、制御対象の非線形性やノイズの影響に弱いため、制御対象によっては適用困難な場合があることに注意が必要である。
この問題を解決する手法としてロバストデッドビート制御などが提案されている。
デッドビート応答【例】
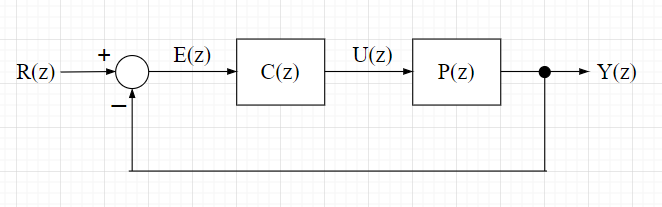
デッドビート制御
単位フィードバック制御系におけるデッドビート制御を考える。制御対象を一次遅れ系で$$P(s)=\frac{a}{s +a }$$とするとき、零次ホールド回路を使った離散時間系のパルス伝達関数\(P(z)\)は$$P(z) = \frac{1-T}{z -T} \;\;\;\; ,\;T= e^{-a\tau} $$ \(\tau\)はサンプリング時間で、$$\;\;\;0 \lt \tau \lt \infty \;\;\;, \;\;0 \lt T \lt 1$$となる。
2ステップでのデッドビート動作をさせるとすると、ステップ応答での偏差は、$$E(z) = 1 + qz^{-1} = \frac{z + q}{z} \;\;\; (q \gt 0 )$$となる。入力\(R(z)\)はステップ入力なので、$$R(z) = \frac{z}{z -1}$$また、$$E(z) = \frac{1}{ 1 + P(z)C(z)} R(z)$$なので、$$\frac{1}{1 + P(z)C(z)} = \frac{E(z)}{R(z)} = \frac{z+q}{z} \cdot \frac{z-1}{z}$$ 従って、$$P(z)C(z) = \frac{z^2 - (z +q)(z-1)}{(z + q)(z -1)}$$ 以上より、$$C(z) = \frac{z^2 - (z +q)(z-1)}{(z + q)(z -1)} \cdot \frac{1}{P(z)} = \frac{\{(1- q)z + q\}(z - T)}{(z+q)(z -1)(1-T)}$$とデッドビート制御の制御器が求まる。ここで、\(q\)はデッドビート動作時の応答経路を決めるパラメータである。\(q\)が小さいほど1スッテプ目の\(y(k)\)の立ち上がりが急峻となる。
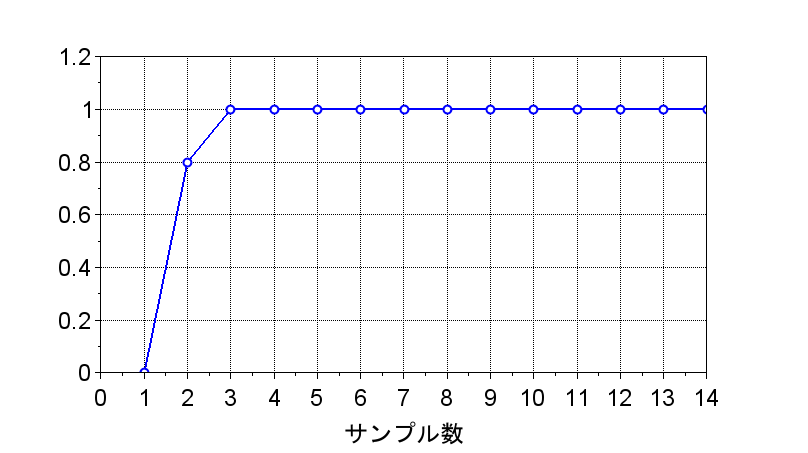
y(k)
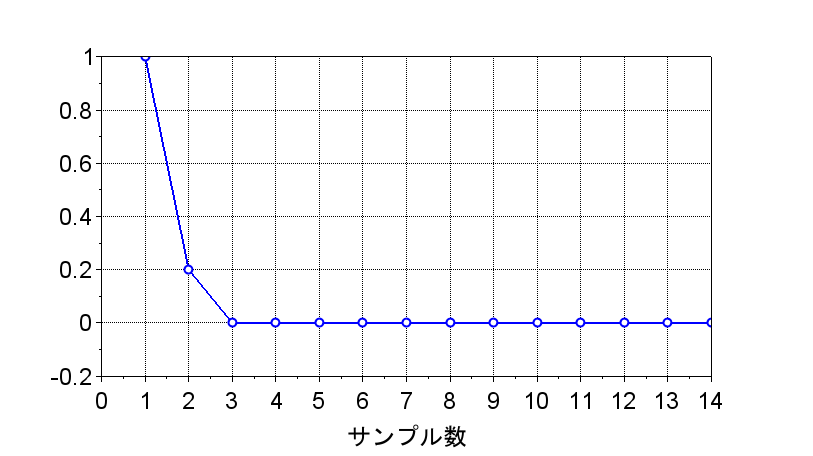
偏差e(k)
デッドビート応答【例】のScilabスクリプト
//デッドビート応答
clear; clf;
z=%z; e=%e; i=%i;
T=0.7;
P=(1-T)/(z-T);
q=0.2;
C=(((1-q)*z+q)*(z-T))/((z+q)*(z-1)*(1-T));
L=P*C; Lz=syslin('d',L);
TT=L/(1+L);
TTz=syslin('d',TT);
//ステップ応答
r=[1 1 1 1 1 1 1 1 1 1 1 1 1 1];
y = flts(r,TTz);
scf(0); plot(y , '-o');
e=r-y;
scf(1); plot(e , '-o');
この場合、特性方程式は、$$1+L(z) = \frac{z^2}{(z+q)(z-1)}=0 \;\;\;\; L(z)=P(z)C(z)$$なので、特性根(閉ループ伝達関数の極)は\(0\)の重根、つまり単位円の原点となる。
なお、このデッドビート制御ではエネルギー消費は考えていない。実際に実装できるかは別の観点からの検討が必要である。
状態フィードバックによるデッドビート制御
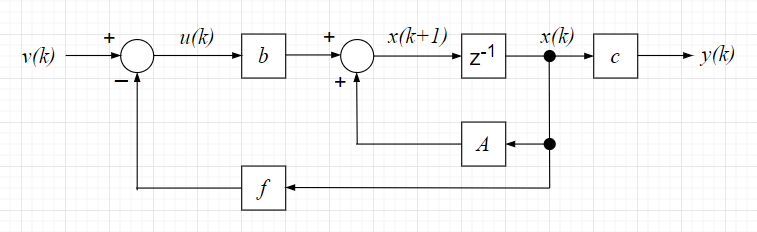
状態フィードバックを使うことで、極を任意に配置することが可能となる。デッドビート制御は、先の例で見たように極を単位円の原点にすることで実現できる。
状態フィードバックの状態空間表現は、$$x(k +1 ) = (A - bf)x(k) + b v(k)$$ $$y(k) = cx(k)$$ である。
*閉ループ系の初期値応答
状態フィードバックの閉ループ系は、\(x(k+1)=(A - bf )x(k)+b v(k)\) で、外部入力\(v(k)=0\)とすると、初期値応答は\(x(k)=(A-bf)^k x(0)\)となる。
*状態デッドビート制御問題
適当な整定数\(\nu\)が存在し、$$ (A - bf)^{\nu+i}=0 \;\;\;\; (i \ge 0)$$が成立すれば、任意の初期状態\(x(0)\)に対する応答\(x(k)\)は、有限の時間\(\nu\)で零に到達し、それ以降は零を保持するデッドビート応答となる。
※状態フィードバックで、全ての指定極をゼロにするとデッドビート制御が実現できる。
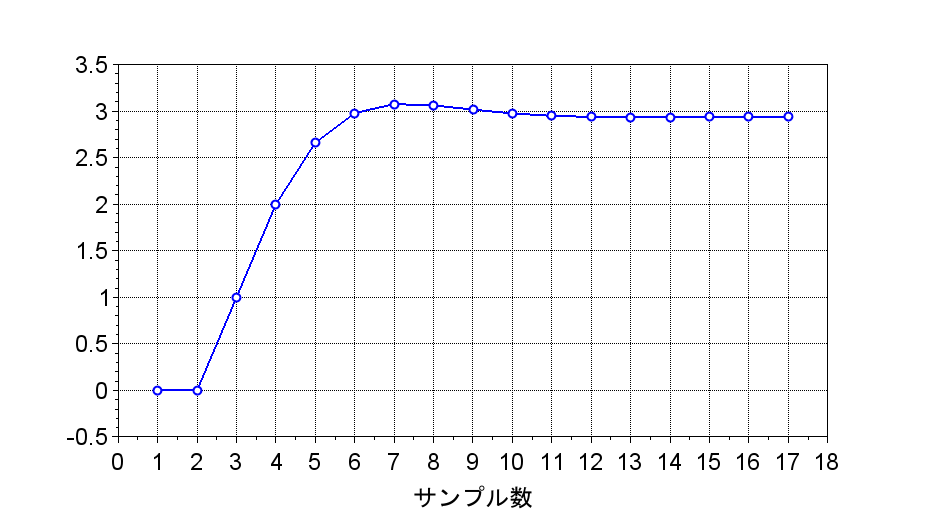
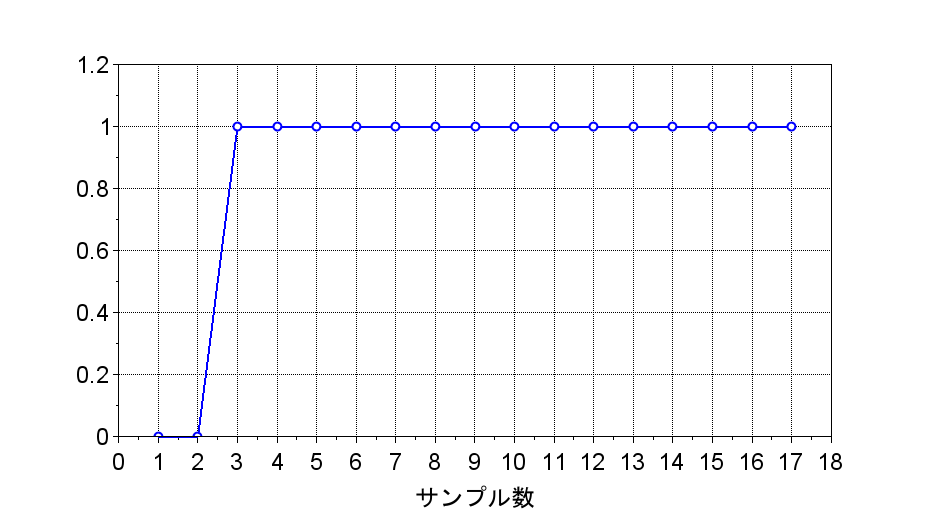
デッドビート制御のステップ応答
状態フィードバックによるデッドビート応答のScilabスクリプト
clear; clf;
z=%z; e=%e; i=%i;
A=[1 -1 ; 0 2]; b=[0 ; 1]; c=[-1 0];
//状態フィードバック系の極指定
poles=[0.5 + 0.3*i, 0.5 - 0.3*i];/*極指定*/
//フィードバックゲインの計算
F=ppol(A,b,poles);
AF=(A - b*F);
Tz=syslin('d',AF,b,c);
Tzz=ss2tf(Tz);
//ステップ応答
r=[1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1];
y = flts(r,Tzz);
scf(0); plot(y,'-o');
//デッドビート制御
poles_d=[0 ,0]; /*極指定*/
//フィードバックゲインの計算
F_d=ppol(A,b,poles_d);
AF_d=(A - b*F_d);
Tdz=syslin('d',AF_d,b,c);
Tdzz=ss2tf(Tdz);
//ステップ応答
r=[1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1];
yd = flts(r,Tdzz);
scf(1); plot(yd,'-o');
デッドビート応答と制御信号(操作量)との関係
1)デッドビート応答は、離散時間システム固有。連続時間システムではできない。
2)\(u(k)\)の大きさに制限がなければ、高々\(n\)サンプルで初期状態から零状態に移せる。
3)整定時間は高々\(nT\)なので、サンプル間隔\(T\)に依存する。\(T\)が小さければ整定時間も短いが、\(u(k)\)は大きくなる。(エネルギーが集中する)
4)サンプル間隔(設計パラメータ)は、\(u(k)\)の振幅が制限値を越えないように留意。
5)\(u(k)\)が駆動系の飽和値を越えると、デッドビート応答ではなくなり、整定時間は\(n\)サンプルより大きくなる。
※実装上、ロバスト性などの課題があり、多くの研究がある。

