4. 連続時間システムの離散化
*離散信号は、$$f^{*}(t) = \sum_{k=0}^\infty f(t) \delta(t - kT) = \left\{ f(kT) \right\} \;\;\; (k=0,1,2,\cdots)$$ \(T\):サンプリング周期(\(f_s =\frac{1}{T}\):サンプリング周波数)と表現できる。この離散時間信号\(f^{*}(t)\)はインパルス列のため、元の連続時間信号のサンプル点での情報は保持されるが、この信号は実質パワーが0であるため、この離散時間信号の状態では制御対象を駆動することはできない。従って、このインパルス列を連続時間信号に近似することが必要となる。一つの方法として、零次ホールド(Z.O.H.:Zero Order Hold)がある。
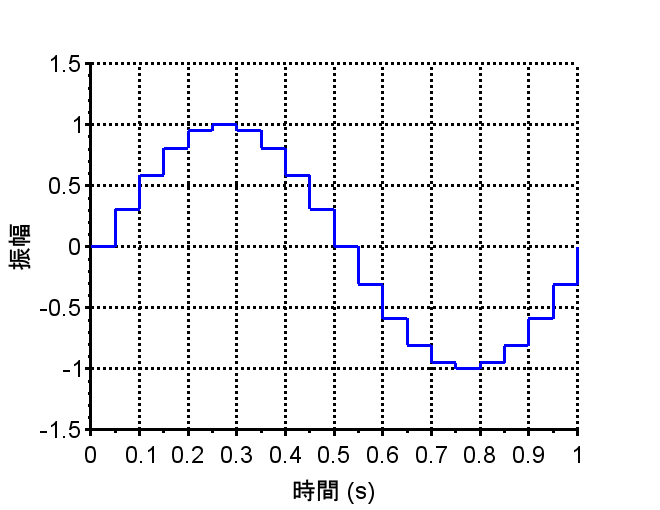
零次ホールド(Z.O.H.)
離散時間系の信号(離散時点においてのみ値を持つ信号)を連続時間系の信号(時間的に連続な信号)に変換する要素をホールドという。特に、あるサンプリング時点の値をつぎのサンプリング時点まで一定に保持することを零次ホールドという。高次のホールドもあるが、実装の容易さやサンプリング周期\(T\)を短くした場合、高次ホールドの利点がほとんど無いことから零次ホールドが最もよく用いられる。零次ホールドは、$$f(t) = f(kT) \;\;\;\;(kT \le t \lt (k+1)T) $$と表現できる。
図は、周期1秒、振幅1の正弦波を0.05秒でZ.O.H.した信号の例である。

零次ホールド回路の伝達関数
単位ステップ信号\(I(t)\)を使って、零次ホールド出力を表す。単位ステップ信号は、$$I(t)=\begin{cases} 0 \enspace \enspace (t \lt 0) \\ 1 \; \; \; (t \geq 0)\end{cases}$$なので、\(f(t) = f(kT) \;\;\;\;(kT \le t \lt (k+1)T) \)は、$$f(t)=f(kT)\left[I(t-kT) - I(t-(k+1)T\right]$$となる。従って、サンプラーによって\(f(0),f(T),f(2T), \cdots\)とサンプリングされた信号が零次ホールドに入力されたとすると、その出力\(f_H(t)\)は、$$f_H(t)=\sum_{k=0}^\infty f(kT) \left[I(t-kT) - I(t-(k+1)T\right]$$となる。
これをラプラス変換すると、$$F_H(s)=\mathcal{L}\left\{f_H(t)\right\}=\sum_{k=0}^\infty f(kT) \left\{\frac{e^{-kTs}}{s} - \frac{e^{-(k+1)Ts}}{s}\right\}$$ $$=\frac{1-e^{-Ts}}{s}\sum_{k=0}^\infty f(kT)e^{-kTs}$$となる。従って、零次ホールドの入力が\(F^{*}(s)=\sum_{k=0}^\infty f(kT)e^{-kTs}\)、出力が\(F_H(s)\)と考えて、零次ホールドの伝達関数\(H(s)\)は、$$H(s)=\frac{1 - e^{-Ts}}{s}$$と表せる。
※\(F^{*}(s)=\sum_{k=0}^\infty f(kT)e^{-kTs}\)は、インパルス列のラプラス変換で、\(z=e^{Ts}\) に置き換えるとZ変換の式(\(F(z)=\sum_{k=0}^{\infty} f(kT)z^{-k}\))が得られる。
零次ホールドの入力信号は、$$f^{*}(t)=\mathcal{L}^{-1}\left\{F^{*}(s)\right\}$$ $$=\sum_{k=0}^\infty f(kT)\delta(t-kT)=\{f(0),f(T),f(2T),f(3T),\cdots \}$$と、サンプラーによってサンプリングされた信号である。
零次ホールドの伝達関数は、\(H(s)=\frac{1 - e^{-Ts}}{s}\) で、これはs領域(連続時間系)の伝達関数である。ただし、これは有理関数ではないので、Scilabでボード線図を描くには少し工夫が必要である。具体的には \(e^{-Ts}\)の指数関数部分にPade近似を使って、周波数特性の近似を描画する。
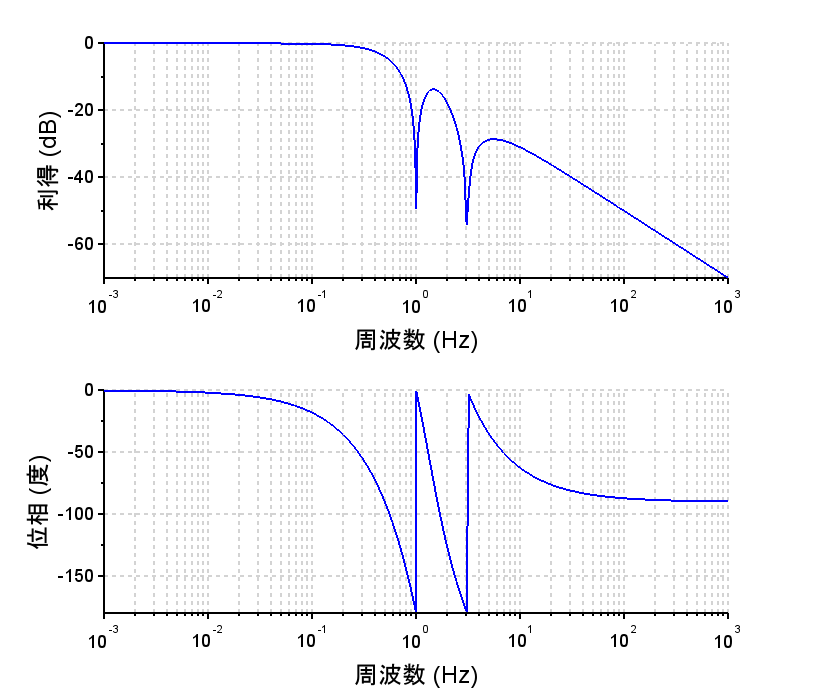
ScilabによるZ.O.H.の周波数特性
// ZOHの周波数特性
clear; clf();
s=%s;e=%e;
T=1;
//0次ホールドの伝達関数
//H=(1-e^(-T*s))/s;
// e^(-Ts)を5次のパデ近似(G)で表す
G=(-s^5/30240 + s^4/1008 - s^3/72 + s^2/9 - s/2 + 1)/(s^5/30240 + s^4/1008 + s^3/72 + s^2/9 + s/2 + 1);
H=(1-G)/s; /*ZOHの伝達関数*/
Hs=syslin('c',H);
bode(Hs);
Z.O.H.の周波数特性は、パデ近似を利用して求めた。サンプリング周期\(T=1\)[s](\(f_s=1\)[Hz])とした場合の周波数特性なので、0.5[Hz]未満の周波数帯域で良い近似になっている。
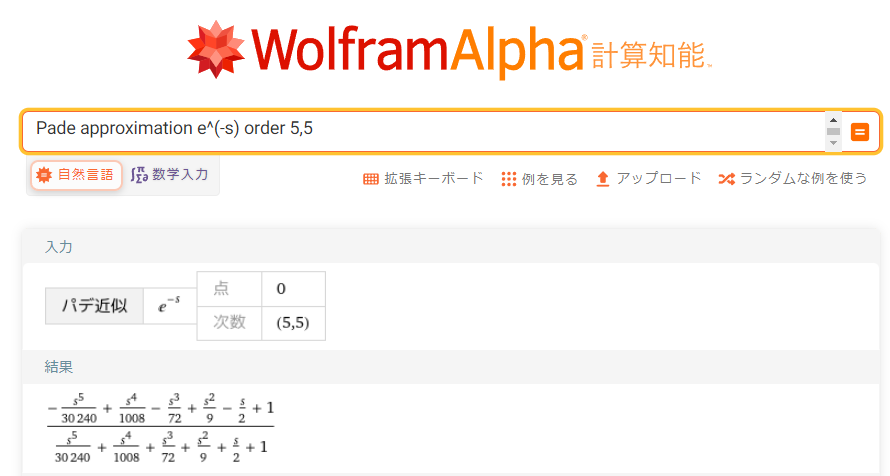
*パデ近似
パデ近似は 関数を近似する手法の一つで、2つのべき級数の比で構成される有理関数となる。例えば、むだ時間要素の伝達関数\(e^{-Ls}\)は、以下のように近似できる。
・1次のパデ近似$$e^{-Ls} \approx \frac{1 - \frac{Ls}{2}}{1 + \frac{Ls}{2}}$$ ・2次のパデ近似$$e^{-Ls} \approx \frac{1-\frac{Ls}{2} + \frac{(Ls)^2}{12}}{1+\frac{Ls}{2} + \frac{(Ls)^2}{12}}$$
※高次のパデ近似を求めるのは大変だが、https://ja.wolframalpha.com/ を使用するのも一つの手だ。結果の式は、若干の修正が必要だが、カット&ペーストでScilabのスクリプト中に挿入できるので便利だ。
連続時間システムの離散化
*状態方程式の離散化
$$\frac{d}{dt}x = Fx(t) + g u(t) \; \; \; \;\; F(n \times n), g(n \times 1)$$ $$y(t) =cx(t) \; \; \; \; \; c(1 \times n)$$ \(x(t)\)は、\(n\)次元ベクトル、また、1入力1出力システムを考えるので、\(u(t), y(t)\)はスカラーとする。
$$u(t) = u(kT) \;\;\;\;\; (kT \le t \lt (k+1)T)$$とする。(D/A出力、すなわち零次ホールドされた出力とする。)
以下、\(x(kT)=x(k)\)、\(u(kT)=u(k)\)と略した表記にする。これは、通常サンプリング周期\(T\)は、ディジタル制御器、すなわち一般に実装されるコンピュータ内の演算には無関係であるから問題ない。ただし、連続時間系に接続するときには\(T\)を考慮する必要がある。$$x(k+1) = Ax(k)+bu(k) \; \; \; \;\; A(n \times n), b(n \times 1)$$ $$y(k) =cx(k) \; \; \; \; \; c(1 \times n)$$ $$A = e^{FT} \;\;\;\;\; b=\int_0^T e^{F\tau}g d\tau$$ \(A ,\;\; b\)はサンプリング周期\(T\)の関数になる。
*パルス伝達関数
$$x(k+1)=Ax(k) + bu(k) \;\;\;\;\;\;\;\ y(k) = cx(k)$$これをZ変換すると$$zX(z) - zx_0 = AX(z) + bU(z)$$ 初期値\(x_0=0\)とすると、\(X(z)=(zI - A)^{-1}bU(z)\) また、\(Y(z) = cX(z) = c(zI - A)^{-1}bU(z)\) なので、パルス伝達関数は、$$G(z)=\frac{Y(z)}{U(z)} = c(zI - A)^{-1}b $$であり、 $$Y(z)=G(z)U(z)$$となる。
サンプル値信号がZ.O.H.されて連続時間システムに加えられる場合
サンプル値信号が零次ホールドされて連続時間システムに加えられる場合は、多くの産業機器で実装されている制御システムと言える。つまり、マイコン内臓のD/A変換器の出力が制御機器の駆動回路に加えられるような場合である。
【例】コンピュータで制御演算して、D/Aを使った出力でモータを回転させる場合の制御対象モデル
駆動回路を含めたモータの連続時間系の伝達関数を\(G(s)\)として、それにD/Aの出力を印可する。その時のD/A(零次ホールド)を含めた伝達関数は、$$G(z) = \mathcal{Z}\left\{\frac{1 - e^{-Ts}{s}}{s} G(s)\right\}$$となる。ここで、\(F(s) = \frac{G(s)}{s}\)とおくと、$$G(z) = \mathcal{Z} \left[(1 - e^{-Ts})F(s) \right] = F(z) - z^{-1} F(z)$$となる。以上より、Z.O.H.を含めた連続時間システムのパルス伝達関数は、$$G(z) = (1 - z^{-1})\mathcal{Z}\left\{\frac{G(s)}{s}\right\}$$と表せる。
サンプル・ホールドの影響
サンプル・ホールドの影響の例をシミュレーションでみる。連続時間系の伝達関数が、\(G(s)=\frac{10}{s+10}\)の一次遅れ系として、入力を零次ホールドから受けるとする。また、入力信号を\(u(t)=2t-\frac{t^2}{2}\)とする。
$$G(z)=\mathcal{Z}\left\{G(s)\right\}=\frac{1 - e^{-10T}}{z - e^{-10T}}$$で、Scilabでは、Gz=G(z)としてGzz=syslin(T,Gz)により、Z.O.H.を仮定してシステム関数に変換する。
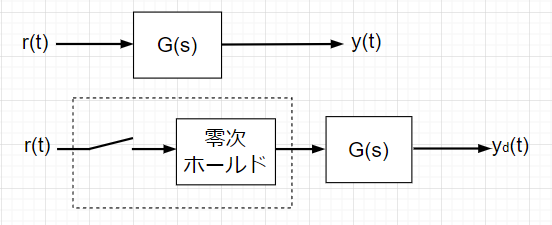
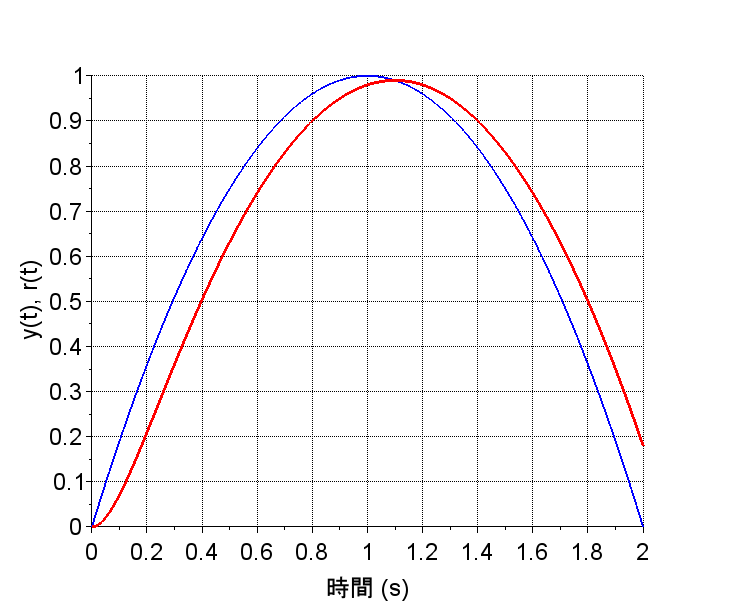
青:r(t)、赤:y(t)
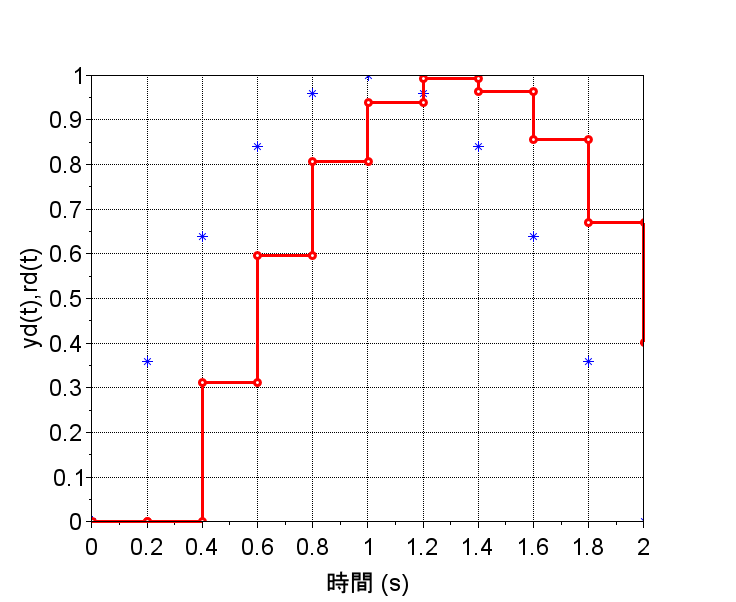
青:rd(t)、赤:yd(t)
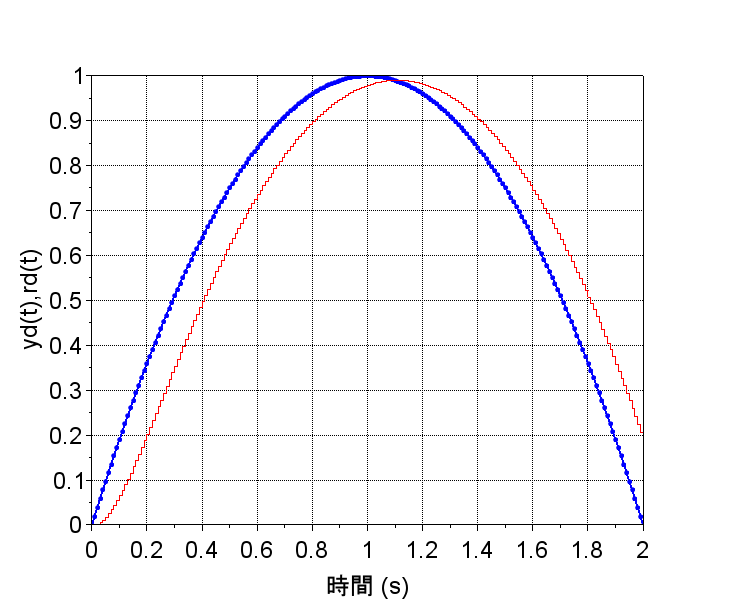
青:rd(t)、赤:yd(t)
Scilabでのシミュレーション
//サンプル・ホールドの影響
clear; clf;
s=%s; z=%z;e=%e;
G=10/(s+10); /*1次遅れ系*/
Gs=syslin('c',G);
t=0:0.001:2;
r=2*t-t^2;
y=csim(r,t,Gs); /*連続時間系の時間応答*/
scf(0);
plot2d(t,r,2);
plot2d(t,y,5);
//サンプリング周期T=0.2[s]の場合
T=0.2;
Gz=(1-e^(-10*T))/(z-e^(-10*T));
Gzz=syslin(T,Gz);
k=0:T:T*10;
rk=2*k-k^2;
yz = flts(rk,Gzz); /*離散時間系の時間応答*/
scf(1);
plot(k,rk,'*');
plot(k,yz,'ro-.');
//サンプリング周期T=0.01[s]の場合
T=0.01;
Gz=(1-e^(-10*T))/(z-e^(-10*T));
Gzz=syslin(T,Gz);
k=0:T:T*200;
rk=2*k-k^2;
yz = flts(rk,Gzz); /*離散時間系の時間応答*/
scf(2);
plot(k,rk);
plot(k,yz,'ro-.');
連続時間系の時間応答では、制御対象\(G(s)\)が1次遅れ系のため、応答に遅れが生じている。離散時間系の時間応答では、サンプリング周期\(T=0.2\)[s]の場合、サンプル・ホールドの影響でさらに遅れが生じている。これは、Z.O.H.の周波数特性から予測できることである。離散時間系の時間応答でサンプリング周期\(T=0.01\)[s]の場合、サンプル・ホールドの影響は小さくなり、連続時間系の時間応答に近くなる。


“4. 連続時間システムの離散化” に対して2件のコメントがあります。
コメントは受け付けていません。