7. 離散時間システムのインパルス応答
離散時間システムとは、時間の経過とともに変化する状態を、離散的な時間間隔で表現するシステムである。離散時間システムでは、連続時間システムとは対照的に、時間の経過を連続的な値ではなく、サンプリングされた値で扱う。
離散時間システムの主な特徴をまとめる。
1)離散時間での進行:離散時間システムでは、時間が離散的なステップで進行する。多くは、連続時間信号を離散的にサンプリングしたデータを扱う。
2)差分方程式: 連続時間システムが微分方程式を用いて表現されるのに対し、離散時間システムは差分方程式で表現されるのが一般的である。
3)サンプリング: 離散時間システムは、通常、連続時間信号を離散時間信号に変換するサンプリング操作を伴う。
4)Z変換: 離散時間システムを解析するためには、しばしばZ変換が利用される。Z変換は、差分方程式で表された離散時間システムを複素平面上で解析するための手法であり、システムの周波数応答や安定性を解析するのに役立つ。
離散時間システムには、分析と設計が容易、デジタル実装が容易、ノイズの影響が少ないなどの利点がある。一方、サンプリングによる情報損失、量子化誤差、エイリアシングなどの欠点もある。
LTIシステムのインパルス応答
離散時間信号を入出力とするシステムを離散時間システムという。
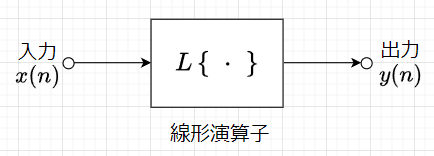
入力\(x(n)\)、出力\(y(n)\)に変換するシステムが線形であれば、線形演算子を\(L\{ \cdot \}\)として、$$L\{x(n)\} = y(n)$$と表せる(図1)。
線形システムでは重ね合わせの理が成り立つので、入力を\(x_1(n) ,\; x_2(n)\)を印可した時の出力を\(y_1(n), \; y_2(n)\)とすると、任意の定数を\(a, \; b\)として、$$L \{ a x_1(n) + b x_2(n) \} = a L \{x_1(n)\} + b L \{x_2(n)\} = a y_1(n) + b y_2(n)$$となる。
入力\(x(n)\)に対する出力を\(y(n)\)として、入力\(x(n -k)\)に対する出力が、$$L\{x( n -k)\} = y(n - k)$$を満たすシステムを時不変という。線形性と時不変性とをあわせもったシステムを線形時不変(Linear Time Invariant:LTI)システムという。
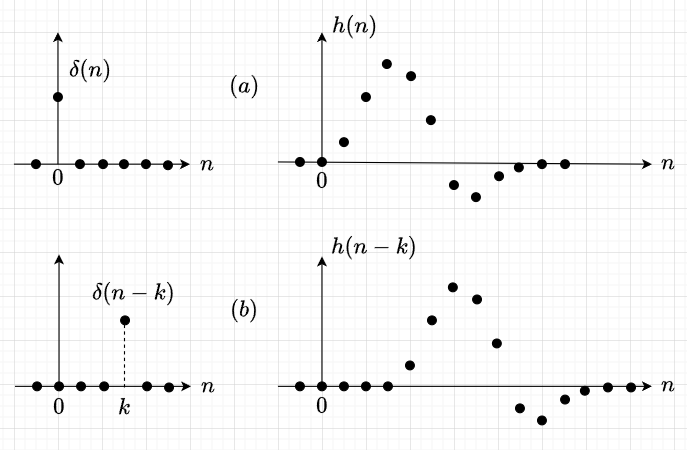
線形システムは単位インパルス\(\delta(n)\)を入力したときの応答\(h(n)\)によって記述できる。つまり、$$L\{\delta(n)\} = h(n)$$で、この関係をインパルス応答という。図2(a)にインパルス応答の例を示す。また、図2(b)に示すように、線形システムが時不変であれば、$$L\{\delta(n - k)\} = h(n - k)$$となる。
有限な入力に対する応答\(y(t)\)が有限なとき、そのシステムは安定であるという。LTIシステムが安定であるための必要十分条件は、インパルス応答\(h(t)\)が、$$\sum_{n=-\infty}^{\infty} |h(n)| < \infty$$を満たすことである。システムの応答\(y(m)\)が\(n \le m\)の入力\(x(n)\)のみによって決まるとき、そのシステムを因果性システムという。LTIシステムが因果性を満たすための必要十分条件は、インパルス応答\(h(n)\)が、$$h(n) = 0, \;\;\; n<0$$を満たすときである。
離散畳み込み和
任意の離散時間信号\(x(n)\)は、単位インパルス列を使って、$$x(n) = \sum_{k=-\infty}^{\infty} x(k) \delta(n - k)$$と表せる。この\(x(n)\)を入力とした応答\(y(n)\)は、$$y(n) = L\left\{\sum_{k=-\infty}^{\infty} x(k) \delta(n - k)\right\}$$である。ここで、線形性が成り立つとすると、$$y(n) = \sum_{k = -\infty}^{\infty} x(k) L\{\delta(n - k)\} = \sum_{k=-\infty}^{\infty} x(k) h(n - k)$$となる。これは、連続時間システムの畳み込み積分に対応した、離散畳み込み和である。さらに、システムが因果性を満たし、\(x(n) = 0, \;\;\; n<0\)ならば、$$y(n) = \sum_{k=0}^{n} x(k) h(n - k)$$である。また、離散畳み込み和を\(\ast\)を使って、$$y(n) = x(n) \ast h(n) = h(n) \ast x(n)$$と表記する。
LTIシステムの接続
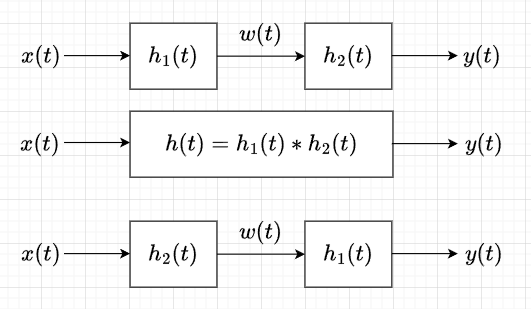
2つのLTIシステムが縦続接続されたときの応答は、図3に示すように、$$w(t) = h_1(t) \ast x(t) , \;\;\; y(t) = h_2(t) \ast w(t) \\ y(t) = h(t) \ast x(t) ,\;\;\;h(t) = h_1(t) \ast h_2(t)$$となる。つまり、それぞれのインパルス応答の畳み込みの応答に等しい。また、畳み込まれる2つの数列の順序は関係ないので、接続される順序に無関係となる。
さらに、それぞれを\(Z\)変換すると、$$W(z)=H_1(z)X(z) ,\;\;\; Y(z) = H_2(z)W(z)\\Y(z) = H_1(z) H_2(z) X(z)$$と\(Z\)変換された2つのシステムの掛け算で表せる。
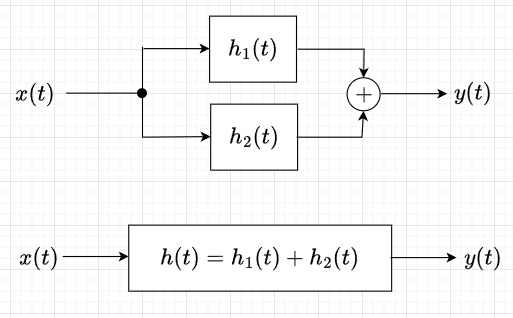
2つのLTIシステムが並列接続されたときの応答は、図4に示すように、$$y(t) = h_1(t) \ast x(t) + h_2(t) \ast x(t) \\ = \{h_1(t) + h_2(t)\}\ast x(t) \\ y(t)= h(t)\ast x(t), \;\;\;h(t) = h_1(t) + h_2(t)$$となる。つまり、それぞれのインパルス応答の和に等しくなる。
さらに、それぞれ\(Z\)変換すると、$$Y(z) = \{H_1(z) + H_2(z)\}X(z)$$である。

