6. Z変換
Z変換(Z-transform)は、離散時間信号を解析するための数学的手法であり、特に制御工学や信号処理などの分野でよく使用される。Z変換は、離散時間信号を複素平面上のZ領域に変換することで、システムの動作や応答を分析する。具体的には、連続時間信号のラプラス変換が複素s平面上で行われるのに対し、離散時間信号のZ変換は複素Z平面上で行われる。
Z変換は、離散時間システムの伝達関数や周波数応答を解析するのに役立つ。また、差分方程式をZ変換することで、離散時間システムの動的な挙動を解明することができる。制御工学やディジタル信号処理の分野では、Z変換はディジタルフィルタの設計やシステムの解析、安定性の評価などに広く利用されている。
離散時間信号
連続時間信号\(x(t)\)は、一定の時間間隔\(T\)(サンプリング周期)でサンプリングすることによって、サンプル値信号\(x_s(t)\)の系列\(\{x(n T)\}\)の離散時間信号として取り出せる。サンプリング周期\(T\)を一定とすると、離散時間信号の系列を\(\{x(n T)\} = \{x(n)\}\)と表して、\(\{x(n)\}\)を数列\(x(n)\)、\(x(k)\)を\(k\)番目の標本値と称する。\(x(k)\)は、非整数の\(k\)に対して定義されていないので、\(x(k)\)と\(x(k+1)\)の間の信号は不明となる。つまり、サンプル点間の信号の振る舞いは、このままでは扱えないことに注意しなければならない。
単位インパルス数列
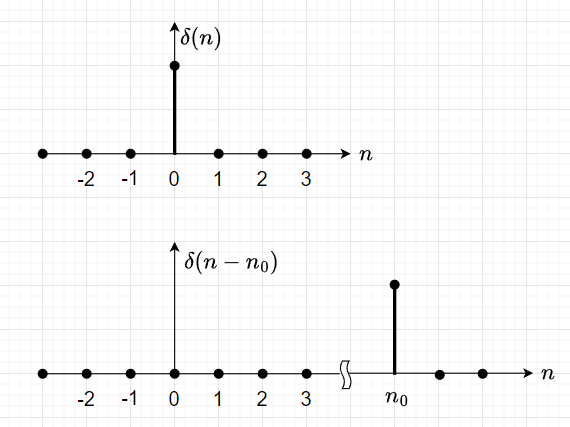
単位インパルス数列\(\delta(n)\)(クロネッカーの\(\delta\)関数)は、$$\delta(n) = \begin{cases} 1 , \enspace n = 0 \\ 0 , \enspace n \ne 0 \end{cases}$$と定義される。図1に単位インパルス数列を示す。シフトした場合(図1の下図)は、$$\delta( n - n_0) = \begin{cases} 1, \enspace n = n_0 \\ 0, \enspace n \ne n_0 \end{cases}$$と表せる。
単位ステップ数列
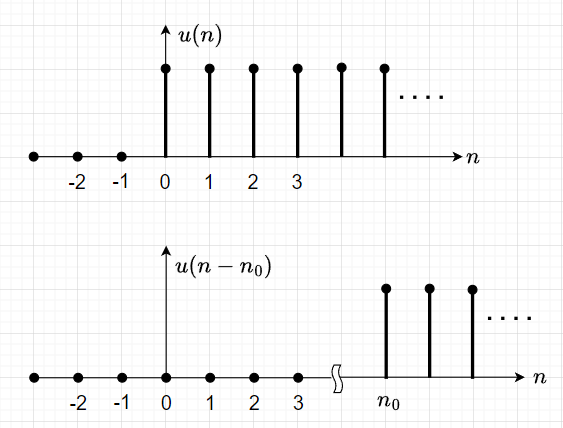
図2に単位ステップ数列を示す。単位ステップ数列\(u(n)\)は、$$u(n) = \begin{cases} 1 , \enspace n \ge 0 \\ 0 , \enspace n < 0 \end{cases}$$と定義される。シフトした場合(図2の下図)は、$$u( n - n_0) = \begin{cases} 1, \enspace n \ge n_0 \\ 0, \enspace n < n_0 \end{cases}$$と表せる。
単位インパルス数列と単位ステップ数列の間には、次式の関係がある。$$\delta(n) = u(n) - u(n-1) \\ u(n) = \sum_{k=-1}^n \delta(k)$$また、一般の数列\(x(n)\)は、単位インパルス数列\(\delta(n)\)を用いて、$$x(n) = \sum_{k = -\infty}^{\infty} x(k) \delta(n -k)$$と表せる。
指数数列
指数数列は、$$x(n) = C\cdot \alpha^n$$で表される。ここで、\(C \;\;,\alpha\)は任意の実定数とする。\(C\)を正の実定数とすると、\(\alpha\)によって、様々な形をとる。この数列は、システムの安定性を考えるとき重要となる。図3に\(\alpha\)の違いによる指数数列の例を示す。
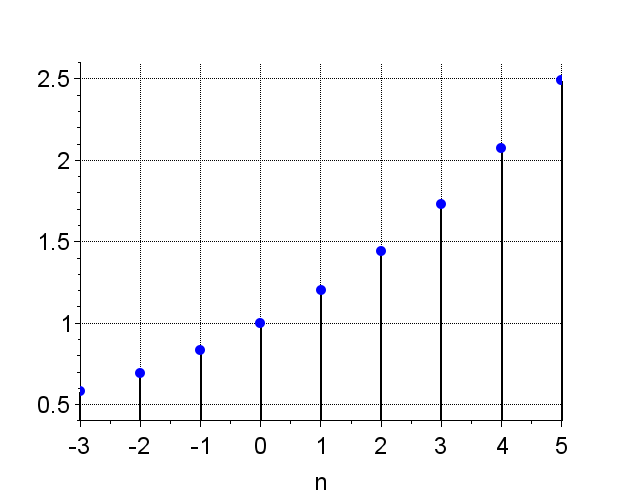
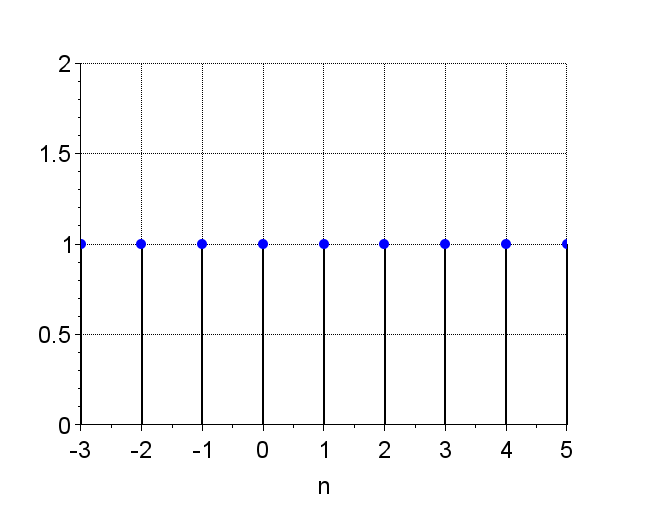
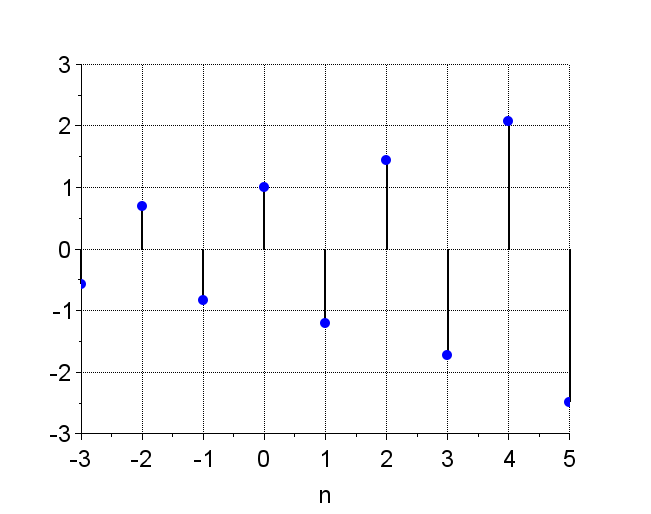
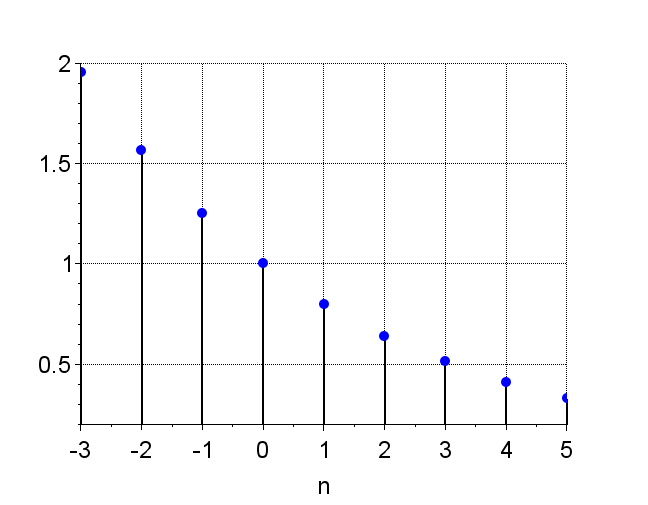
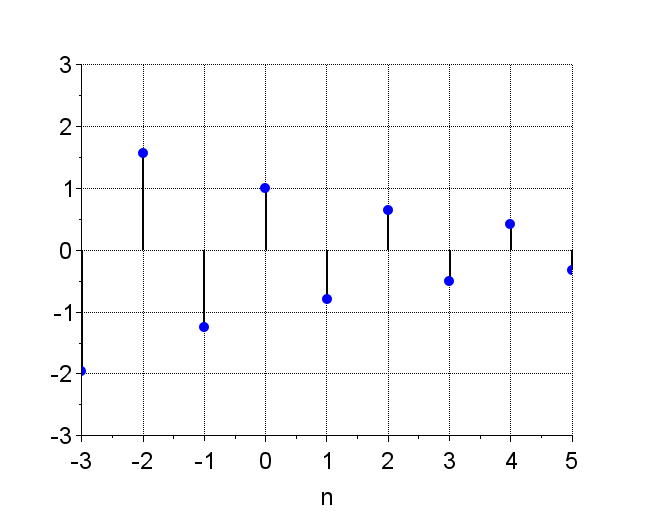
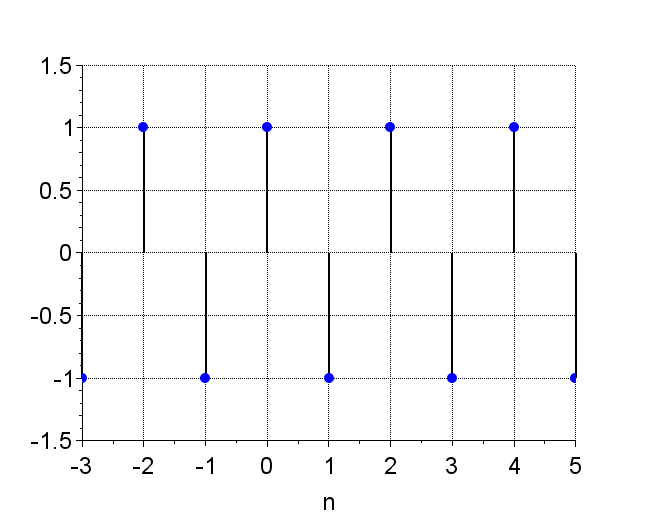
図3 指数数列の例
\(Z\)変換
因果性を有するサンプル値信号\(x_s(t)\)は、連続時間信号\(x(t)\)と単位インパルス列\(delta_T(t)\)の積によって、$$x_s(t) = x(t)\delta_T(t) \\= x(t)\delta(t) + x(t)\delta(t - T) + x(t)\delta(t - 2T) + \cdots$$と表せる。この式のラプラス変換\(X_s(s)\)を求めると、$$X_s(s) = \int_0^{\infty} \{x(t)\delta(t) + x(t)\delta(t - T) + x(t)\delta(t - 2T) + \cdots\}e^{-st}dt$$となる。インパルス関数の性質を使い、項別積分を行うと$$X_s(s) = x(0) + x(T)e^{-Ts} + x(2T)e^{-2Ts} + \cdots \\=\sum_{0}^{\infty} x(nT)e^{-nTs}$$となる。ここで、\(z=e^{sT}\)と定義すると、$$X(z) = \sum_{n=0}^{\infty} x(n)z^{-n} = \mathcal{Z}\{x(n)\} \; \cdots \cdots (1)$$と書け、この\(X(z)\)を離散時間信号\(x(nT)=x(n)\)の\(\ Z \)変換という。因果性を有する数列に対する式(1)を片側\(Z\)変換という。非因果性の数列に対しては、$$X(z) = \sum_{n=-\infty}^{\infty} x(n)z^{-n} = \mathcal{Z}\{x(n)\} \; \cdots\cdots (2)$$となり、これを両側\(Z\)変換という。なお、\(z=e^{sT}\)は複素変数なので、\(X(z)\)は一般に複素数となる。
\(Z\)変換は全ての数列に対して収束するとは限らない。また、全ての\(z\)の値に対して収束するとは限らない。式(2)が収束するのは、その数列が次式に示す絶対加算可能のときである。$$\sum_{-\infty}^{\infty} |x(n)z^{-n}| = \sum_{n=-\infty}^{\infty} |x(n)||z^{-n}| < \infty$$
\(X(z)\)が有理関数、すなわち\(z\)の多項式の比になっている場合、$$X(z) = \frac{a_0 + a_1 z^{-1}+ a_2 z^{-2} + \cdots + a_p z^{-p}} {b_0 + b_1 z^{-1} + b_2 z^{-2} + \cdots + b_q z^{-q}} = \frac{N(z)}{D(z)}$$と表せる。ここで、\(N(z) = 0\) となる\(z\)の値を零点、 \(D(z) = 0\)となる\(z\)の値を極という。一般に因果性を満たすので、\(p < q\)であり、整数\(q\)を\(X(z)\)の次数という。
単位インパルス数列の\(Z\)変換
$$X(z)=\sum_{n=0}^{\infty} \delta(n)z^{-n} = \delta(0) z^{-0} = 1$$となる。従って、収束領域は\(z\)平面全体となる。
単位ステップス数列の\(Z\)変換
$$X(z)=\sum_{n=0}^{\infty} u(n) z^{-n} = \sum_{n=0}^{\infty} z^{-n} = \frac{1}{1 - z^{-1}} = \frac{z}{z-1} , \; \enspace |z|>1$$となるので、\(|z|>1\)であれば収束する。従って、収束領域は\(|z|>1\)、すなわち複素平面の単位円の外側となる。
\(x(n) = a^n u(n) \;\;\;\;\; n\ge 0\)の\(Z\)変換
$$X(z) = \sum_{n=0}^{\infty} a^n z^{-n} = \sum_{n=0}^{\infty} (az^{-1})^n = \frac{1}{1 - a z^{-1}} = \frac{z}{z - a} , \;\;\;\;\; |z| > |a|$$となるので、\(X(z)\)は\(z=0\)に1つの零点、\(z = a\)に1つの極をもつ。収束領域は\(|z| > |a|\)、すなわち複素平面の半径\(a\)の円の外側となる。
指数数列\(x(n) = e^{-anT}u(n)\)の\(Z\)変換
1)\(a\)が実数のときは、$$X(z) = \sum_{n=0}^{\infty} e^{-anT} z^{-n} = \sum_{n=0}^{\infty} (e^{-aT} z^{-1})^n \\= \frac{1}{1 - e^{-aT}z^{-1} } = \frac{z}{z - e^{-aT}} , \enspace |z| > e^{-aT}$$である。
2)\(a\)が虚数のときは、$$X(z) = \frac{1}{1 - e^{-aT}z^{-1}} = \frac{z}{z- e^{-aT}}, \enspace |z|>1$$である。
\(x(n) = e^{-a n T}u(n)\)の\(Z\)変換は、\(a\)が実数と虚数で結果は同じであるが、収束領域が異なる。
\(Z\)変換の性質
線形性
\(x_1(n) \Leftrightarrow X_1(z)\)、\(x_2(n) \Leftrightarrow X_2(z)\)のとき、\(a,\;\;b\)を任意の定数として、$$a x_1(n) + b x_2(n) \Leftrightarrow a X_1(z) + b X_2(z)$$が成立する。
推移定理
\(x_(n) \Leftrightarrow X_(z)\)のとき、信号\(x(n -m)\)の\(Z\)変換は、$$x(n - m) \Leftrightarrow z^{-m} X(z)$$である。
指数数列の積
\(x_(n) \Leftrightarrow X_(z)\)のとき、指数数列\(e^{-anT}\)との積\(e^{-anT} x(n)\)の\(Z\)変換は、$$e^{-anT} x((n) \Leftrightarrow X(e^{aT} z)$$である。
畳み込み演算
\(x_1(n)\)、\(x_2(n)\)が因果性の信号であれば、畳み込み演算は、$$y(n) = \sum_{k=0}^{\infty} x_1(k) x_2(n - k)$$となり、\(x_1(n) \Leftrightarrow X_1(z)\)、\(x_2(n) \Leftrightarrow X_2(z)\)とすると、$$y(n) \Leftrightarrow X_1(z) X_2(z)$$が成立する。
\(Z\)変換もラプラス変換と同様に時間領域の畳み込み演算の\(Z\)変換は、複素領域での積となる。
※代表的な離散時間信号に対する\(Z\)変換の表を示す。
逆\(Z\)変換
式(3)に示す逆\(Z\)変換により、\(Z\)変換された\(X(z)\)から離散時間信号の数列\(x(n)\)を求めることができる。$$\mathcal{Z}^{-1} [X(z)] = x(n) = \frac{1}{2 \pi j}\oint_C X(z) z^{n-1} dz \cdots \cdots (3)$$ ここで、積分路\(C\) は\(X(z)\)の収束領域内にあり、原点を囲む反時計方向にまわる閉路である。
\(Z\)変換は、$$X(z) = \sum_{n=-\infty}^{\infty} x(n) z^{-n}$$なので、この式の両辺に\(z^{k-1}\)を掛けて、原点を囲み\(X(z)\)の収束領域内にある閉路\(C\)に沿って積分を行う。
コーシーの積分定理
$$\frac{1}{2 \pi j} \oint_C z^{k-1}dz = \delta(k) = \begin{cases} 1, \;\;k=0 \\ 0, \;\; k \ne 0 \end{cases}$$
$$\frac{1}{2 \pi j}\oint_C X(z) z^{k-1}dz = \frac{1}{2 \pi j} \oint_C \sum_{n=-\infty}^{\infty} x(n) z^{-n+k-1} dz$$ここで、級数部分が収束するならば、右辺の積分と累和の順序は交換できるので、$$\frac{1}{2 \pi j}\oint_C X(z) z^{k-1}dz = \sum_{n= -\infty}^{\infty} x(n) \frac{1}{2 \pi j} \oint_C z^{-n+k-1}dz$$ とでき、コーシーの積分定理を使うと、$$\frac{1}{2 \pi j}\oint_C X(z) z^{k-1} dz = x(k)$$が成立する。
留数定理による逆\(Z\)変換の計算
\(X(z)\)が有理関数であれば、式(3)の閉路積分は留数定理で比較的簡単に求まる。閉路\(C\)の内部における\(X(z) z^{n-1}\)の極の留数を\(R_k \;(k=1,2, \cdots \cdots, K)\)とすると、$$x(n) = \frac{1}{2 \pi j}\oint_C X(z) z^{n-1} dz = \sum_{k=1}^{K} R_k$$が成り立つ。\(K\)は全ての留数の個数である。\(X(z) z^{n-1}\)が\(z\)の有理関数ならば、$$X(z) z^{n-1} = \frac{N(z)}{(z -z_0)^m}$$と表せる。\(X(z) z^{n-1}\)は\(z=z_0\)に\(m\)重根(重極)を持ち、\(N(z)\)は\(z=z_0\)の根(零点)を持たない。つまり、極零相殺は無いとする。このとき、\(z=z_0\)における\(X(z) z^{n-1}\)の留数は、式(4)から求められる。$$\textrm{Res}[X(z) z^{n-1}]_{z=z_0} = \frac{1}{(m-1)!}\left[\frac{d^{m-1}}{d z^{m-1}}N(z) \right]_{z=z_0} \cdots\cdots (4)$$
べき級数法による逆\(Z\)変換の計算
\(X(z)\)が有理関数であれば、連続除算を行うことで、\(X(z)\)は$$X(z) = a_0 +a_1 z^{-1} + a_2 z^{-2} + \cdots\cdots $$とべき級数の形で表せる。一方、\(Z\)変換の定義式から、$$X(z) = \sum_{n=0}^{\infty} x(n) z^{-n} = x(0) + x(1) z^{-1} + x(2) z^{-2} + \cdots \cdots$$なので、この2式を比較すると、べき級数の係数\(a_n\)と数列の値\(x(n)\)が対応していることが分かる。従って、$$x(n) = a_n, \;\;\; n \ge 0$$と逆\(Z\)変換が求まる。
部分分数展開法による逆\(Z\)変換の計算
この方法は、留数定理による方法と本質的には差が無いが、一般的な\(X(z)\)の場合、計算が少し分かりやすい。
\(Z\)変換表より、\(z^{-m}\)および、\(\frac{z}{(z-p)^m}\)の形の関数については逆\(Z\)変換が分かっているので、以下の形になるように部分分数展開する。$$X(z) = a_0 + \frac{a_1}{z} + \frac{a_2}{z^2} + \cdots + \frac{b_1 z}{(z - p_1)} + \frac{b_2 z}{(z - p_1)^2} + \cdots + \frac{c_1 z}{(z - p_2)} + \frac{c_2 z}{(z - p_2)^2} + \cdots $$これにより、\(Z\)変換の線形性と\(Z\)変換表を使って、$$x(n) = a_0 \delta(n) + a_1 \delta(n-1) + a_2 \delta(n-2) + \cdots + b_1 p_1^n+ b_2 n p_1^{n-1} + \cdots + c_1 p_2^n + c_2 n p_2^{n-1} + \cdots $$が得られる。この部分分数展開は、各項の分子に\(z\)がのっていることに注意が必要である。この形の展開形を得るには、\(\frac{X(z)}{z}\)を通常の部分分数展開して、後に両辺に\(z\)を掛ければよい。
【例】$$X(z) = \frac{z}{3 z^2 - 4 z + 1}$$を逆\(Z\)変換する。
まず、\(X(z)/z\)の部分分数展開を求める。
$$\frac{X(z)}{z} = \frac{1}{(z -1)(3 z -1)} = \frac{A}{z-1} + \frac{B}{3z -1}$$ \(A,\;B\)は、$$A = \left. (z-1)\frac{X(z)}{z} \right|_{z=1} = \frac{1}{2} \\ B = \left. (3 z -1)\frac{X(z)}{z} \right|_{z=1/3} = -\frac{3}{2}$$よって、$$X(z) = \frac{1}{2} \left(\frac{z}{z-1} - \frac{z}{z - 1/3} \right)$$が得られる。各項の逆\(Z\)変換は、$$\mathcal{Z}^{-1} \left(\frac{z}{z-1}\right) = 1, \;\;\;\;\; \mathcal{Z}^{-1} \left(\frac{z}{z-1/3}\right) = \left(\frac{1}{3}\right)^n$$である。従って、$$x(n) = \frac{1}{2} ( 1 - 3^{-n})$$となる。

