18. サーボシステムの設計
レギュレータは、状態変数に平衡点0からずれた初期値があったとき、状態変数を0に戻すための制御システムであった。サーボシステムは、目標値に追従する出力を持つシステムである。現代制御理論におけるサーボシステムの設計は、システムの状態方程式に基づいて行われる。状態方程式に基づいて、システムの特性(安定性、応答速度、精度など)を評価し、コントローラを設計する。
サーボシステムの設計は、複雑な問題であるが、現代制御理論を用いることで、システムの特性を改善し、目的に応じたサーボシステムを設計することができる。
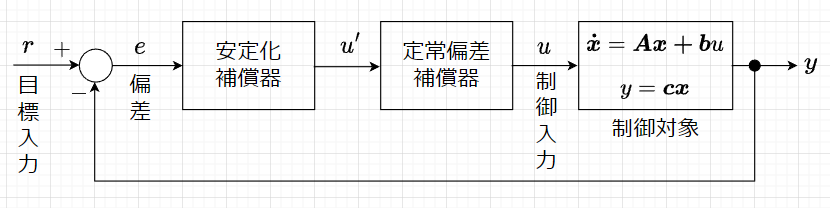
サーボシステムでは、目標入力と呼ばれる希望の時間関数に出力を追従させる。このためには、単に閉ループシステムの安定化以外に、平衡点の制御が必要になる。また、制御できる状態変数の数も入力変数の数によって制限される。平衡点の制御には積分動作を利用する。
ここでは、制御対象を1入力1出力システム$$\boldsymbol{\dot{x}}(t) = \boldsymbol{Ax}(t) + \boldsymbol{b}u(t) \;\;\; :\boldsymbol{A}\;(n \times n),\; \boldsymbol{b}\;(n \times 1) \\ y(t) = \boldsymbol{cx}(t) \;\;\;: \boldsymbol{c}\;(1 \times n)$$とし、可制御、可観測とする。ここで、\(y(t)\)は目標入力\(r(t)\)に追従させたい出力であり、測定可能な出力とする。
サーボシステムではレギュレータの場合と異なり、図「サーボシステムの構成」のように出力と目標入力との偏差\(e(t)=r(t)-y(t)\)を制御用の信号とする。とくに、偏差の定常値\(e(\infty)\)を定常偏差という。サーボシステムでは、閉ループシステムが漸近安定で、かつ、定常偏差が小さいか、零になることが設計仕様となる。定常偏差が零になるということは、\(y(t)\)が\(r(t)\)に一致することを意味する。この制御仕様を満たすためには、図「サーボシステムの構成」にあるように、定常偏差補償器と安定化補償器が必要となる。
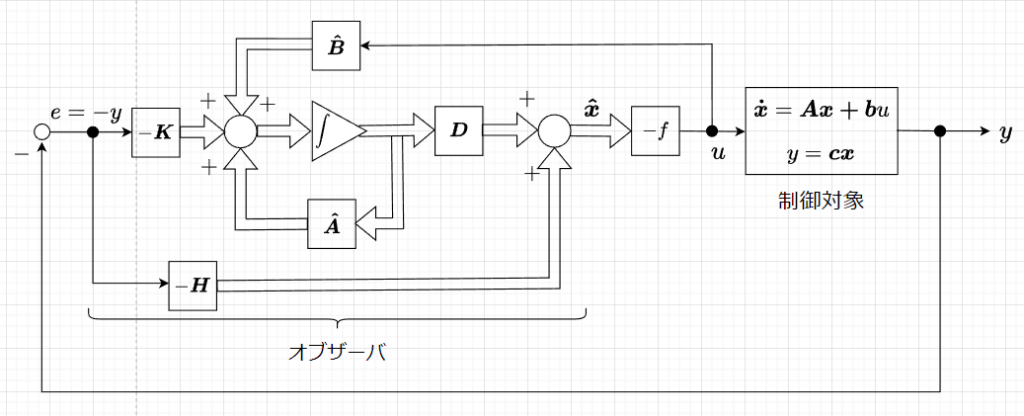
サーボシステムにおいて目標入力\(r(t)=0\)とすると、そのシステムはレギュレータとなる。この場合、閉ループシステムを漸近安定にできれば、任意の初期値に対して\(\boldsymbol{x}(\infty)=\boldsymbol{0}\)となるので、\(y(\infty)=0\)となり、定常偏差補償器を不要となる。このときのオブザーバ併合レギュレータは、図「オブザーバ併合レギュレータ」のように表せるので、安定化補償器としてオブザーバが用いられる。(古典制御理論におけるPID制御器や位相進み補償器はこのオブザーバのような機能を持っている。)
このオブザーバによる安定化補償器の伝達関数を\(G_d(s)\)とし、また、定常偏差補償器の伝達関数を\(G_s(s)\)とする。
定常偏差と開ループシステムの型
※定常偏差に関しては、基礎制御工学の27. 定常特性と内部モデル原理を参考にして欲しい。
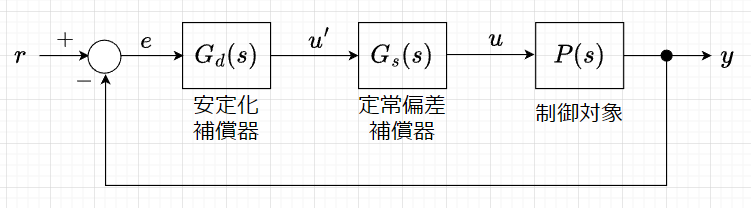
図「サーボシステムの伝達関数表現」より、開ループシステムの伝達関数は、$$L(s) = P(s)G_s(s)G_d(s)$$となる。従って、サーボシステム(図「サーボシステムの構成」参照)は、図「単位フィードバックシステム」に示す閉ループシステムで表せる。
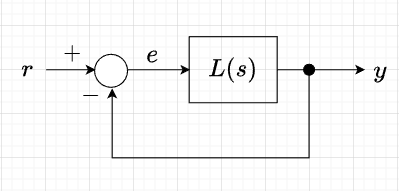
偏差\(e(t)\)のラプラス変換は\(E(s)\)で、偏差と目標入力の関係は、$$E(s)=R(s)-Y(s) \;\;\;\;\; Y(s)=L(s)E(s) \;\;\;\;\; E(s) = R(s) - L(s) E(s) \\E(s) = \frac{1}{1 + L(s)}R(s)$$と表せる。
目標入力として、よく用いられる時間関数$$r^i(t)=0 \;\;(t \lt 0), \;\;\;\;r^i(t)=\frac{a_i}{i!}t^i \;\;\;(t \ge 0)$$で考える。 これをラプラス変換すると、$$R^i(s) = \frac{a_i}{s^{i+1}}$$となる。ここで、\(i \ge 0\)で、\(a_i\)は任意の係数である。\(i=0\)であればステップ関数、\(i=1\)であればランプ関数、\(i=2\)であればパラボラ関数である。この目標入力に対する偏差は、$$E^{i}(s) = \frac{1}{1 + H(s)}\cdot \frac{a_i}{s^{i+1}}$$となる。閉ループシステムが漸近安定とすると、ラプラス変換の最終値定理より、$$e^i(\infty) = \lim_{s \rightarrow 0} s E^i(s) = \lim_{s \rightarrow 0} \frac{1}{1+H(s)}\cdot \frac{a_i}{s^i} = \left\{ \begin{array} {} \displaystyle \frac{a_0}{1 + K_0} \;\;\;(i=0) \\ \frac{a_i}{K_i} \;\;\;(i \ge 1) \end{array} \right.$$ここで、$$K_i = \lim_{s \rightarrow 0} s^i H(s)$$で、\(K_i\)を定常偏差定数という。\(K_i\)が大きいほど、漸近安定な閉ループシステムにおいて、定常偏差\(e^i(\infty)\)を小さくできる。これは古典制御理論の周波数応答において、\(H(s)\)の低域ゲインが高いことに相当する。定常偏差定数が\(\infty\)となれば、定常偏差は0にできる。これを実現するためには、開ループ伝達関数\(H(s)\)が分母に\(s\)の項を持つ、すなわち、\(H(s)\)が積分要素を持つことが必要である。これを基に\(H(s)\)を分類する。$$H(s)=\frac{N(s)}{s^l D(s)} \;\;\;\; (N(0) \ne 0 , \;\;\; D(0) \ne 0) $$とすると、\(H(s)\)は、原点\(s=0\)に\(l\)個の極をもち、\(l\)型の伝達関数という。各型の\(H(s)\)に対して、以下のように整理できる。
- \(H(s)\)が0型:\(K_0 = \frac{N(0)}{D(0)},\;\;K_i=0 \;\;\;(i \ge 1) \)
- \(H(s)\)が1型:\(K_0=\infty, \;\; K_ 1= \frac{N(0)}{D(0)},\;\;K_i = 0 \;\;\;(i \ge 2) \)
- \(H(s)\)が2型:\(K_0=K_1=\infty, \;\; K_2=\frac{N(0)}{D(0)}, \;\; K_i = 0 \;\;\;(i \ge 3) \)
- \(\vdots\)
- \(H(s)\)が\(l\)型:\(K_0=K_1=\cdots=K_{l-1}=\infty, \;\; K_l=\frac{N(0)}{D(0)}, \;\; K_i = 0 \;\;\;(i \ge {l+1}) \)
\(H(s)\)が\(l\)型なら、単位フィードバックで漸近安定なシステムでは、\(e^0(\infty)= \cdots =e^{l-1}(\infty)=0, \;\; e^l(\infty)=\frac{a_i}{K_i} \ne 0, \;\; i \ge l+1 \)で\(e^i(\infty)=\infty\)となる。\(l-1\)次までの目標入力関数には出力が定常偏差なく追従し、\(l\)次関数では一定の定常偏差が生じ、\(l+1\)次以上の関数では追従できないことが分かる。
\(H(s)\)の型数が多いほど、高次の目標入力に定常偏差なしで追従できることになる。型数を多くするには、\(G_s(s)\)の積分器の段数を多くすればよいが、現実問題として、積分器を高段に実装することは困難である。また、積分器の実装では、電子回路による演算増幅器であれば電源の制約による飽和、ディジタル制御器では演算によるオーバーフローを考慮しなければならない。
サーボシステムの構成例
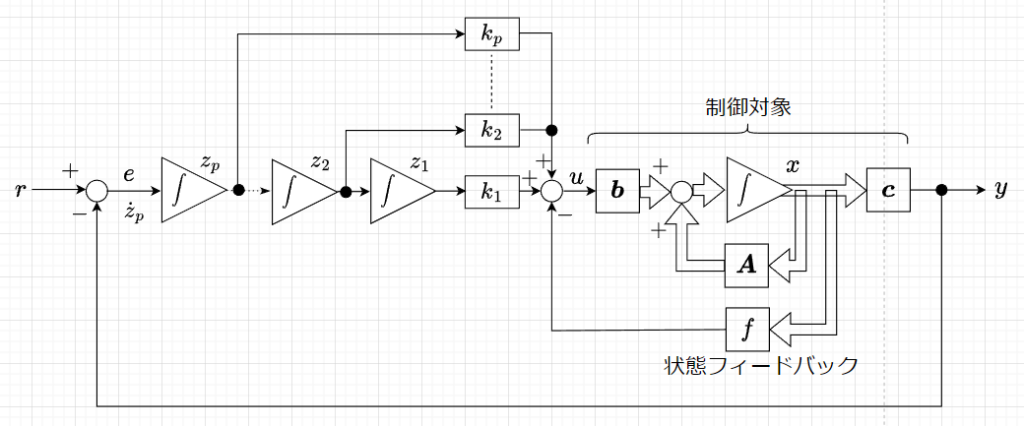
目標入力に定常偏差なく追従するために必要な型数を\(p\)とする。図「\(p\)型のサーボシステムの構成」のように、制御対象(状態フィードバックにより、安定化したシステム)の前段に\(p\)個の直列結合された積分器を置く。
これらの積分器からの前向きのゲインを\(k_1,k_2,\cdots,k_p\)とする。また、状態変数\(\boldsymbol{x}\)からの状態フィードバックゲインベクトルを \(\boldsymbol{f}\;\;(1 \times n)\)とすると、制御入力は、$$u = -\boldsymbol{fx} + k_1 z_1 + k_2 z_2 + \cdots + k_p z_p$$となる。\(r=0\)とすると、閉ループシステムは、$$\begin{bmatrix} \boldsymbol{\dot{x}} \\ \dot{z}_1 \\ \dot{z}_2 \\ \vdots \\ \vdots \\ \dot{z}_p \end{bmatrix} = \begin{bmatrix} \boldsymbol{A} & & & \boldsymbol{0} & & \\ \boldsymbol{0} & 0 & 1 & & \boldsymbol{0} & \\ \vdots & \vdots & \ddots & 1 & & \\ \vdots & \vdots & & \ddots & \ddots & \\ \boldsymbol{0} & \vdots & & & \ddots & 1\\ -c & 0 & \cdots & \cdots & \cdots & 0 \end{bmatrix} \begin{bmatrix} \boldsymbol{x} \\ z_1 \\z_2 \\ \vdots \\ \vdots \\z_p \end{bmatrix} + \begin{bmatrix} \boldsymbol{b} \\ 0 \\ \vdots \\ \vdots \\ \vdots \\ 0 \end{bmatrix} u $$ と、\(n + p\)次元のシステムで表せる。このシステムを$$\boldsymbol{\dot{\bar{x}}} = \boldsymbol{\bar{A}}\boldsymbol{\bar{x}} + \boldsymbol{\bar{b}}u, \;\;\;\; u=- \boldsymbol{\bar{f}} \boldsymbol{\bar{x}} $$とおき、\(\boldsymbol{\bar{A}} - \boldsymbol{\bar{b}}\boldsymbol{\bar{f}}\)の固有値(システムの極)を\(\mu_1,\mu_2,\cdots,\mu_{n+p}\)に設定する。この固有値は、システムを安定にするために\(\mathrm{Re}(\mu_i) \lt 0\)とする。この固有値となるように\(\boldsymbol{\bar{f}}\;(1 \times (n+p))\)を求め、$$[ \boldsymbol{f}, -k_1, -k_2, \cdots, -k_p]=\boldsymbol{\bar{f}}$$より、\(\boldsymbol{f}, k_i\)を決定する。
このサーボシステムの構成では、定常偏差補償器として、$$G_s(s) = \frac{k_p s^{p-1} + \cdots + k_2 s + k_1}{s^p}$$を直列に入れており、制御対象の型によらず、少なくとも\(p\)型となる。なお、\( (\boldsymbol{A,b})\)が可制御であれば、\( (\boldsymbol{\bar{A}}, \boldsymbol{\bar{b}})\)も可制御となる。
制御対象の状態変数が直接観測できない場合は、オブザーバを使用すればよく、このオブザーバ併合状態フィードバックが安定化補償器となる。
サーボシステムの設計【例】
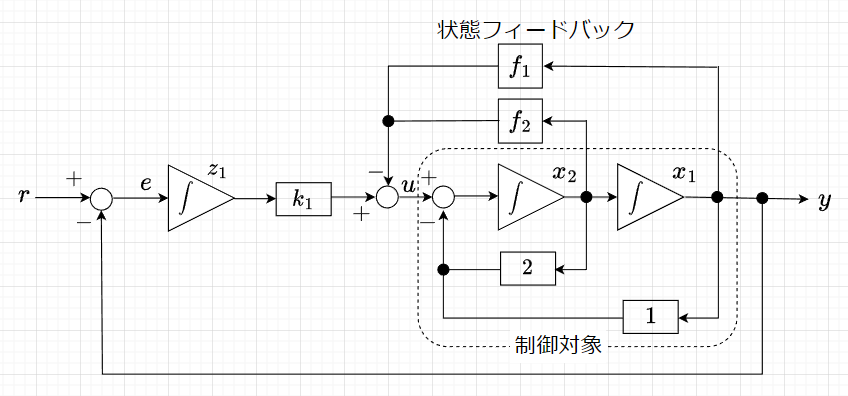
制御対象を$$\boldsymbol{\dot{x}} = \begin{bmatrix} 0 & 1 \\ -1 & -2 \end{bmatrix} \boldsymbol{x} + \begin{bmatrix} 0 \\ 1 \end{bmatrix}u \\ y = \begin{bmatrix} 1 & 0 \end{bmatrix}\boldsymbol{x}$$とする。また、状態変数\(x_1,x_2\)は直接観測可能とする。ステップ入力に定常偏差0で追従するサーボシステムを設計する。
\(r=0\)としたときの閉ループシステム(拡大システム)は、$$\begin{bmatrix} \dot{x}_1 \\ \dot{x}_2 \\ \dot{z}_1 \end{bmatrix} = \begin{bmatrix} 0 & 1 & 0 \\ -1 & -2 & 0 \\ -1 & 0 & 0 \end{bmatrix} \begin{bmatrix} x_1 \\ x_2 \\ z_1 \end{bmatrix} + \begin{bmatrix} 0 \\ 1 \\ 0 \end{bmatrix}u, \\u=-\begin{bmatrix} f_1 & f_2 & -k_1 \end{bmatrix} \begin{bmatrix} x_1 \\ x_2 \\ z_1 \end{bmatrix}$$
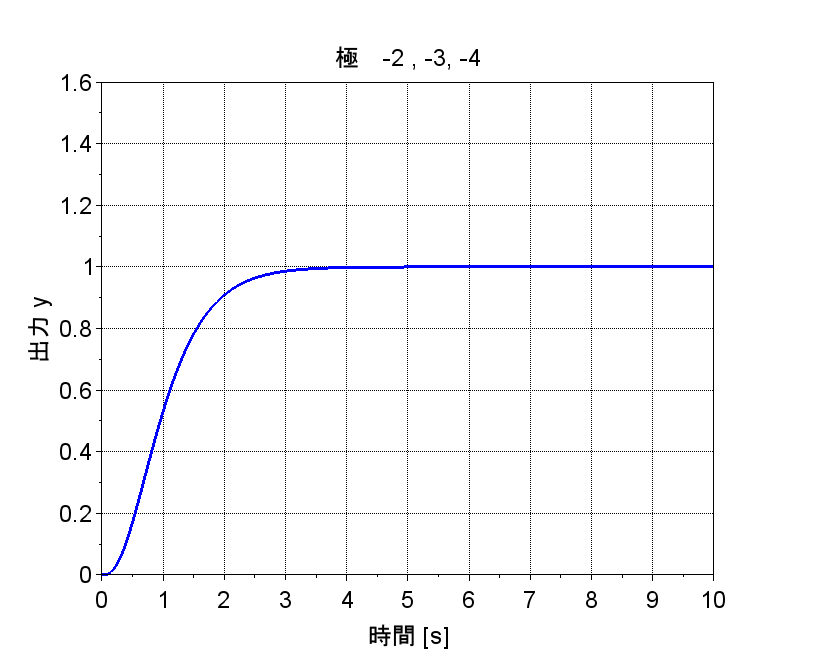
サーボシステム(1)では、極を\(-2, -3,-4\)とする。
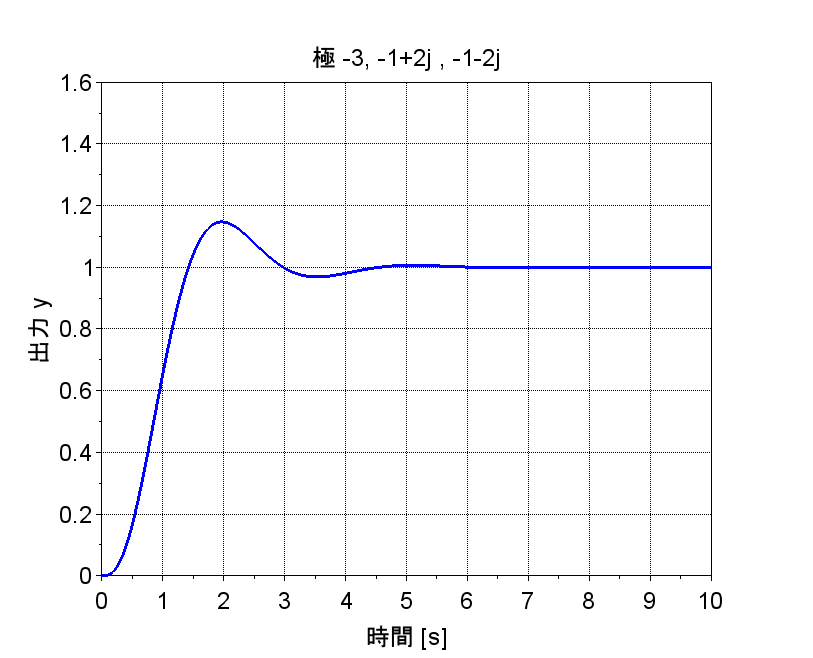
サーボシステム(2)では、極を\(-3, -1+2j, -1-2j\)とする。
Scilabスクリプト
//サーボシステムの設計
clear;clf();i=%i;
//積分器を含んだ拡大システムの定義
A=[0 1 0; -1 -2 0; -1 0 0];
b=[0; 1; 0];
c=[1 0 0];
sysP=syslin('c',A,b,c);
//拡大システムの固有値
evals=spec(A);
//可制御性のチェック
Cc=cont_mat(A,b);
n=rank(Cc);
//極配置(1)
poles=[-2 -3 -4];
//状態フィードバック係数と積分ゲインの決定
f=ppol(A,b,poles);
cpoles=spec(A-b*f); //極配置の確認
A1=A-b*f;
b1=[0; 0; 1]
sysT1=syslin('c',A1,b1,c);
//サーボシステム(1)のステップ応答
t=0:0.01:10;
y1=csim('step',t,sysT1);
scf(0);
plot(t',y1');
//極配置(2)
poles2=[-3 -1+2*i -1-2*i];
//状態フィードバック係数と積分ゲインの決定
f2=ppol(A,b,poles2);
cpoles2=spec(A-b*f2); //極配置の確認
A2=A-b*f2;
b2=[0; 0; 1]
sysT2=syslin('c',A2,b2,c);
//サーボシステム(2)のステップ応答
y2=csim('step',t,sysT2);
scf(1);
plot(t',y2');
極を\(-2, -3,-4\)としたときのステップ応答を図「サーボシステム(1)」に示す。ステップ入力に追従し、定常偏差が0となっている。極は負の実軸上であるため、ステップ応答はオーバシュートがない。
極を\(-3, -1+2j, -1-2j\)としたときのステップ応答を図「サーボシステム(2)」に示す。この場合もステップ入力に追従し、定常偏差が0となっている。極は負の実軸上の極と複素平面の左半平面の複素極であるため、ステップ応答にはオーバシュートが生じるが、目標値の1に速く到達している。以上のように、積分器を1個入れた、1型のサーボシステムの構成で極を任意に配置することで、ステップ入力に対して定常偏差を0にでき、また、希望の応答特性を実現できることがわかる。

