35. PID制御系
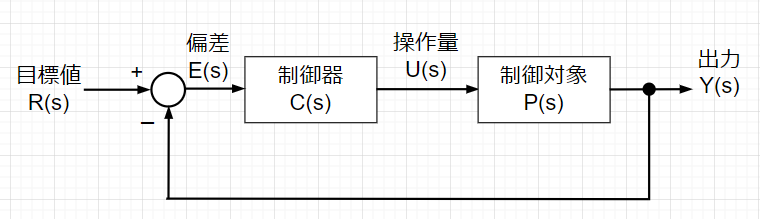
PID制御器とは、Proportional-Integral-Differential Controllerのことで、比例-積分-微分の機能を組み合わせた制御器である。(ゲイン補償、位相遅れ補償、位相進み補償を組み合わせた制御器とほぼ同等となる。)
PID制御器の要素は、以下のようにまとめられる。※ラプラス変換では初期値を\(0\)とする。
P:比例要素 \(u(t) = K_p e(t) = K_p \left (r(t)- y(t) \right)\)
ラプラス変換すると \(U(s) = K_pE(s) = K_p \left( R(s) - Y(s) \right)\)
I:積分要素 \(u(t) = K_i \int_0^t e(\tau) d\tau =K_i\int_0^\tau \left(r(\tau) - y(\tau) \right) d\tau \)
ラプラス変換すると \(U(s) = K_i \frac{E(s)}{s} = K_i\frac{R(s) - Y(s)}{s} \)
D:微分要素 \(u(t) = K_d \frac{de(t)}{dt} = K_d \frac{d\{r(t) - y(t)\}}{dt} \)
ラプラス変換すると \(U(s) = K_d sE(s) = K_d s\{R(s) - Y(s)\} \)
従って、PIDを全て組み合わせたPID制御器は、$$u(t) = K_p e(t) + K_i \int_0^t e(\tau) d\tau + K_d \frac{de(t)}{dt} $$となる。ここで、\(K_p\):比例ゲイン、 \(K_i\):積分ゲイン、 \(K_d\):微分ゲイン という。
ラプラス変換すると、$$U(s) = K_p E(s) + K_i\frac{E(s)}{s} + K_d sE(s) $$ $$= \left\{ K_p + \frac{K_i}{s} + sK_d \right\}E(s)$$なので、PID制御器の伝達関数は、$$C(s) = \frac{U(s)}{E(s)} = K_p + \frac{K_i}{s} + sK_d$$となる。式変形すると、$$C(s) = K_p + \frac{K_i}{s} + sK_d $$ $$= K_p \left\{1 + \frac{1}{T_i s} + T_ds\right\}$$となる。ここで、\(T_i = \frac{K_p}{K_i}\):積分時間、 \(T_d = \frac{K_d}{K_p}\):微分時間 という。
*\(K_p , K_i , K_d \)のパラメータ調整による時間応答特性の変化のイメージは、こちらのアニメーションを参照して欲しい。
\(K_i\)すなわち積分要素が入ると定常偏差は小さくなるが、振動的(不安定な傾向)になる。これは積分要素が位相を遅らせるため、位相余裕が減ることによる。
\(K_d\)すなわち微分要素は、位相を進めるため、積分要素で遅れた位相を補償することができる。これにより位相余裕が確保でき、良好な時間応答特性を実現できる。
PID制御器の構成
PID制御器を使用した場合、制御器\(C(s)\)は以下の式のように表せ、\(L(s) = C(s)P(s)\)は1型系になるので、プロセス制御系のような定値制御系にPID制御器を使用した場合、定常位置偏差のゼロが保証される。
$$C(s) = K_p \left\{1 + \frac{1}{T_i s} + T_ds\right\}$$ $$ = \frac{ K_p}{T_i} \left\{ \frac{T_i s + 1 + T_i T_d s^2}{ s} \right\} $$
※分子の次数が分母より高いが、一般的に制御対象は分母の次数が高い系を対象とするため、安定なシステムを構築できる。
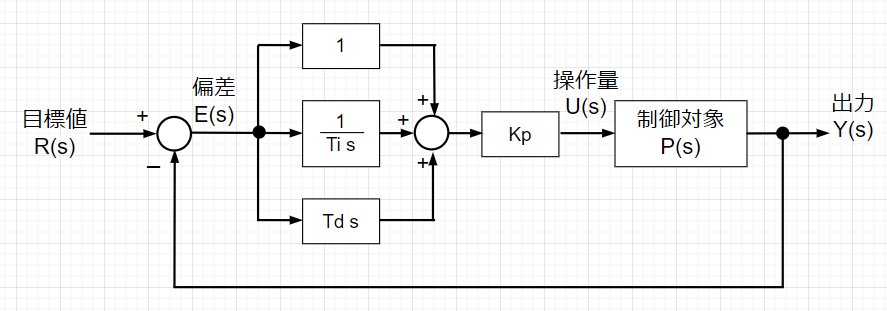
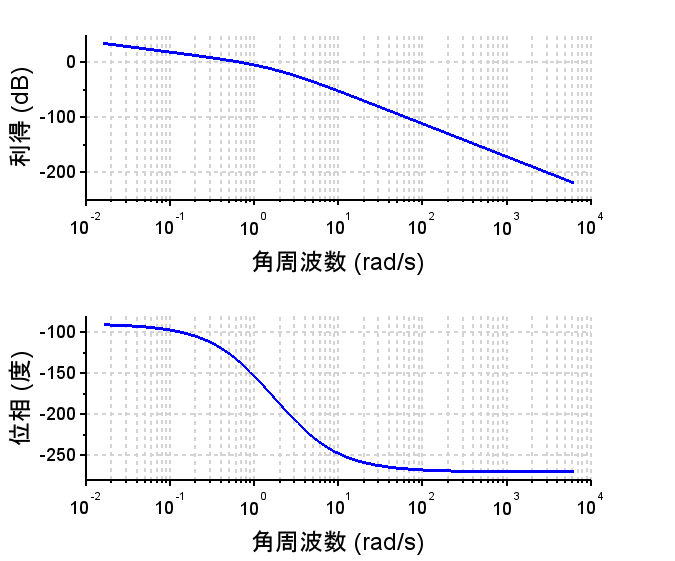
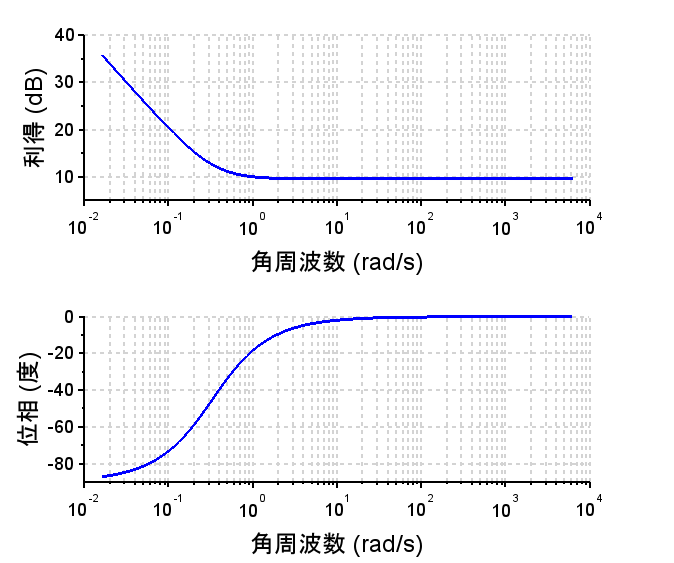
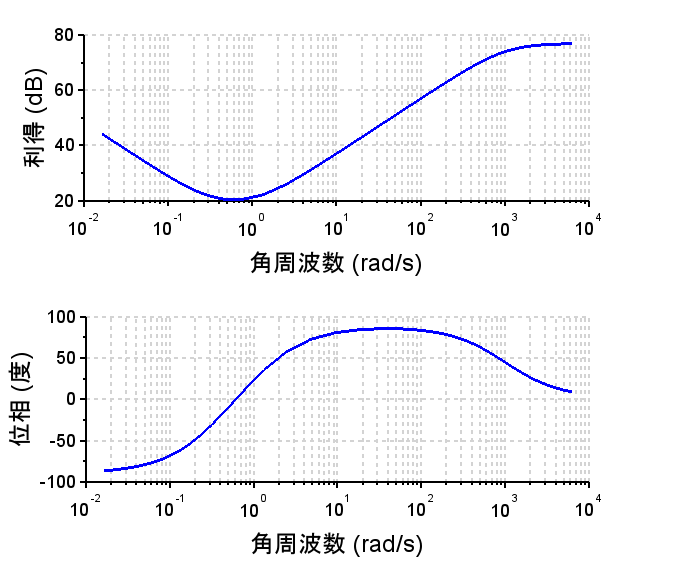
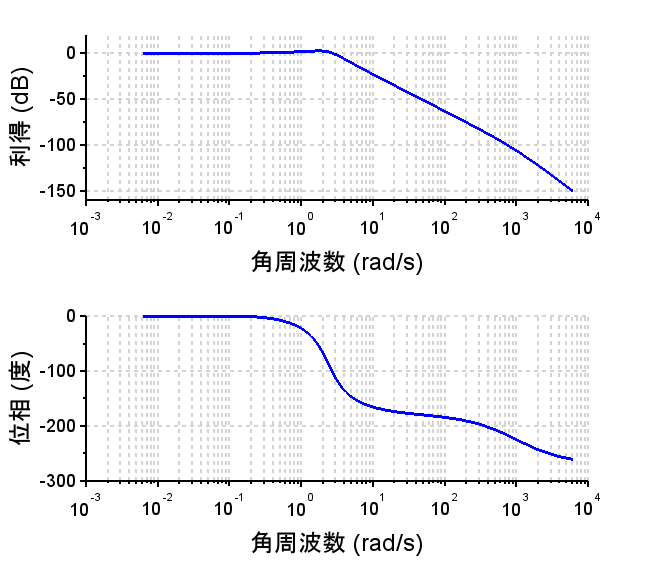
開ループ伝達関数ボード線図
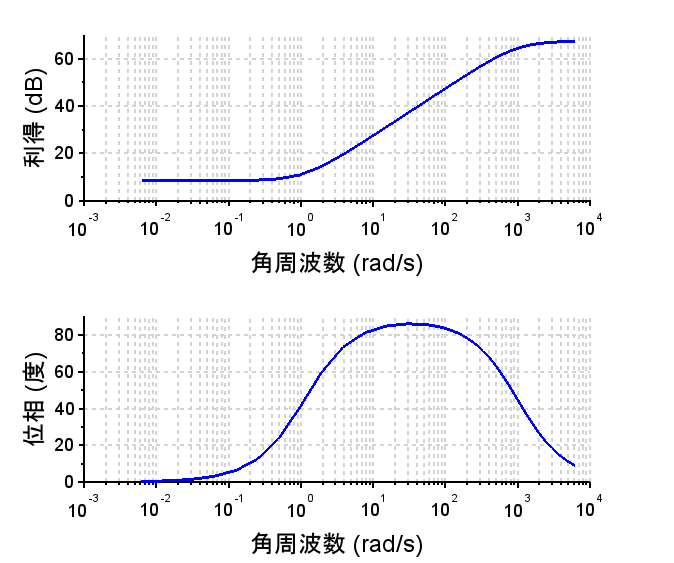
閉ループ伝達関数ボード線図
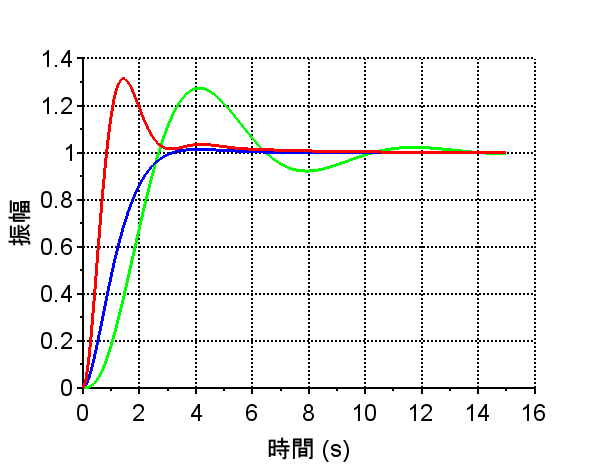
P制御器:緑 PD制御器:青
PID制御器:赤
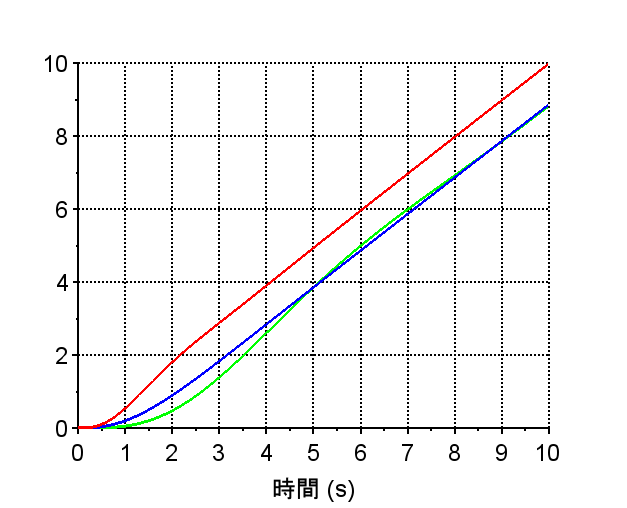
P制御器:緑 PD制御器:青
PID制御器:赤
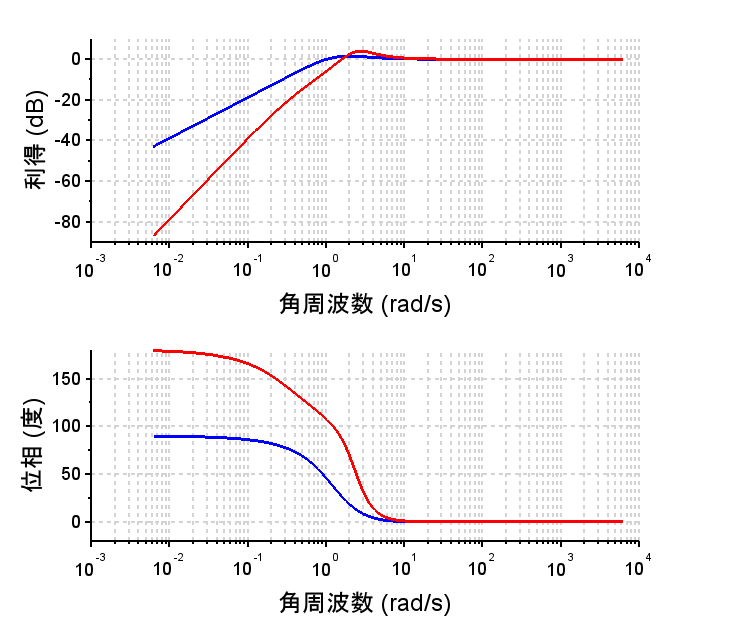
PD制御器:青 PID制御器:赤
PID制御器の使用例
(Scilab スクリプト)
制御対象\(G(s)=\frac{1}{s(s+1)(s+3)}\)とする。
P制御器:P制御器によりゲインを調整した場合、「P制御器のみの開ループ伝達関数ボード線図」から、位相余裕は約42°、利得余裕は約13dBで安定性に問題はないが、ステップ応答(緑線)をみると立ち上がりが遅く、ランプ応答(緑線)では、定常速度偏差が大きい。これは、主には、ゲイン交差周波数が低いこと、低周波数域での利得が低いことに起因する。しかし、ゲインを上げると安定余裕が劣化してしまう。
PD制御器:「PD制御器のボード線図」から分かるように特定周波数以上の位相を進めることが可能となる。Scilabでは、分子の次数が高い伝達関数(非因果的)は扱えないので、高域での利得を抑制するように伝達関数を補正している。(これは、現実的に実装においても妥当である。)「PD制御器を使用した場合のステップ応答(青線)」は立ち上がりも良く、行き過ぎ量も小さい。しかし、ランプ応答(青線)を見ると定常速度偏差が大きい。このPD制御は目標値が大きく変化しない定値制御での使用が妥当と考えられる。
PI制御器:「PI制御器のボード線図」から分かるように特定周波数以下の利得を大きく高めることが可能となる。
PID制御器:「PID制御器のボード線図」を見ると位相進み制御器と位相遅れ制御器を組み合わせた周波数特性に似ている。PID制御器では、設定するパラメータが少ないので、制御システムの状況を観察しながら(\(K_p , K_i , K_d\))の3つのパラメータ調整することができる。ステップ応答(赤線)、ランプ応答(赤線)とも良好で、定常偏差が小さくできている。
感度関数を見ると、PD制御器(青線)に比較して、PID制御器(赤線)では、低周波数域での利得が大きく低下しており、外乱や制御対象の変動に強くなっていることが分かる。
//PID制御器の使用例
clear; clf();
s=%s;
//制御対象
G=1/(s*(s+1)*(s+3));
Gs=syslin('c',G);
//P制御器
K=2.65;
L0=K*G;
L0s=syslin('c',L0);
T0=L0/(1+L0);
T0s=syslin('c',T0);
scf(0);
bode(L0s,'rad');
//PD制御器
PD=2.65*(1+0.89*s)*(1000/(s+1000));
PDs=syslin('c',PD);
scf(1);
bode(PDs,'rad');
L1=PD*G;
T1=L1/(1+L1);
T1s=syslin('c',T1);
//PI制御器
PI=3*(1+1/(3*s));
PIs=syslin('c',PI);
scf(2);
bode(PIs,'rad');
//PID制御器
PID=PI*PD;
PIDs=syslin('c',PID);
scf(3);
bode(PIDs,'rad');
L2=G*PI*PD;
T2=L2/(1+L2);
T2s=syslin('c',T2);
scf(4);
bode(T2s,'rad');
//ステップ応答
t=0:0.1:15;
scf(5);
y0=csim('step',t,T0s);plot2d(t,y0,3); y1=csim('step',t,T1s);plot2d(t,y1,2); y2=csim('step',t,T2s);plot2d(t,y2,5);xgrid;
//ランプ応答
t=0:0.1:10;
scf(6);
y0=csim(t,t,T0s);plot2d(t,y0,3);
y1=csim(t,t,T1s);plot2d(t,y1,2); y2=csim(t,t,T2s);plot2d(t,y2,5);xgrid;
//感度関数の比較
S1=1/(1+L1);
S1s=syslin('c',S1);
S2=1/(1+L2);
S2s=syslin('c',S2);
scf(7);
bode([S1s;S2s],'rad');


“35. PID制御系” に対して2件のコメントがあります。
コメントは受け付けていません。