38. I -PD制御
PID制御器の特長と問題点をまとめて、I-PD制御について説明する。
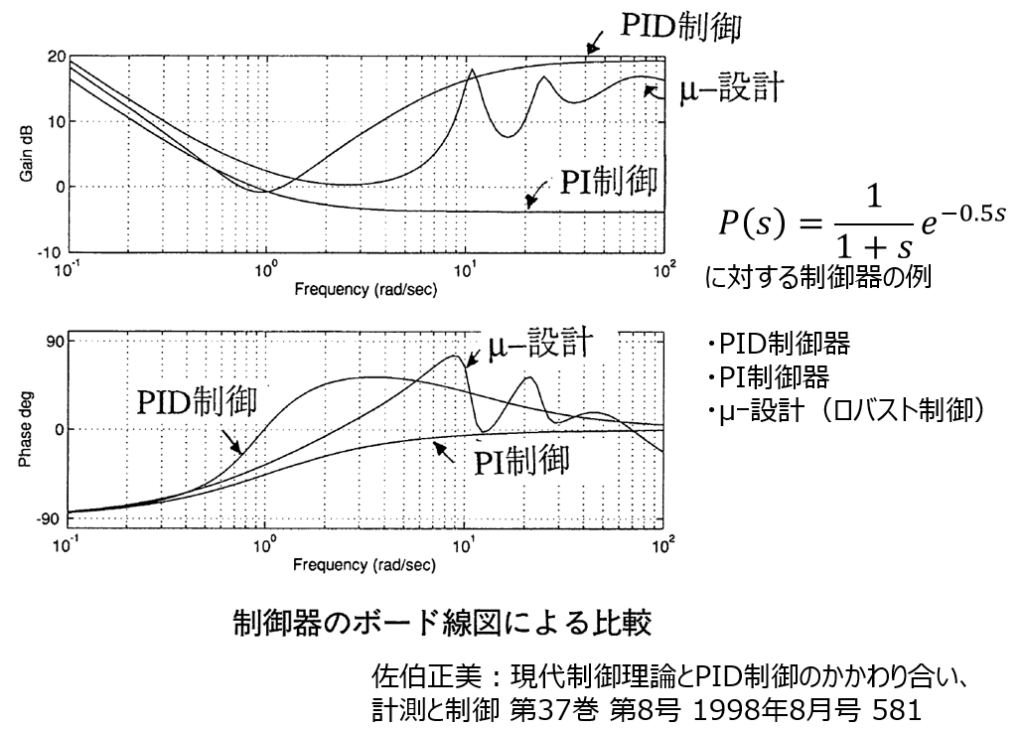
図は、PID制御器、PI制御器、μ-設計(ロバスト制御)を制御対象\(P(s)=\frac{1}{1+s}e^{-0.5s}\)に適用したときの各制御器をボード線図で比較した例である。μ-設計はロバスト制御理論による最適制御器設計である。ボード線図の比較からPID制御器が最適制御器の基本的な特性を実現していることがわかる。μ-設計では、特に高周波数域においてより細かく制御系の調整をしている。
※ロバスト制御理論に関しては、改めて紹介する予定である。
PID制御の目的と特長
PID制御の目的は、制御系を安定にする、定常位置偏差をゼロにする、応答を改善する、感度を低減する、である。
PID制御の特長は、構造が簡単(比例、積分、微分の3要素)で、調整パラメータが少なく調整がしやすい、ことである。
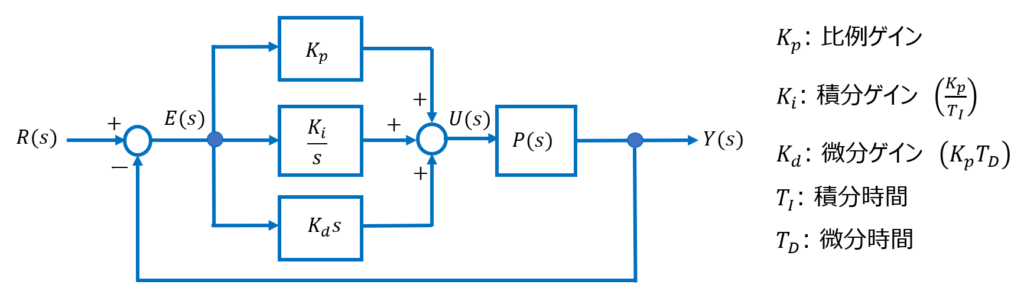
PID制御器の構成
ブロック図「PID制御器の構成」より、$$U(s)=K_p\left\{E(s)+\frac{E(s)K_i}{s}+K_d s E(s)\right\}$$ である。従って、PID制御器の伝達関数は$$C(s)=\frac{U(s)}{E(s)}=K_p + \frac{K_i}{s} + K_d s=K_p\left(1 + \frac{1}{s T_I}+T_D s \right)$$となる。
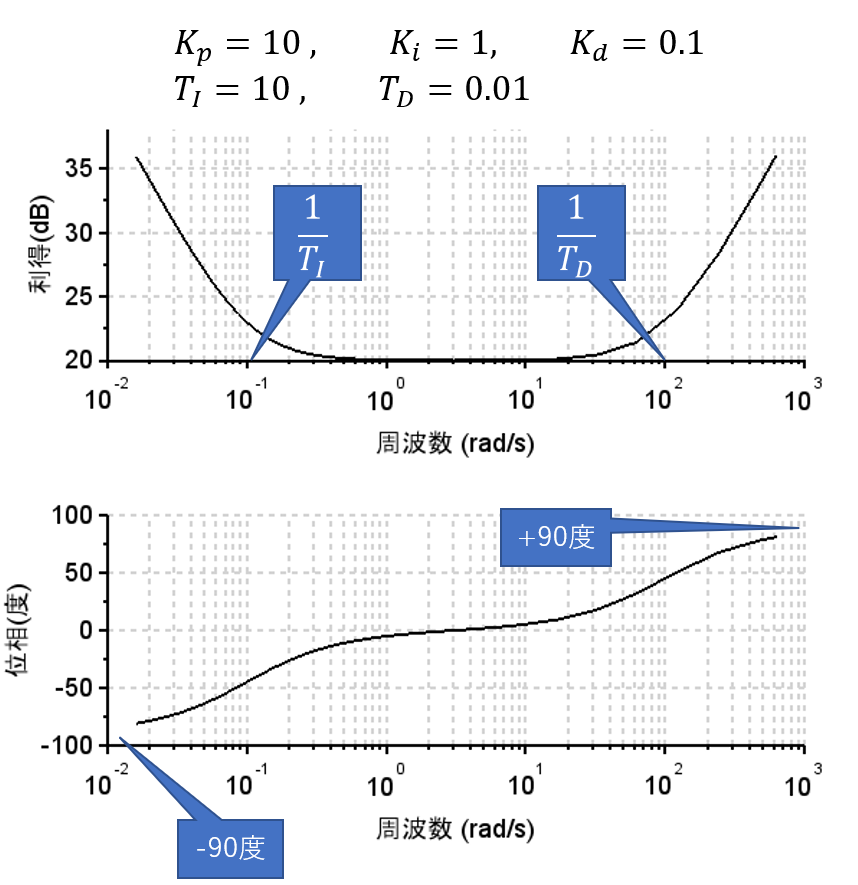
PID制御器の周波数伝達関数は、$$C(j \omega)=K_p \left(1 + \frac{1}{T_I j \omega} +T_D j \omega\right)$$となる。
利得:$$\left|C(j \omega)\right| = \sqrt{K_p^2 +\left(K_p T_D \omega - \frac{K_p}{T_I \omega}\right)^2}$$ 位相:$$\arg\{C(j\omega)\} = \tan^{-1}\left(\frac{K_p T_D \omega - \frac{K_p}{T_I \omega}}{K_p}\right)$$ 「PID制御器のボード線図」を見ると低域と高域の利得が上がり、中域の利得は\(K_p\)の利得となる。また、位相は、\(-90 ^{\text{°}} \sim +90^{\text{°}}\)で変化する。(注:このボード線図は、PID制御器の特徴を明確にするために各パラメータを極端な値にしている。)
PID制御器によるループ整形の例
$$P(s)=\frac{1}{(s+1)(s+2)}$$ を制御対象とする単位フィードバックで、PID制御器により特性改善することを考える。
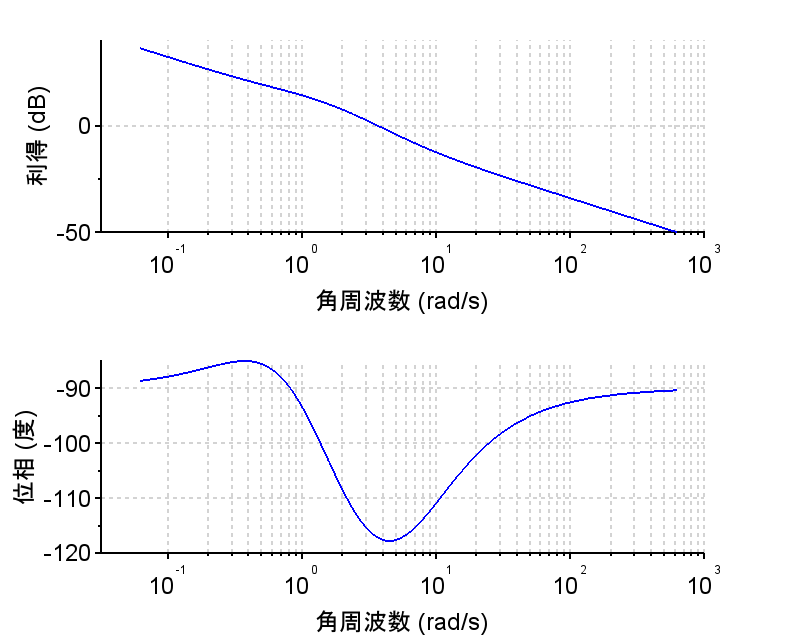
\(K_p=15.0\)、\( K_i=8.0\) 、\(K_d=2.0\) としたとき、I (積分要素)により、低域のゲインが大きくなり、定常位置偏差が\(0\)にできる。また、このときの開ループ伝達関数\(L(s)\)は1型系となっている。
PID制御器の微分キック問題
目標値をステップ状に急変させた場合、PID制御器の微分動作により大きな操作量が発生し、増幅器の飽和などの非線形動作を起こして問題を生じることがある。この微分による急激な動作を微分キックと呼ぶ。
【例】PID制御器の微分キック動作(Xcosによるシミュレーション)
$$P(s)=\frac{1}{1+s}e^{-0.2s}$$ PIDの各パラメータは、\(K_p=3.5\)、\(K_i=3.5\)、\(K_d=0.45\)とする。
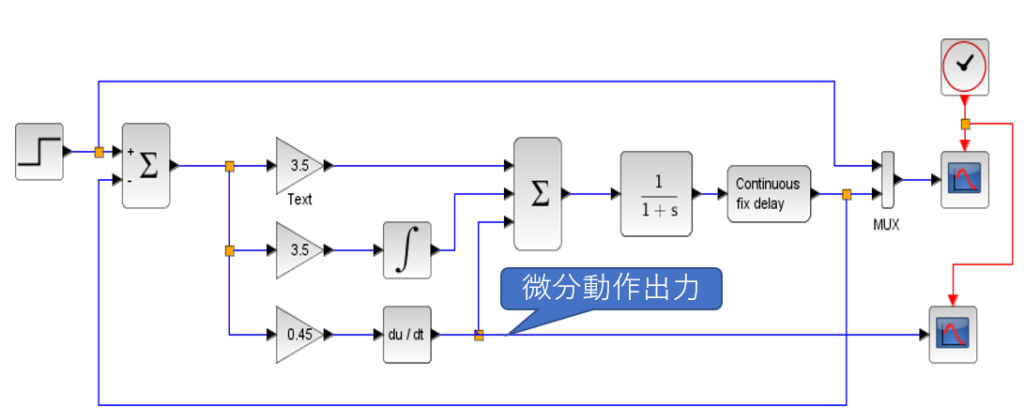
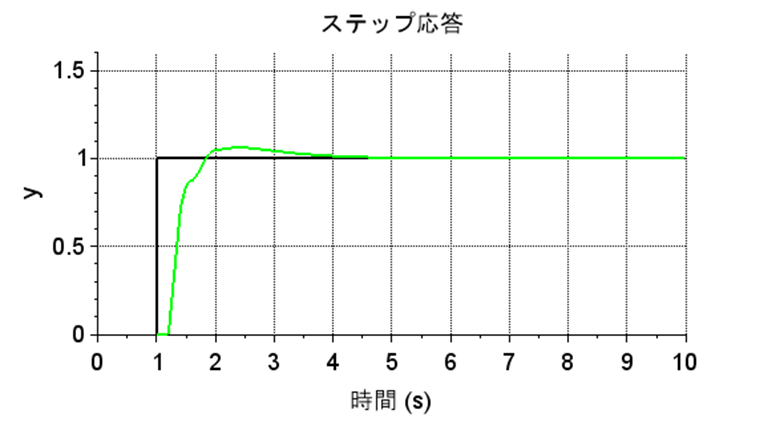
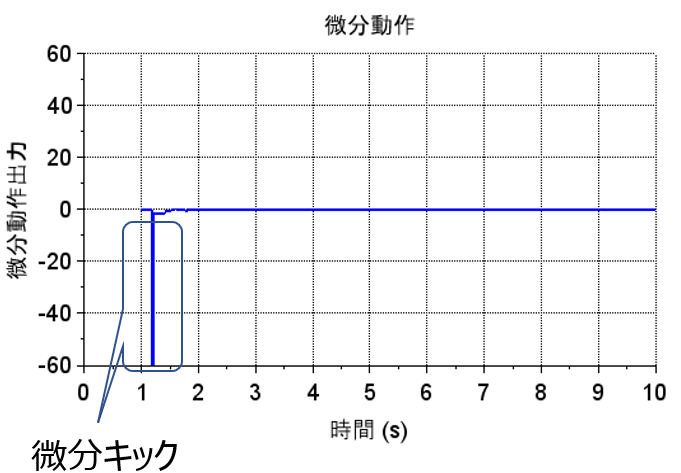
「PID制御器の微分動作」を見ると微分キックが生じており、非線形な動作となっている。シミュレーションでは、微分キックによる増幅器の飽和動作は入れていないが、それでも「PID制御系でのステップ応答」は滑らかでなく、不自然な振動が生じている。実機では、飽和動作の影響によりステップ応答はさらに劣化する。
比例微分先行型PID制御(I-PD制御)の構成
基本的なPID制御器では、目標値が急変した時に微分項、比例項の影響によって操作量が急変する。このため、理論とは異なり、実機では増幅器での操作量の飽和等が起こり、非線形な応答状態が生じる。
これを防止する方式として、比例項と微分項は出力値に対してゲインを掛けフィードバックするというPID制御器の変形である、比例微分先行型PID制御(I-PD制御)がある。
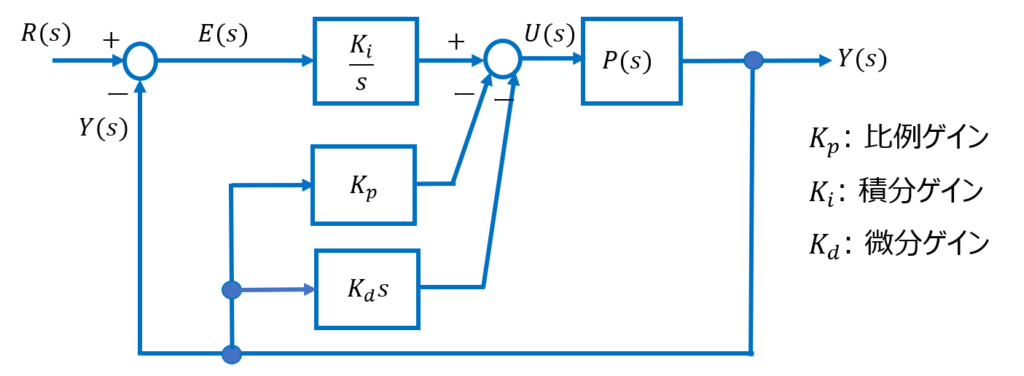
*I-PD制御系の伝達関数
「比例微分先行型PID制御(I-PD制御)系の構成」のブロック図より、
\(E(s)=R(s)-Y(s)\) \(U(s)=\frac{K_i}{s} E(s) - K_p Y(s) - K_d sY(s)\) \(Y(s)=P(s)U(s)\) $$ Y(s)=P(s)\left\{\frac{K_i}{s}\left (R(s) -Y(s)\right) -K_p Y(s)-K_d sY(s)\right\}$$よって、閉ループ伝達関数は、$$T(s)=\frac{Y(s)}{R(s)}=\frac{\left(\frac{K_i}{s}\right)P(s)}{1+P(s)\left(K_p+\frac{K_i}{s}+K_d s\right) }$$となる。この特性方程式は、$$1+P(s)\left(K_p+\frac{K_i}{s}+K_d s\right) =0$$なので、基本PID制御要素により安定化と極配置を決めることができる。
※I-PD制御では出力 \(Y(s)\) を \(K_p\) ,\( K_d s\) でフィードバックする構成となっているため、基本PID制御器の各パラメータは再調整する必要がある。
I-PD制御器の動作
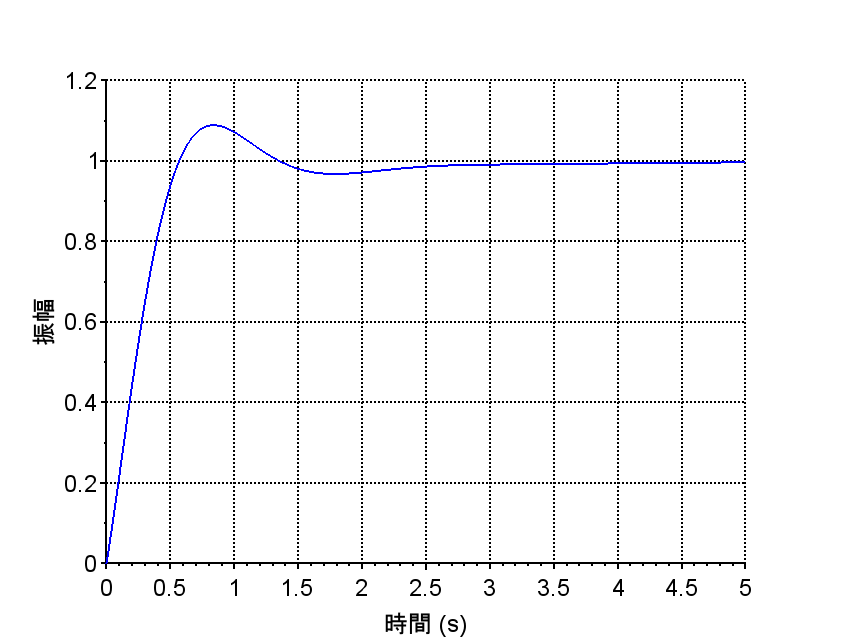
基本PID制御器の微分動作と異なり、微分キックが生じない。ステップ応答は滑らかで、定常位置偏差0が実現できる。
一般にI-PD制御は、一次遅れ系+むだ時間要素となる温度制御や化学反応制御、モータ速度制御系に適している。
【例】 I-PD制御器の微分動作(Xcosによるシミュレーション)
$$P(s)=\frac{1}{1+s}e^{-0.2s}$$ PIDの各パラメータは、\(K_p=3.5\)、\(K_i=8.0\)、\(K_d=0.5\)とする。
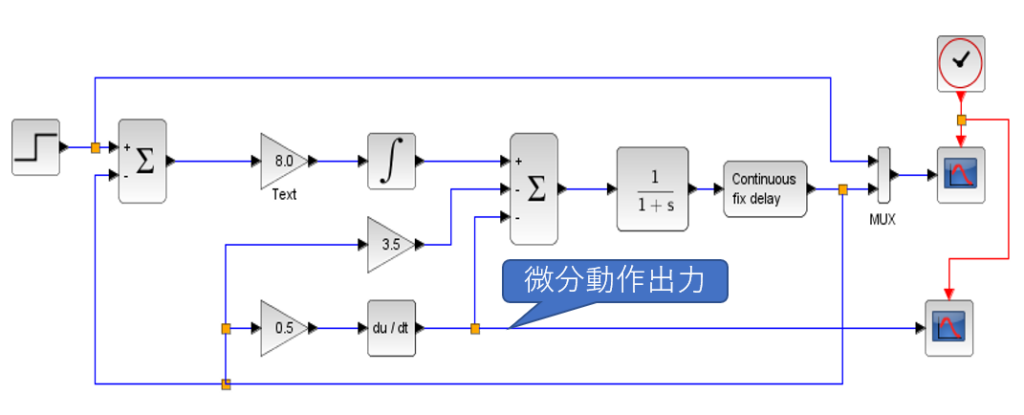
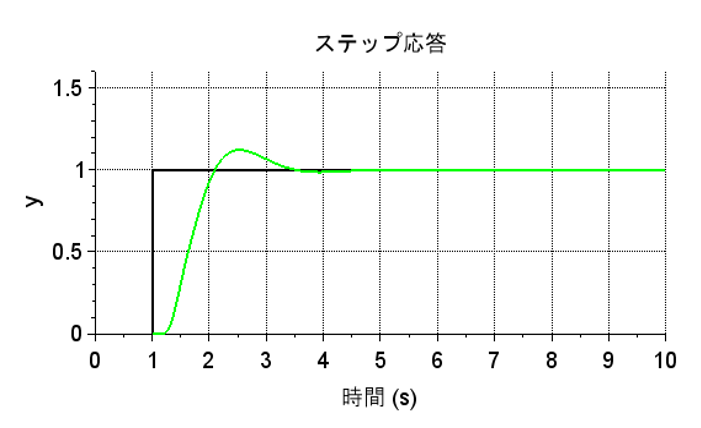
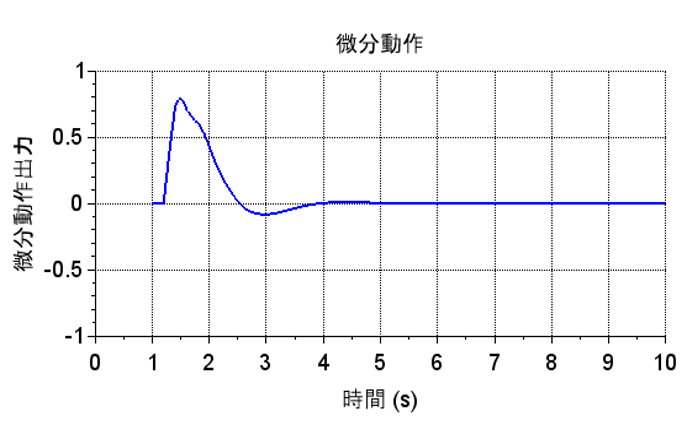
「I-PD制御器の微分動作」より、微分キックが生じず、滑らかな微分動作になっていることが分かる。また、ステップ応答も滑らかであり、定常位置偏差\(0\)が実現できている。

