27. 定常特性と内部モデル原理
定常特性と内部モデル原理について説明する。
ステップ応答と定常偏差
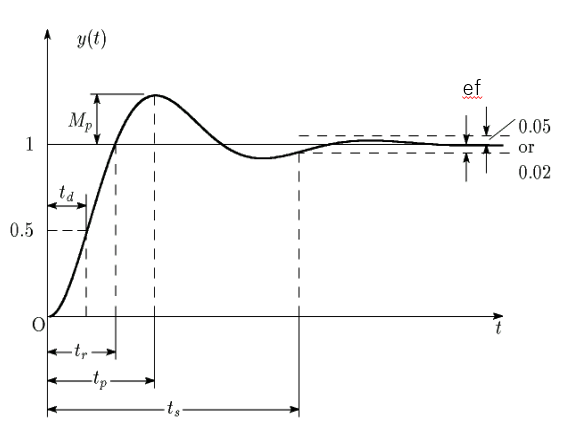
制御の主要な目的は、出力を目標値に近づけることにある。単純には、目標値との差(偏差)をゼロに、出来るだけ速くということになる。 安定な制御系において、定常状態で目標値と出力に偏差がある場合、 これを定常偏差という。
図の単位ステップ応答で考えると、整定時間\(t_s\)後の偏差\(e_f\)が定常偏差である。定常偏差の許容値は、各制御システムの仕様によるが目標値の\(\pm 0.02 \sim \pm 0.05\)程度とすることが多い。勿論、精密機器ではもっと厳しい許容値となる。
目標値の主要な形と偏差
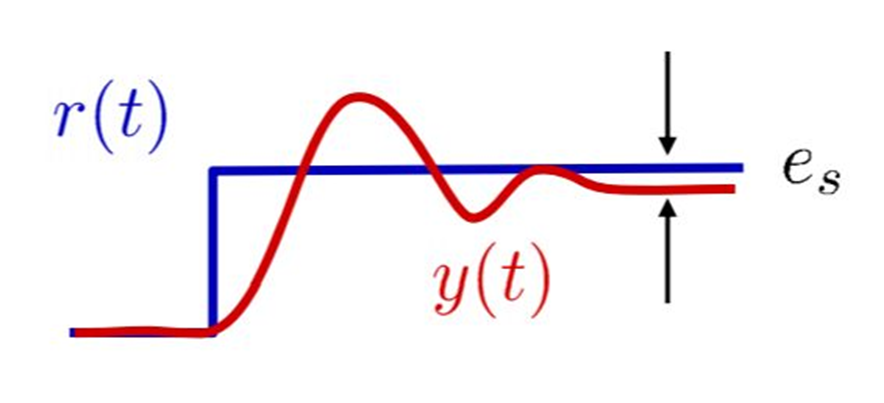
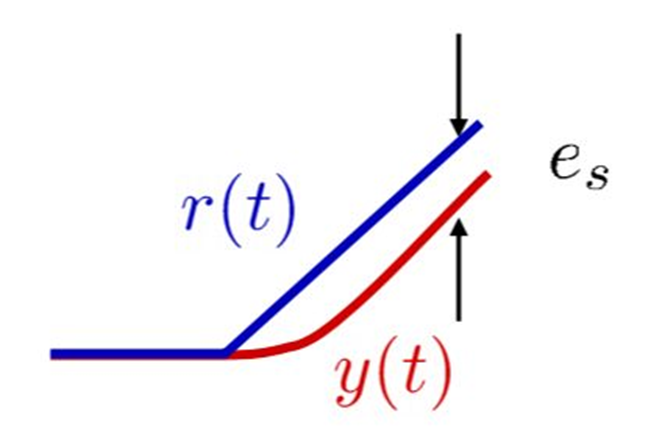
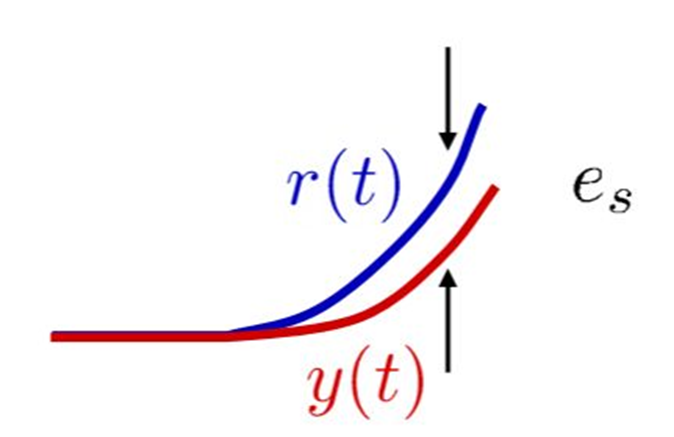
*ステップ信号
ステップ信号を時間関数で表すと、$$r(t)=\begin{cases} 0 \enspace \enspace (t \lt 0) \\ 1 \enspace \enspace (t \geq 0)\end{cases}$$これをラプラス変換すると、$$R(s)=\int_0^\infty r(t)e^{-st}dt$$ $$=\int_0^\infty 1 \cdot e^{-st}dt=\frac{1}{s}$$
*ランプ信号
ランプ信号を時間関数で表すと、$$r(t)=\begin{cases} 0 \enspace \enspace (t \lt 0) \\ t \enspace \enspace (t \geq 0)\end{cases}$$これをラプラス変換すると、$$R(s)=\int_0^\infty r(t)e^{-st}dt$$ $$=\int_0^\infty t \cdot e^{-st}dt=\frac{1}{s^2}$$
*パラボラ信号
ランプ信号を時間関数で表すと、$$r(t)=\begin{cases} 0 \enspace \enspace (t \lt 0) \\ t^2 \enspace \enspace (t \geq 0)\end{cases}$$これをラプラス変換すると、$$R(s)=\int_0^\infty r(t)e^{-st}dt$$ $$=\int_0^\infty t^2 \cdot e^{-st}dt=\frac{2}{s^3}$$
ラプラス変換の最終値定理
ラプラス変換の最終定理は定常偏差を求めるのに使われる。
$$\lim_{t \rightarrow \infty} f(t)=\lim_{s \rightarrow 0}s \cdot F(s)$$
―――――――――――――――――
導関数のラプラス変換より、
$$\int_0^\infty \frac{df(t)}{dt}e^{-st}dt=sF(s)-f(0)$$ $$\lim_{s \rightarrow 0} \int_0^\infty \frac{df(t)}{dt}e^{-st}dt=\lim_{s \rightarrow 0}sF(s)-f(0)$$ $$\int_0^\infty \frac{df(t)}{dt} \cdot 1dt=\lim_{s \rightarrow 0} sF(s)-f(0)$$ $$\int_{f(0)}^{f(\infty)} df(t)=\lim_{s \rightarrow 0}sF(s)-f(0)$$ $$f(\infty)-f(0)=\lim_{s \rightarrow 0}sF(s)-f(0)$$ $$f(\infty)=\lim_{s \rightarrow 0}sF(s)$$
※導関数(微分)のラプラス変換
$$\mathcal{L}\left\{\frac{df(t)}{dt}\right\}=\int_0^\infty \frac{df(t)}{dt}e^{-st}dt$$ $$=\left[f(t)e^{-st}\right]_0^\infty -\int_0^\infty f(t)\left(\frac{d}{dt}e^{-st}\right)dt$$ $$=\left[0 - f(0)\right]-(-s)\int_0^\infty f(t)e^{-st}dt$$ $$=s\mathcal{L} \left\{f(t) \right\}-f(0)$$ $$=sF(s)-f(0)$$
定常偏差
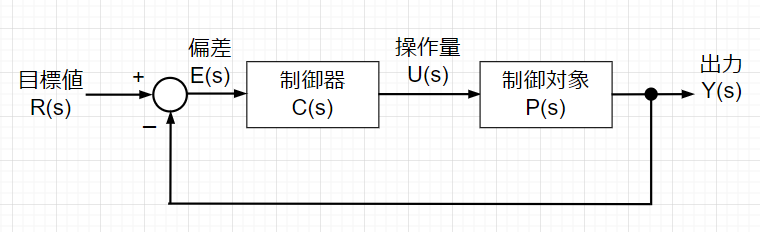
単位フィードバック制御系で考える。
偏差は、\(E(s)=R(s) - Y(s)\)となる。\(Y(s)=C(s)P(s)E(s)\)なので、\(E(s)=R(s) - C(s)P(s)E(s)\) となり、式を整理すると\(\{1+C(s)P(s)\}E(s)=R(s)\) よって、$$E(s)=\frac{1}{1+C(s)P(s)}R(s)$$ \(L(s)=C(s)P(s)\) (\(L(s)\):開ループ伝達関数)として、$$E(s)=\frac{1}{1+L(s)}R(s)$$ となる。$$S(s)=\frac{E(s)}{R(s)}=\frac{1}{1+L(s)}$$を感度関数という。感度関数\(S(s)\)は、目標値から偏差までの伝達関数である。偏差はs領域で\(E(s)=\frac{1}{1+L(s)}R(s)\)なので、十分に時間が経った時の偏差は、最終値定理より、$$e_s=\lim_{t \rightarrow \infty} e(t)=\lim_{s \rightarrow 0} s\cdot E(s)$$で求まる。
目標値がステップ信号の場合の定常偏差(定常位置偏差)
目標値がステップ信号の場合の定常偏差、定常位置偏差\(e_p\)は、ステップ信号\(r(t)\)のラプラス変換が\(R(s)=\frac{1}{s}\)なので、$$e_p=\lim_{s \rightarrow 0} s \cdot E(s)=\lim_{s \rightarrow 0}s \cdot \frac{1}{1+L(s)} \cdot R(s)$$ $$=\lim_{s \rightarrow 0}s \cdot \frac{1}{1+L(s)} \cdot \frac{1}{s}=\frac{1}{1+L(0)}=\frac{1}{1+K_p}$$となる。ここで、$$K_p=\lim_{s \rightarrow 0}L(s)=L(0)$$を位置偏差定数という。
※\(K_p\) すなわち\(L(0)\)の利得、すなわち 開ループのDCゲインを大きくすると定常位置偏差は小さくできることになる。
目標値がランプ信号の場合の定常偏差(定常速度偏差)
目標値がランプ信号の場合の定常偏差、定常速度偏差\(e_v\)は、ランプ信号\(r(t)\)のラプラス変換が\(R(s)=\frac{1}{s^2}\)なので、$$e_v=\lim_{s \rightarrow 0} s \cdot E(s)=\lim_{s \rightarrow 0}s \cdot \frac{1}{1+L(s)} \cdot R(s)$$ $$=\lim_{s \rightarrow 0}s \cdot \frac{1}{1+L(s)} \cdot \frac{1}{s^2}=\lim_{s \rightarrow 0} \frac{1}{s+sL(s)}$$ $$=\lim_{s \rightarrow 0}\frac{1}{sL(s)}=\frac{1}{K_v}$$となる。ここで、$$K_v=\lim_{s \rightarrow 0} sL(s)$$を速度偏差定数という。
目標値がパラボラ信号の場合の定常偏差(定常加速度偏差)
目標値がパラボラ信号の場合の定常偏差、定常加速度偏差\(e_a\)は、パラボラ信号\(r(t)\)のラプラス変換が\(R(s)=\frac{2}{s^3}\)なので、$$e_a=\lim_{s \rightarrow 0} s \cdot E(s)=\lim_{s \rightarrow 0}s \cdot \frac{1}{1+L(s)} \cdot R(s)$$ $$=\lim_{s \rightarrow 0}s \cdot \frac{1}{1+L(s)} \cdot \frac{2}{s^3}=\lim_{s \rightarrow 0} \frac{2}{s^2+s^2L(s)}$$ $$=\lim_{s \rightarrow 0}\frac{2}{s^2 L(s)}=\frac{2}{K_a}$$となる。ここで、$$K_a=\lim_{s \rightarrow 0} s^2 L(s)$$を加速度偏差定数という。
定常偏差を0にするには(内部モデル原理)
目標値に対する偏差は、$$E(s)=S(s)R(s)=\frac{1}{1+L(s) } R(s)$$である。
*目標値がステップ信号の場合の定常偏差(定常位置偏差)は、$$e_p=\frac{1}{1+L(0)}=\frac{1}{1+K_p}$$なので、$$K_p=\lim_{s \rightarrow 0}L(s)=L(0)$$において、\(K_p \rightarrow \infty\)で定常位置偏差\(e_p\)は\(0\)になる。これを実現するには、\(L(s)\)に\(\frac{1}{s}\)(積分要素)が含まれているとよいことになる。
*目標値がランプ信号の場合の定常偏差(定常速度偏差)は、$$e_v=\frac{1}{s+sL(s)}=\frac{1}{sL(s)}=\frac{1}{K_v}$$なので、$$K_v=\lim_{s \rightarrow 0}sL(s)$$において、\(K_v \rightarrow \infty\)で定常速度偏差\(e_v\)は\(0\)になる。これを実現するには、\(L(s)\)に\(\frac{1}{s^2}\)(2重積分要素)が含まれているとよいことになる。
*目標値がパラボラ信号の場合の定常偏差(定常加速度偏差)は、$$e_a=\frac{2}{s^2+s^2L(s)}=\frac{2}{s^2L(s)}=\frac{2}{K_a}$$なので、$$K_a=\lim_{s \rightarrow 0}s^2 L(s)$$において、\(K_a \rightarrow \infty\)で定常加速度偏差\(e_a\)は\(0\)になる。これを実現するには、\(L(s)\)に\(\frac{1}{s^3}\)(3重積分要素)が含まれているとよいことになる。
内部モデル原理
内部モデル原理とは、「開ループ伝達関数\(L(s)\)が追従したい目標値信号のモデルを含んでいるとき、定常偏差を0にできる。」というものである。開ループ伝達関数\(L(s)\)が積分要素\(\frac{1}{s}\)を1つ含んでいるとき1型、2つ含んでいるとき2型という。従って、目標値信号がステップ信号(\(\frac{1}{s}\))のとき、\(L(s)\)が1型であれば、定常偏差を0にできることになる。



“27. 定常特性と内部モデル原理” に対して6件のコメントがあります。
コメントは受け付けていません。