9. 対角正準形

正準形式とは、数学的な問題やモデルを、標準的な形に変換することを指す。正準形式は、数学的に扱いやすい形に変換することで、問題の性質を明確にし、解法を簡単化することができる。

対角正準形は、状態方程式を対角行列の形に変換することで、システムの特性を明確にする方法の1つである。状態方程式を対角正準形に変換することで、システムの固有値が明確になる。変換後の行列 の非対角要素は、システムの状態変数同士の相互作用を表すため、対角正準形に変換することで、システムの状態変数同士の影響度合いも明確になる。また、対角正準形は、システムの安定性や応答特性の解析に役立ち、対角正準形に変換することで、システムの制御設計が容易になる。

１入力１出力システムの対角正準形

適当な状態変換行列\(\boldsymbol{T}\)を設定して、\(\boldsymbol{\tilde{A} , \;\tilde{B} ,\;\tilde{C}}\)のどれかが使い易い形式にできたとき、それらを正準形式といい、それにより構成されたシステムを正準システムという。

\(\boldsymbol{A}\)が重複した固有値を持たないとき、固有値を\(\lambda_1 \sim \lambda_n\)、固有ベクトルを\(\boldsymbol{v}_1 \sim \boldsymbol{v}_n\)とする。このとき、$$\boldsymbol{T} = [\boldsymbol{v}_1,\boldsymbol{v}_2, \cdots , \boldsymbol{v}_n]$$の対角変換行列によって、\(\boldsymbol{x}(t) = \boldsymbol{Tz}(t)\)の変換をすると、\(\boldsymbol{\tilde{A}}\)が対角正準形式（対角が固有値の対角行列）となる。$$\boldsymbol{\tilde{A}} = \boldsymbol{\Lambda} = \boldsymbol{T}^{-1} \boldsymbol{AT} = \begin{bmatrix} \lambda_1 & & \boldsymbol{0} & \\ & \lambda_2 & & \\ & & \ddots & \\ & \boldsymbol{0} & & \lambda_n \end{bmatrix}$$また、$$\boldsymbol{\tilde{b}}=\begin{bmatrix} \tilde{b}_1 \\ \tilde{b}_2 \\ \vdots \\ \tilde{b}_n \end{bmatrix} , \;\;\;\; \boldsymbol{\tilde{c}} = \begin{bmatrix} \tilde{c}_1 & \tilde{c}_2 & \cdots &\tilde{c}_n \end{bmatrix}$$とすると、対角正準システム　$$\begin{bmatrix} \dot{z}_1 \\ \dot{z}_2 \\ \vdots \\ \dot{z}_n \end{bmatrix} = \begin{bmatrix} \lambda_1 & & \boldsymbol{0} & \\ & \lambda_2 & & \\ & & \ddots & \\ & \boldsymbol{0} & & \lambda_n \end{bmatrix} \begin{bmatrix} z_1 \\ z_2 \\ \vdots \\ z_n \end{bmatrix} + \begin{bmatrix} \tilde{b}_1 \\ \tilde{b}_2 \\ \vdots \\ \tilde{b}_n \end{bmatrix} u $$　$$ y = \begin{bmatrix} \tilde{c}_1 & \tilde{c}_2 & \cdots &\tilde{c}_n \end{bmatrix} \begin{bmatrix} z_1 \\ z_2 \\ \vdots \\ z_n \end{bmatrix} $$が得られる。これを状態変数線図で表すと、図「対角正準システム」となる。

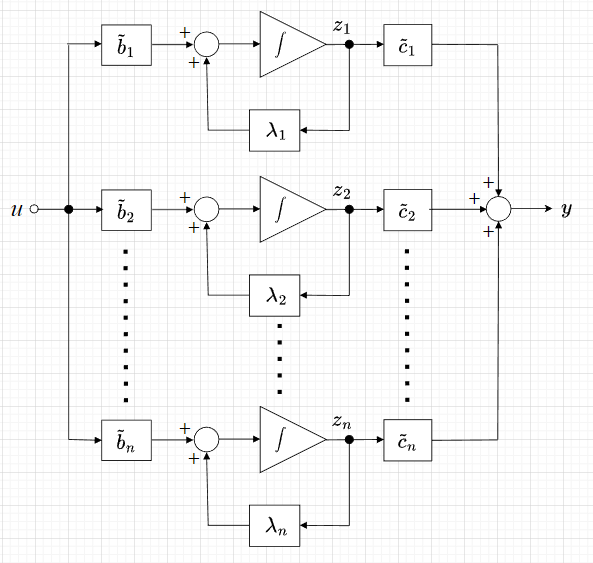
図「対角正準システム」から分かるように、入力が１つで、内部は\(n\)個の並列システムで構成され、出力はその和となっている。すなわち、$$ \dot{z}_i =\lambda_i z_i + \tilde{b}_i u \;\;\; (i = 1 \sim n) \\ y = \tilde{c}_1 z_1 + \tilde{c}_2 z_2 + \cdots + \tilde{c}_n z_n $$である。 この式をラプラス変換し、入出力の比をとると伝達関数が求まる。$$G(s) = \frac{Y(s)}{U(s)}=\boldsymbol{\tilde{c}}(s\boldsymbol{I} - \boldsymbol{\tilde{A}})^{-1} \boldsymbol{\tilde{b}} = \sum_{i=1}^{n} \frac{\tilde{c}_i \tilde{b}_i}{s - \lambda_i}$$ここで、\(\tilde{c}_i \tilde{b}_i\)は、\(s =\lambda_i\)における\(G(s)\)についての留数（伝達関数\(G(s)\)を部分分数展開したときの分子の係数）となっている。つまり、
$$G(s) = \sum_{i=1}^{n} \frac{\tilde{c}_i \tilde{b}_i}{s - \lambda_i} = \frac{\tilde{c}_1 \tilde{b}_1}{s - \lambda_1} + \frac{\tilde{c}_2\tilde{b}_2}{s - \lambda_2} + \cdots + \frac{\tilde{c}_n \tilde{b}_n}{s - \lambda_n}$$なので、これを逆ラプラス変換するとインパルス応答が求まり、$$g(t) = \tilde{c}_1 \tilde{b}_1 e^{\lambda_1 t} + \tilde{c}_2 \tilde{b}_2 e^{\lambda_2 t} + \cdots + \tilde{c}_n \tilde{b}_n e^{\lambda_n t} $$となる。 これより、全ての極\(\lambda_i\)（\(\boldsymbol{A}\)の固有値）の実部が負（\(Re\{\lambda_i\} \lt 0\)）であれば、インパルス応答は、$$\lim_{t \rightarrow \infty} g(t) \rightarrow 0$$なので、安定なシステムとなることが分かる。
また、\(z_i(t)\)をモードと言い、モード解析に利用される。例えば、\(u(t)=0\)とすると、$$z_i(t) = e^{\lambda_i t}z_i (0) \;\;\;\;\; (i = 1 \sim n )$$となる。これを\(\boldsymbol{x}(t) = \boldsymbol{Tz}(t)\)に代入して、$$\boldsymbol{x}(t) = \boldsymbol{v}_1 e^{\lambda_1 t}z_1 (0) + \boldsymbol{v}_2 e^{\lambda_2 t}z_2 (0) + \cdots +\boldsymbol{v}_n e^{\lambda_n t}z_n (0)$$が得られる。これを、状態変数の応答のモード展開という。極\(\lambda_i\)が複素平面の左半平面にあれば、システムは安定であり、極\(\lambda_i\)が虚軸より遠いほどモードは速く\(0\)に収束する。
また、ある程度時間が経つと、\(\boldsymbol{x}(t)\)は、虚軸に最も近い極をもつモードの成分に近似できる。このモードを代表モードといい、代表モードの極\(\lambda_i\)を代表極という。