12. 交流の測定原理
交流とは
交流とは、時間の経過とともに周期的に大きさや向きが変化する電流や電圧を指す。
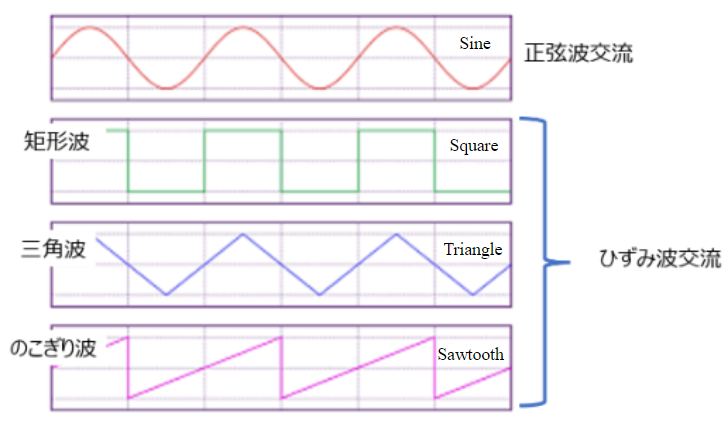
交流を扱う場合、通常、正弦波交流を基準として考える。矩形波、三角波、のこぎり波などは、ひずみ波交流という。
交流の電流・電圧を測定する場合、その実効値を測定する。
交流と脈流
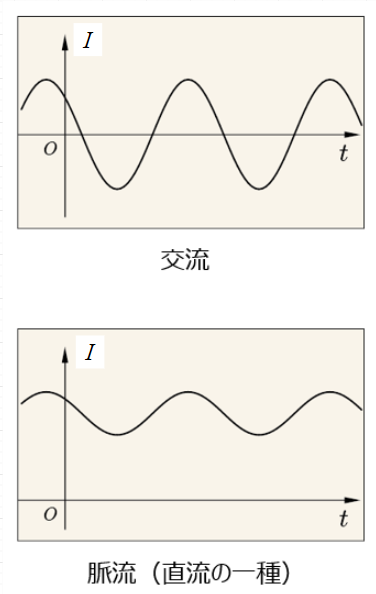
交流は、電流・電圧が正負の極性を繰り返す波形をもつ。
脈流は、電流・電圧の方向が一定で、大きさが周期的、又は不定期な変動を伴った波形をもつ。
従って、脈流は変動を伴う直流と考えることもできる。
実効値
交流電圧や電流の実効値とは、その電圧や電流の振幅が時間的に変化する場合に、その電圧や電流が等価的な直流電圧や直流電流として表したときの値を指す。つまり、直流で発生する電力と同じ電力を発生する交流の電圧、電流を実効値とする。
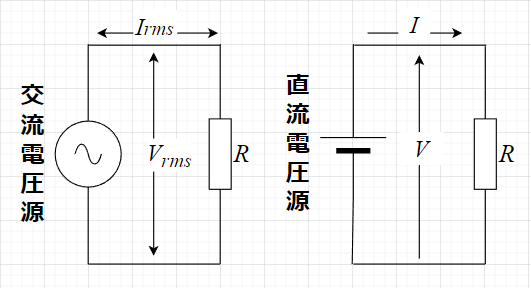
図「実効値」で、$$P=\frac{V_{rms}^2}{R} = \frac{V^2}{R} \; [W]$$あるいは、$$P=I_{rms}^2 R = I^2 R \;[W]$$のとき、\(V_{rms} \;\; I_{rms}\)を実効値という。
正弦波電圧のp-p値、平均値
正弦波電圧を$$v(t) = V_m \sin(\omega t)$$とする。ここで、
\(V_m\):振幅[V]
\(\omega = 2\pi f\):角周波数 [rad/s]
\(T\):周期 [s] 、 \(f=1/T\):周波数 [Hz]
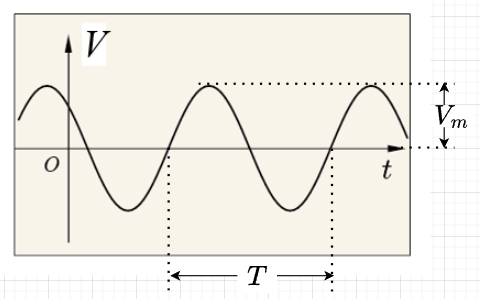
p-p値(peak to peak Voltage):\(V_{pp}\)は、波形の最大値と最小値の差を表している。正弦波の場合、\(V_{pp}\)は振幅の2倍になる。\(V_{pp} = 2V_m\)
平均値:\(V_{ave} = \frac{2}{\pi}V_m \) 一周期で平均をとると正の半波と負の半波で打ち消すので0となる。その為、平均は絶対値\(|v(t)|\)で求める。従って、半周期の平均を計算すればよい。$$V_{ave} = \frac{2}{T} \int_0^{\frac{T}{2}} V_m \sin\omega t dt = -\frac{2V_m}{T \omega}\left[\cos \omega t\right]_0^{\frac{T}{2}} \\ = -\frac{2V_m}{T \omega} \left[\cos \omega \frac{T}{2} - \cos 0\right] \\ = \frac{2}{\pi} V_m $$
正弦波電圧の実効値
実効値は、交流電力が直流電力と等しくなる時の、交流の電流値や電圧値である。従って、平均電力が等しくなる直流に換算した値で、電力は電圧や電流の2乗に比例するから、実効値を求めるには、2乗し平均をとり、その平方根を計算すればよい。
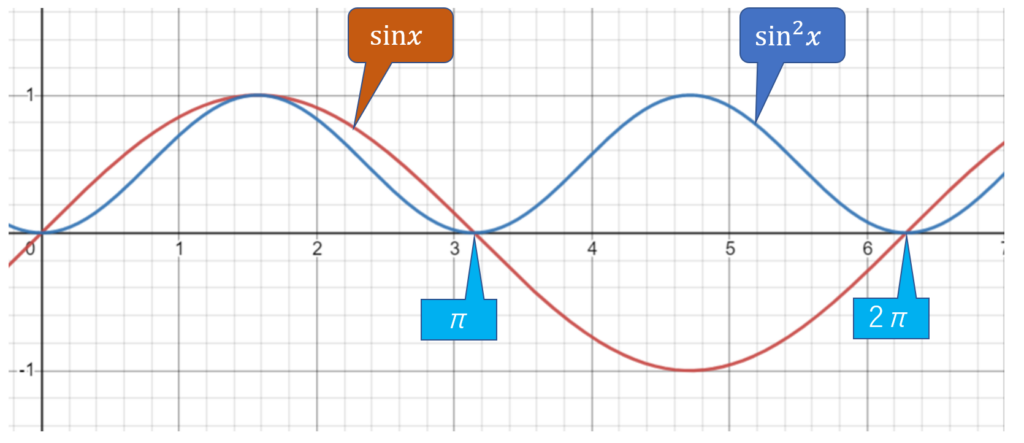
まず、正弦波電圧の2乗の一周期の積分値を求める。$$X=\int_0^{T}(V_m \sin \omega t)^2dt = {V_m}^2 \int_0^T (\sin \omega t)^2 dt \\= {V_m}^2 \int_0^T \frac{1 - \cos 2 \omega t}{2} dt = {V_m}^2 \left[\frac{1}{2}t - \frac{1}{4 \omega} \sin 2 \omega t \right]_0^T \\= \frac{{V_m}^2T}{2}$$ よって、実効値は $$V_{rms} =\sqrt{\frac{X}{T}} = \frac{V_m}{\sqrt{2}}$$この実効値は、正弦波電圧の場合であることに注意。
※家庭用電源の100Vは実効値を示している。従って、振幅\(V_m\)は\(100 \times \sqrt{2} =141.4 V\)である。
交流の実効値
交流電圧、交流電圧の実効値は、波形に関わらず以下の式で求める。
交流電圧の実効値:$$V_{rms} = \sqrt{\frac{1}{T} \int_0^T v(t)^2 dt} \;\;[V]$$交流電流の実効値:$$I_{rms} = \sqrt{\frac{1}{T} \int_0^T i(t)^2 dt} \;\;[A]$$
交流の実効値測定 可動鉄片形計器
実効値電圧:\(V\; \)[V] , 初期位相角:\(\alpha \; \)[rad]
実効値電流:\(I \; \) [A] , 初期位相角:\(\beta \; \)[rad]
角周波数:\(\omega = 2 \pi f\)[rad/s]
正弦波電圧:\(v(t) = V_m \sin(\omega t + \alpha) \)[V]
(\(V_m = \sqrt{2} V\))
正弦波電流:\(i(t) = I_m \sin( \omega t+ \beta) \)[A]
(\(I_m = \sqrt{2}I\))
とする。
可動鉄片形計器では、測定電流が流れる固定コイルの中に置かれた固定鉄片と可動鉄片に働く電磁反発力を駆動トルクとして指針を動かす。図「可動鉄片形計器の構造」において、測定電流は交流なので、電流が逆方向になると各鉄片の磁化方向も逆になる(両方ともN、Sが入れ替わる)ので、結局、固定鉄片と可動鉄片に働く電磁力は反発力となる。
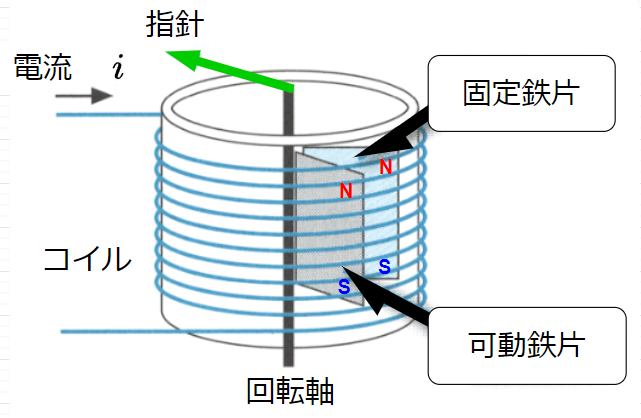
図「可動鉄片形計器の構造」において、二つの鉄片の個々において磁極の強さは電流に比例し、発生する力は電流の2乗に比例する。従って、指針の偏位\(\theta\)は$$\theta \propto F \propto (I_m \sin \omega t)^2 = {I_m}^2 \left(\frac{1 - \cos 2 \omega t}{2} \right)= \frac{{I_m}^2}{2} - \frac{{I_m}^2 \cos 2\omega t}{2} = I^2 - I^2 \cos 2 \omega t$$第1項が実効値に直接関係する量(指針の偏位\(\theta\)は、実効値の2乗に比例)
第2項は振動項だが商用周波数(西日本60Hz、東日本50Hz)程度以上では大きく減衰し、指針の指示値には現れない。
永久磁石可動コイル形計器を利用した交流の測定:整流形
投稿済みの直流の測定原理にあるように、永久磁石可動コイル形計器は直流測定ができる。そこで、交流を整流して直流に変換することで、永久磁石可動コイル形計器を交流の測定に使えるようにする。
図「ブリッジ形全波整流回路と電流の流れ」から、交流電源からの交流電流(赤線、青線)はブリッジ形全波整流回路を通ることにより、計器に流れる電流は一方向となる。これにより、計器として直流用の永久磁石可動コイル形計器が使えることになる。
(ブリッジ形全波整流回路に使われる素子は、4個のダイオードであるが、ブリッジダイオードとして1パッケージになっている製品もある。)
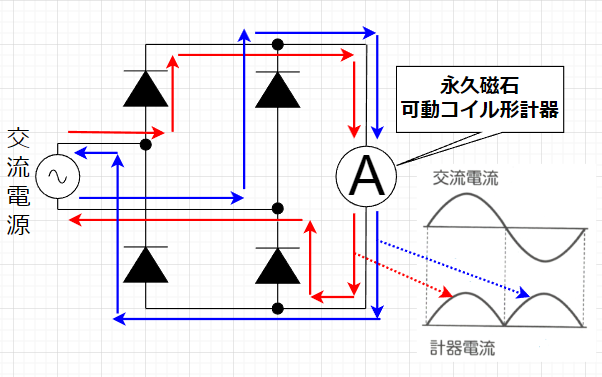
整流器を通って直流に変換された電流で、永久磁石可動コイル形計器を作動させることになるが、このときの波形は平均値を指すことになる。$$V_a = \frac{1}{T} \int_0^T |\sqrt{2}V \sin \omega t |dt =\frac{2\sqrt{2} V}{T} \int_0^{\frac{T}{2}} \sin \omega t dt \\ = \frac{2 \sqrt{2} V}{T} \left[ \frac{ - \cos \omega t}{\omega}\right ]_0^{\frac{T}{2}} \\ = \frac{2 \sqrt{2} V}{\pi} \approx 0.9003V \; [V]$$ この平均値\(V_a\)は実効値と比例の関係になっているので計器の目盛で補正すればよい。
高周波電流の測定:熱電形
可動鉄片形計器は、数百Hz程度までの周波数限界がある。熱電形電流計では、熱線に測定しようとする電流を流し、その発生ジュール熱に比例する温度上昇を熱電対によって熱起電力に変換し、これを可動コイル形指示計器で測定する。このため、直流から数十MHzまでと測定周波数範囲が広く、また、波形に依存しない。
熱電対は、2種類の金属を環状に接続し、一方の接続点と他方に温度差を与えると、温度差に比例した電流が流れることを利用したもの(熱電効果)。この電流計では、熱線で熱電対の片方の接続点を加熱する。
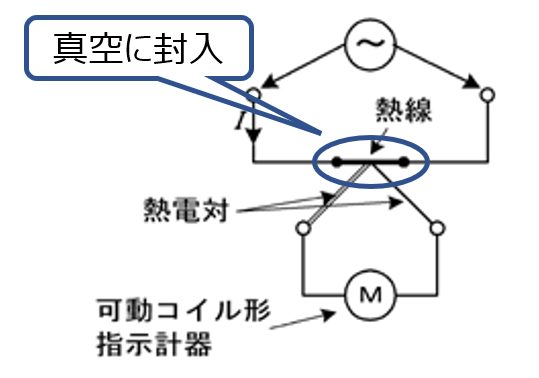
熱線に電流を流すと、その温度上昇は熱線で発生する熱量(=電力\(P\))に比例するが、電力\(P\)は(計測する)電流\(I\)の2乗に比例する。 一方、熱電対に起こる熱起電力(=熱電流\(I\)=電流計Mの振れ)は温度上昇に比例するため、結果として、Mの振れは計測対象\(I^2\)に比例する。つまり、熱電対形電流計は2乗目盛となる。


“12. 交流の測定原理” に対して1件のコメントがあります。
コメントは受け付けていません。