25. 代表極(代表根)と応答特性
制御系の主な応答特性(インパルス応答、ステップ応答、周波数特性など)を決めるのは代表極(代表根)である。代表極に関して例を見ながら説明する。
制御系の極とインパルス応答
代表的な制御対象は1次遅れ要素や2次遅れ要素であるが、それ以上の高次の制御対象はどのように考えれば良いだろうか。まず、制御対象の伝達関数における極とインパルス応答の関係から、主要な特性を決める代表極(代表根)について考える。
極が実数の場合のインパルス応答
【例】\(G(s)=\frac{K}{s+a}\)で与えられる伝達関数(1次遅れ要素)を考える。
極は特性方程式\(s+a=0\)より、\(-a\) である。また、インパルス応答は、$$g(t)=\mathcal{L}^{-1}\left\{G(s)\right\}=Ke^{-at}$$となる。従って、
*\(a \gt 0\)のとき、十分に時間が経ったインパルス応答は\(g(\infty)=0\)となり、この制御系は安定である。極は複素平面の左半平面にあり\(|a|\)が大きいほど速く収束する。
*\(a=0\)のとき、\(g(t)=K\)となり、安定限界である。
*\(a \lt 0\)のとき、インパルス応答は時間の経過とともに\(g(\infty)=\infty\)となり、制御系は不安定となる。極は複素平面の右半平面にあり\(|a|\)が大きいほど速く発散する。
※極が複素平面の左半平面にあり虚軸に近いほど、長い時間、インパルス応答が0に収束しないことになる。つまり、ゆっくりとした時間応答特性になる。逆に虚軸から遠い極であれば、インパルス応答は速く0に収束する。つまり、速い時間応答、素早い動作となる。
極が複素数の場合のインパルス応答
【例】\(G(s)=\frac{\omega}{s^2 + 2as + a^2 + \omega^2}\)の制御対象(2次遅れ要素)を考える。(\(a , \omega\)は実数とする。)
特性方程式\(s^2 + 2as + a^2 + \omega^2=0\)より、特性根は\(s=-a \pm \sqrt{a^2-(a^2 + \omega^2)} =-a \pm j\omega\)となる。従って、極は\(-a \pm j\omega\)である。
$$G(s)=\frac{\omega}{s^2 + 2as + a^2 + \omega^2}$$ $$=\frac{\omega}{(s + a)^2 + \omega^2} $$ なので、インパルス応答は、$$g(t)=\mathcal{L}^{-1}\left\{G(s)\right\}=e^{-at}\sin \omega t $$となる。
*\(a \gt 0\)のとき、インパルス応答は減衰振動となる。十分に時間が経ったインパルス応答は\(g(\infty)=0\)なので、制御系は安定である。極は複素平面の左半平面にあり\(|a|\)が大きいほど速く収束する。また、\(\omega\)が大きいほど 速い振動で0に収束する。
*\(a=0\)のとき、\(g(t)=\sin \omega t\)となり、インパルス応答は定常振動となる。これは安定限界である。また、\(\omega\)が大きいほど 速い振動となる。
*\(a \lt 0\)のとき、インパルス応答は発散振動となる。インパルス応答は時間の経過とともに\(g(\infty)=\infty\)となり、制御系は不安定である。極は複素平面の右半平面にあり\(|a|\)が大きいほど速く発散する。また、\(\omega\)が大きいほど 速い振動で発散する。
代表極による特性の違い
代表極(代表根)の複素平面上の位置による特性(時間応答特性、周波数特性)の違いを具体例で見る。代表極は制御系の応答特性に影響を与える時間が長い極であり、それは虚軸に近い極である。
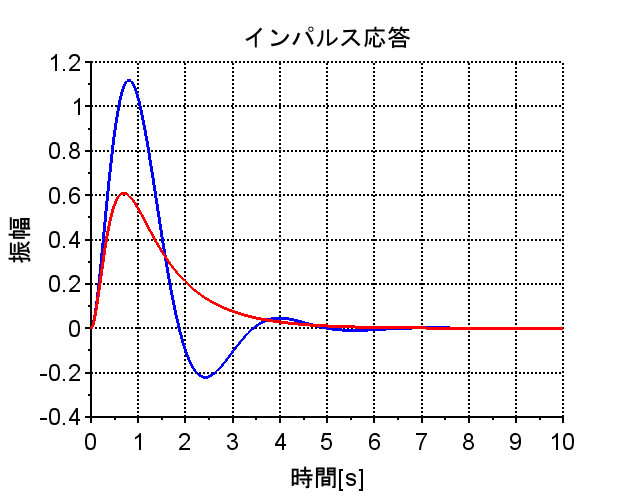
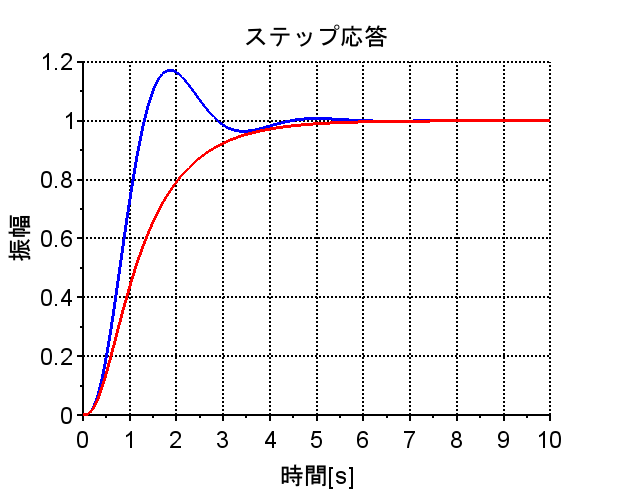
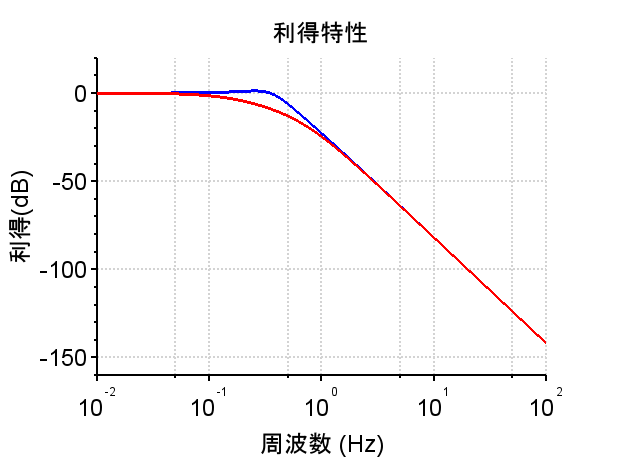
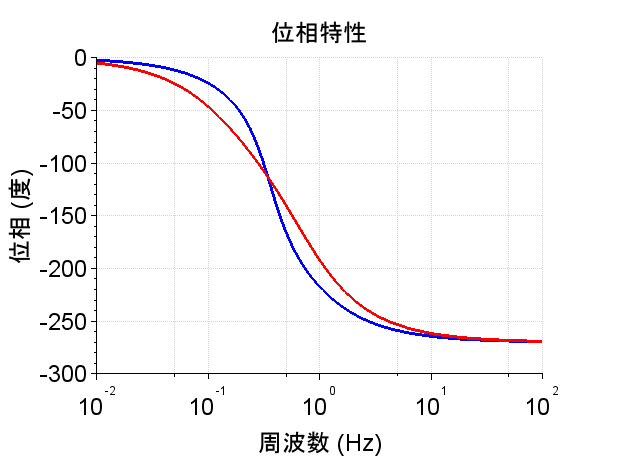
*極 \(-4 , -1 \pm 2j\)のとき伝達関数は、$$G1(s)=\frac{20}{(s+4)(s+1+2j)(s+1-2j)}$$ $$=\frac{1}{s^3 + 6s^2 +13s + 20}$$である。
*極 \(-1, -4 \pm 2j ,\)のとき伝達関数は、$$G2(s)=\frac{20}{(s+4+2j)(s+4-2j)(s+1)}$$ $$=\frac{1}{s^3 + 9s^2 +28s + 20}$$である。
代表極は、虚軸に近い極であり\(G1(s)\)の場合、 \( -1 \pm 2j\)で共役複素数である。そのため、インパルス応答が振動的になっている。一方、\(G2(s)\)の代表極は、 \(-1\)と実数である。そのため、インパルス応答は非振動的で一次遅れ系の応答に似ている。\(G1(s) , G2(s)\)とも伝達関数は3次系であるが、ステップ応答やボード線図(利得特性、位相特性)をみると、\(G1(s)\)は2次遅れ要素の特性に似ており、\(G2(s)\)は1次遅れ要素の特性に似ている。以上より、高次系の応答特性のおおよそは、代表極の複素平面上での配置によって推測できることが分かる。勿論、各々の極の配置が近い場合は、その応答特性は組み合わさったものになる。
代表極による応答特性を解析するScilabスクリプト
//代表極による時間応答特性、周波数特性
clear; clf();
s=%s;
G1=20/(s^3+6*s^2+13*s+20);
G2=20/(s^3+9*s^2+28*s+20);
G1s=syslin('c',G1);
G2s=syslin('c',G2);
t=0:0.01:10;
//インパルス応答
y1=csim('impulse',t,G1s);
y2=csim('impulse',t,G2s);
scf(0);
plot2d(t,y1,2);xgrid;
plot2d(t,y2,5);xgrid;
//ステップ応答
y1=csim('step',t,G1s);
y2=csim('step',t,G2s);
scf(1);
plot2d(t,y1,2);xgrid;
plot2d(t,y2,5);xgrid;
//ボード線図
scf(2);
gainplot([G1s;G2s],0.01,100);
scf(3);
phaseplot([G1s;G2s],0.01,100);
高域に共振点を持つ高次制御系の応答特性
\(G1(s) \cdot Gr(s)\)のボード線図
のステップ応答
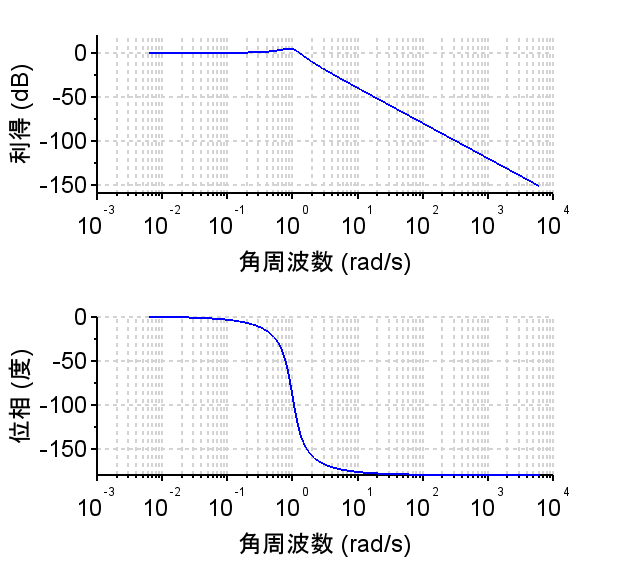
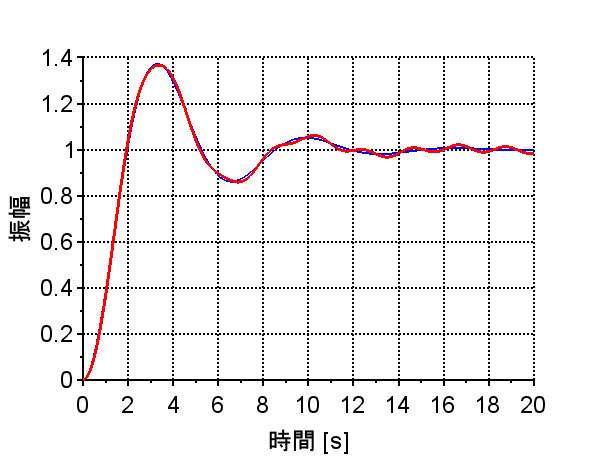
代表極が複素数である2次系\(G1(s)\)のボード線図は図のようになる。また、ステップ応答は青線で示すように滑らかに振動しながら単位ステップの1に漸近していく。
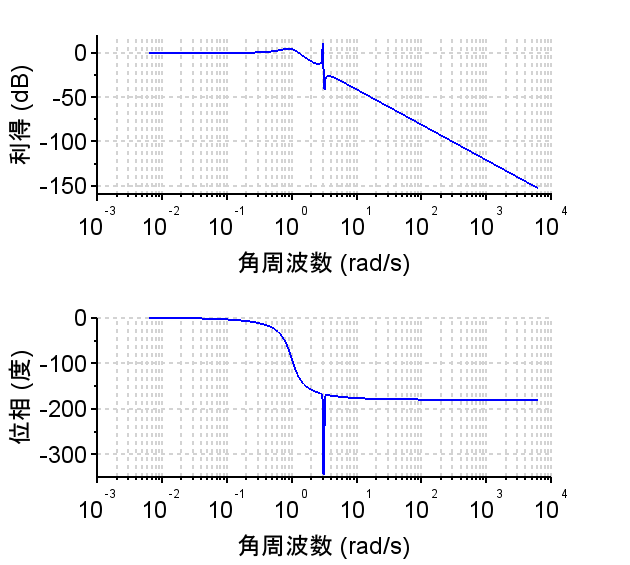
それに対して、高域に共振点を持つ2次遅れ系\(G1(s) \cdot Gr(s)\) の場合、ボード線図で角周波数が約3[rad/s]において共振点を持っており、この時のステップ応答は赤線で示すように細かな振動を伴う。
このような、高域に共振点を持つ2次遅れ系は精密機械などで良く目にする特性である。しかし、基本特性は虚軸に近い極に支配されているので、まずはこの特性を主に考えて制御器を設計することになる。
高次共振点の補償は、古典制御的にはノッチフィルタなどを用いる手段が考えられる。また、ロバスト制御ではこの共振特性も考慮した最適な制御器を設計することになる。
//2次遅れ系+高域共振点を持つ制御系の特性
clear; clf();
s=%s;
//自然角周波数 1 rad/s , 減衰係数 0.3
wn=1; zeta=0.3;
G1=(wn*wn)/(s^2+2*zeta*wn*s+wn*wn);
G1s=syslin('c',G1);
//2次遅れ系のボード線図
scf(0);
bode(G1s,'rad');
//高域共振点のモデル
wn2=3; zeta2=0.001;
Gr1=(wn2*wn2)/(s^2+2*zeta2*wn2*s+wn2*wn2);
wn3=3.2; zeta3=0.001;
Gr2=(s^2+2*zeta3*wn3*s+wn3*wn3)/(wn3*wn3);
Gr=Gr1*Gr2;
G1Gr=G1*Gr; /*2次遅れ系に高域共振点を付加*/
G1Grs=syslin('c',G1Gr);
//高域共振点を持つ2次遅れ系のボード線図
scf(1);
bode(G1Grs,'rad');
//ステップ応答
t=0:0.01:20;
y1=csim('step',t,G1s);
y2=csim('step',t,G1Grs);
scf(2);
plot2d(t,y1,2);
plot2d(t,y2,5);xgrid;


“25. 代表極(代表根)と応答特性” に対して1件のコメントがあります。
コメントは受け付けていません。