24. 安定余裕
安定判別の概要
安定判別は以下の視点から考えることができる。これらは数学的には等価な内容を含んでいる。
・インパルス応答
・伝達関数の極
・特性方程式の根(特性根)= 伝達関数の極
・特性方程式の係数から特性根を判定(ラウス・フルビッツの安定判別)
・開ループ伝達関数 \(\{L(s) \rightarrow L(j\omega) \}\)のナイキスト軌跡
・開ループ伝達関数\(\{L(s) \rightarrow L(j\omega) \}\)のベクトル軌跡
しかし、これらの考え方には、どの程度安定かという観点(ロバスト性)は含まれていない。
実際の制御系の実装には、
制御対象のモデル化誤差
制御対象の変動(温度、湿度、気圧、電圧、電流、etc.・・・)
制御器の実装誤差(素子のバラツキ、演算精度、etc.・・・)
などの要因を考慮しなければならない。そして、これらの要因によって安定なシステムが不安定にならないか、どうやって安定性を保証するかを考える必要がある。
ナイキストの安定判別の使用手順
ナイキストの安定判別の使用手順についてまとめると、以下のようになる。
1)開ループ伝達関数\(L(s)\)が不安定極を有しているか調べる。
注意:\(L(s)\)に不安定極があっても閉ループにしたら安定になることもある。
2)閉ループ系にした時、閉ループ伝達関数\(T(s)\)が不安定極を有しているか調べる。
3)\(T(s)\)に不安定極が有る場合は、\(C(s)\)を検討し、不安定極を無くす。
4)\(T(s)\)に不安定極が無い場合は、\(L(s) \rightarrow L(j\omega)\)のベクトル軌跡を描く。
5)ベクトル軌跡より、安定余裕を評価する。
この5)の安定余裕について考える。
ナイキストの安定判別法(2)(ベクトル軌跡)による安定余裕の評価
ナイキストの安定判別法(2)では、フィードバック制御系において、開ループ周波数伝達関数\(L(j\omega)\) のベクトル軌跡がどの程度の余裕をもって複素平面上の点\( (-1 , j0)\) を左に見ながら回避しているかで安定余裕を評価する。図において、点\(Q\)が\(-1\)より原点\(0\)に近くて、点\(P\)が第3象限にあると安定余裕があると評価できる。
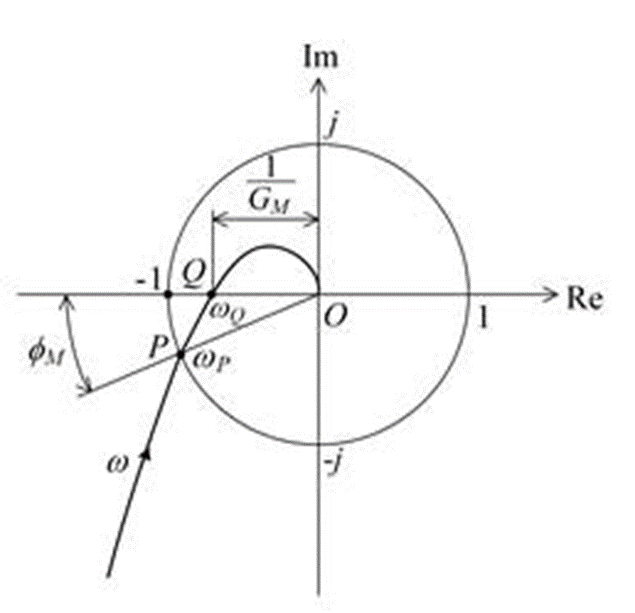
もし、\(L(j\omega) \) が\( (-1, j0)\)を通過した場合、この時の位相は\(-180^{°}\)、利得は\(1\)となる。これで単位フィードバック制御系を構成すると、\(C(s)\)への入力は正帰還となってしまい、不安定となる。(電子回路の発振回路では意図的にこのような状態を構成している。)
ベクトル軌跡が\((-1 , j0)\)を左に見て最も近づいたとき、なるべく\((-1 , j0)\) より遠い方が良い。
つまり、P、Q点を基準にして、\((-1 , j0)\) からどの程度離れているかを評価指標とする。
※利得 0dBは単位円で表せることになる
\(\omega_P\):ゲイン交差周波数
利得が\(0\)dBとなる角周波数
\(\phi_M\):位相余裕
\(\omega_Q\):位相交差周波数
位相が\(-180^{°}\)となる角周波数
\(G_M\):利得余裕
以上のように定義して、位相余裕、利得余裕で安定余裕を評価する。
ボード線図による安定余裕の評価
ベクトル軌跡による安定余裕の評価を視覚的に分かりやすくしたものが、ボード線図による安定余裕の評価である。ベクトル軌跡は、開ループ周波数伝達関数\(L(j \omega)\)において角周波数を\(\omega = 0 \sim \infty\)としたときの\(L(j \omega)\)のベクトルの先端の軌跡であるため、角周波数\(\omega\)に対するベクトルの大きさ(利得)、偏角(位相)の関係が分かりにくい。
ボード線図では、角周波数\(\omega\)に対する利得、角周波数\(\omega\)に対する位相と、ベクトル軌跡を2枚のグラフに分けて表現することで、視覚的に分かりやすくなる。
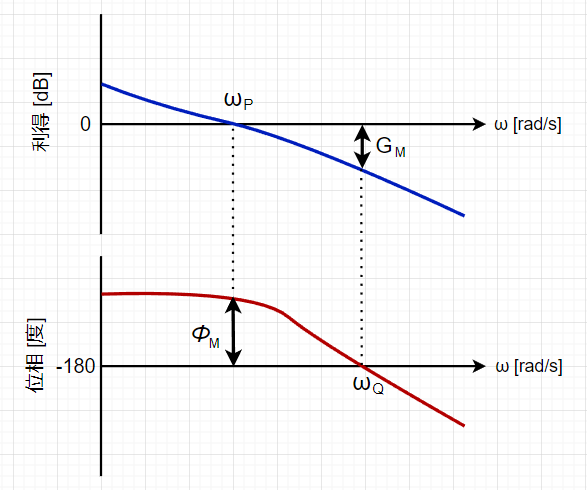
ベクトル軌跡では、角周波数(周波数)による変化を読み取り難いので、通常、ボード線図で安定余裕を評価する。
利得では、\(0\)dBを基準に、位相では、\(-180^{°}\)を基準に考える。(図の各横軸)
\(\omega_P\):ゲイン交差周波数
利得が\(0\)dBとなる角周波数
\(\phi_M\):位相余裕
\(\omega_Q\):位相交差周波数
位相が\(-180^{°}\)となる角周波数
\(G_M\):利得余裕
ベクトル軌跡での評価指標と同様に以上のように定義して、位相余裕、利得余裕で安定余裕を評価する。
位相余裕、利得余裕の目安は、制御対象の変動範囲などから経験的に以下のようになっている。
・機械制御(サーボ系):位相余裕 40~65度 、利得余裕 10~20dB
・定値制御(プロセス系):位相余裕 15~70度 、利得余裕 3~10dB
・追値制御(プロセス系):位相余裕 50度程度 、利得余裕 5~10dB
これらの目安は、様々な変動要因によって変わるため、実際には、その制御対象の変動などを計測して、妥当な位相余裕、利得余裕の仕様を決定する必要がある。一般的に、位相余裕、利得余裕を大きくとると安定性は増すが、時間応答特性では立ち上がり時間などが劣化する。
古典制御理論の範囲では、位相余裕、利得余裕の仕様を決定した後、若干の試行錯誤を通して制御器を設計することになる。(ロバスト制御理論では、変動範囲を見積もって設定することで、劣化理論的に最適な制御器を設計することができる。)
Scilabによる制御系の安定余裕評価
clear; clf;
s=%s; //開ループ伝達関数
K1=1; /*ゲイン制御器 K1*/
K2=6; /*ゲイン制御器 K2*/
L1=K1/(s*(s+1)*(s+2));
L2=K2/(s*(s+1)*(s+2));
L1s=syslin('c',L1);
L2s=syslin('c',L2);
//ベクトル軌跡
scf(0);
nyquist(L1s,'rad',%f);
scf(1);
nyquist(L2s,'rad',%f);
//開ループ周波数応答
scf(2);
bode(L1s,10^-3, 10^2,'rad');
scf(3);
bode(L2s,10^-3, 10^2,'rad');
//インパルス応答
T1=L1/(1+L1);
/*閉ループ伝達関数*/
T2=L2/(1+L2); /*閉ループ伝達関数*/
T1s=syslin('c',T1);
T2s=syslin('c',T2);
t=0:0.1:40;
y1=csim('impulse',t,T1s);
scf(4);
plot(t,y1);xgrid;
y2=csim('impulse',t,T2s);
scf(5);
plot(t,y2);xgrid;
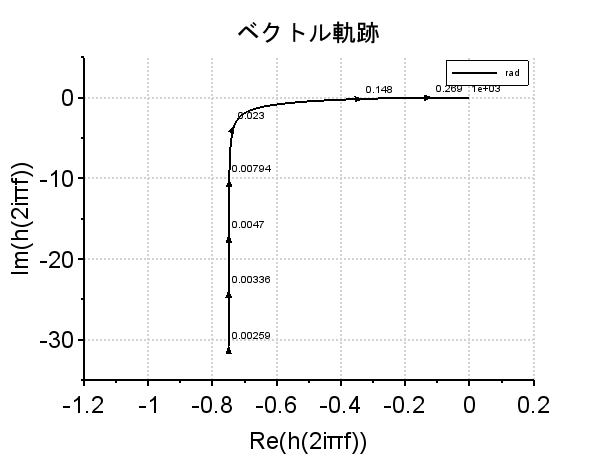
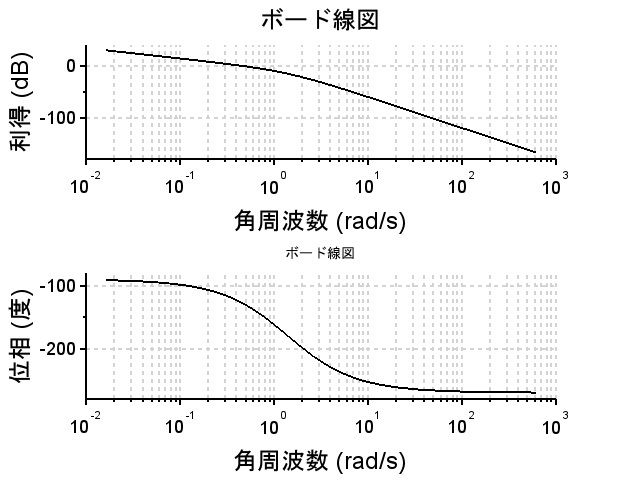
ベクトル軌跡では安定余裕がどの程度かの評価は読み取りにくい。ボード線図(K1=1で安定余裕がある場合)を見ると、ゲイン交差周波数0.7(rad/s)付近で位相余裕60度以上、位相交差周波数1.6(rad/s)付近で利得余裕10dB以上であることが読み取れる。(この図では読み取りにくいが、Scilabのスクリプトを実行したグラフでは良く分かる。)
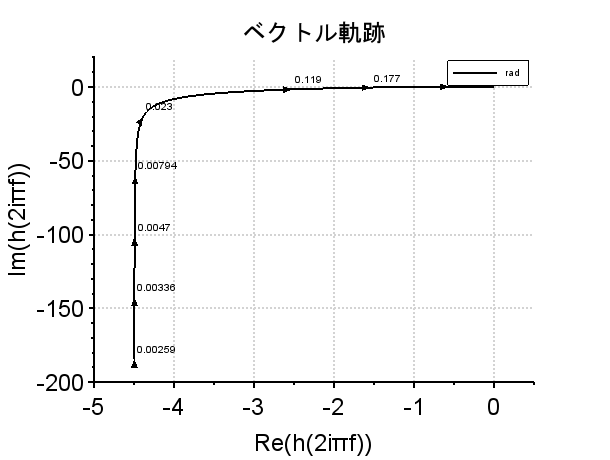
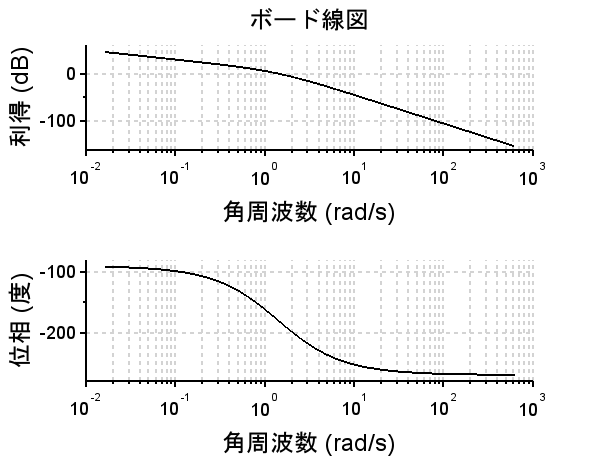
ボード線図(K2=6で安定余裕が無い場合)を見ると、ゲイン交差周波数2(rad/s)付近で位相余裕0度(すなわち、ゲイン0dBで位相が\(-180^{°}\)となっており、安定余裕の無い、安定限界となっていることがわかる。
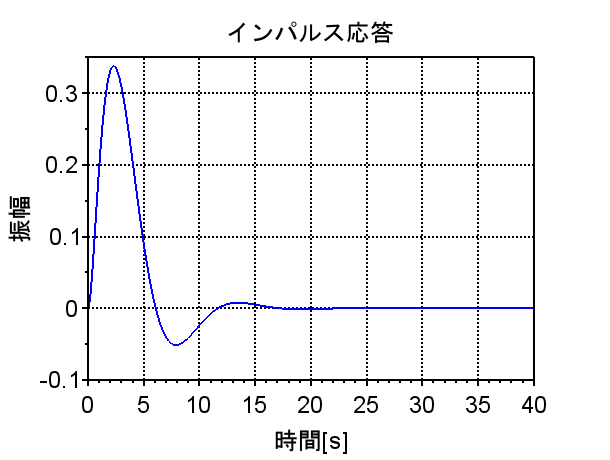
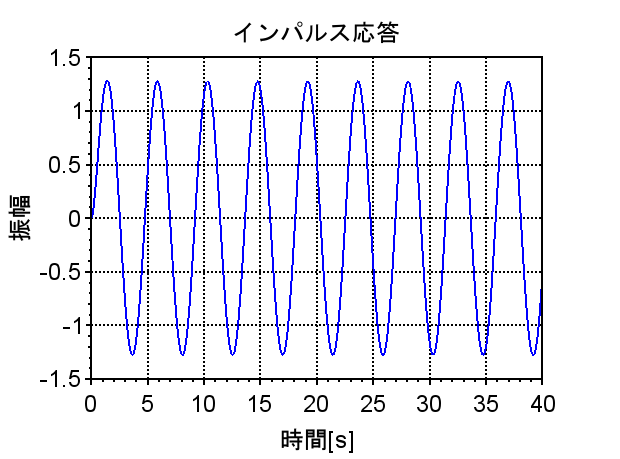
インパルス応答で確認すると、K1=1で安定余裕がある場合は、インパルス応答は時間が経つと0に収束しており、安定であることが分かる。また、振動も小さく十分に安定余裕があることが推測できる。一方、K2=6で安定余裕が無い場合は、振動が継続しており、発散はしないが安定限界にあることが分かる。

