17. 差動増幅器、ボルテージフォロワ、加算器

2023年11月26日 2023年11月26日

tctyam

オペアンプを利用した各種回路を説明する。オペアンプを使った回路の基本設計では、オペアンプを理想オペアンプと考える。また、基本的に負帰還をかけるので、入力端子$+$と$-$間は、バーチャルショート（仮想短絡）が成立しているものとする。

理想オペアンプ

・入力インピーダンス$Z_i$：$\infty$
・出力インピーダンス$Z_o$：０
・増幅度$A_o$（開ループ利得）：$\infty $

差動増幅器

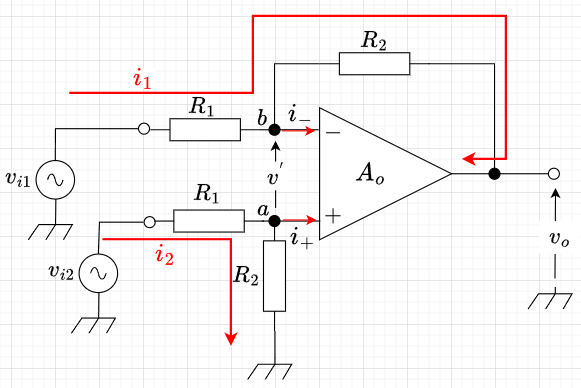
図１はオペアンプを利用した差動増幅器の基本回路図である。入力信号は、$v_{i1}$と$v_{i2}$で、これらの差を増幅して出力信号$v_o$を得る。オペアンプの入力インピーダンスは$\infty$なので、$i_+ = i_- = 0$である。そのため、図１の$a$点の電圧$v_a$は、$$v_{i2} = (R_1 + R_2) i_2 ,\;\;\;\; v_a = R_2 i_2\\ v_a = \frac{R_2}{R_1 + R_2} v_{i2}$$となる。バーチャルショートより、$b$点の電圧$v_b$は、$v_b = v_b$である。従って、$$v_{i1} - v_b = R_1 i_1 \\ v_o -v_b = -R_2 i_1$$整理すると、$$v_o = \frac{R_2}{R_1}\left(v_{i2} - v_{i1}\right) = -\frac{R_2}{R_1}\left(v_{i1} - v_{i2}\right) \;\;\;\cdots (1)$$であり、出力電圧$v_o$は、入力電圧$v_{i1}$と$v_{i2}$の差を増幅したものとなっている。
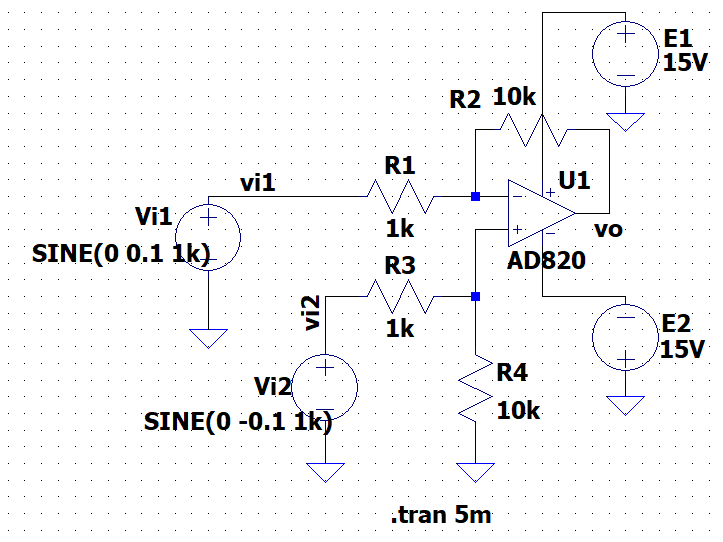
図２は、差動増幅器のLTspice回路図である。また、図３は、$v_{i1}$を振幅0.1 V、周波数1 kHzの正弦波とし、$v_{i2}$を同振幅、同周波数で逆相としたときのシミュレーション結果である。出力voは、式（1）から、$$v_o = - \frac{R2}{R1}(v_{i1} - v_{i2}) = -10(v_{i1} - v{i2})$$なので、振幅2.0 Vの正弦波となる。また、$-10$倍なので、$v_o$と$v_{i1}$は逆相となる。なお、$v_{i1}$と$v_{i2}$が同振幅、同周波数、同位相なら$v_o$は、ほぼ０となる。

図３　シミュレーション結果
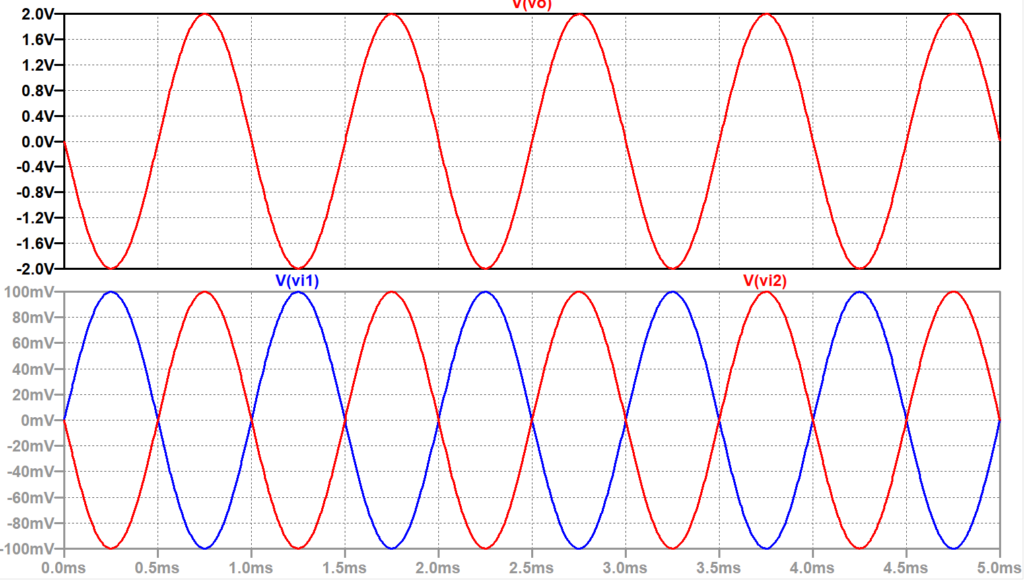
$v_{i1},\;v_{i2}$：下、$v_o$：上

ボルテージフォロワ

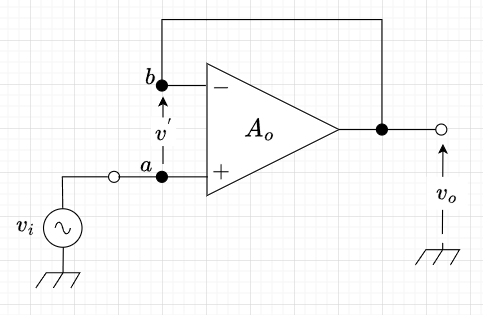
図４がボルテージフォロワの回路図である。ボルテージフォロワでは、$$v_i = v_o$$となり、電圧増幅度は１である。電流増幅度はオペアンプ自体の仕様による。ボルテージフォロワの特徴は、
・入力インピーダンスは非常に大きい：$Z_i = \infty$
・出力インピーダンスは非常に小さい：$Z_o=0$
・電圧増幅度１（$0\; dB$）
である。インピーダンス変換器として使用することが多い。
図５は非反転増幅回路の回路図である。この回路の電圧増幅度は、$$A_{vf} =1 + \frac{R2}{R1} \;\;\;\cdots (2)$$である。ここで、$R_1$を取り外し、$R_2 = R_3 = 0$とすると、図４のボルテージフォロワになる。電圧増幅度は、式（2）で$R_1 = \infty$とすると、$$A_{vf} = 1$$となることがわかる。図４で考えると、$Z_i = \infty$より、$a$点の電圧は$v_i$であり、バーチャルショート（$v^{'}=0$）より、$b$点の電圧は$v_i$である。その結果、$v_o = v_i$となる。

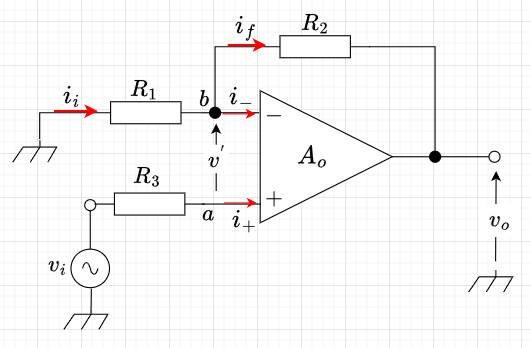
加算器

図６は、２入力の加算器である。昔は、アナログコンピュータの加算器として使われていた。
図６より、バーチャルショートが成立しているとすると、$a$点の電圧$v_a$と$b$点の電圧$v_b$は等しいので、$v_b = 0$である。また、オペアンプの入力インピーダンス$Z_i =\infty$なので、$i_f = i_1 + i_2$である。$$i_1 = \frac{v_1}{R_1} ,\;\; i_2 = \frac{v_2}{R_1} \\ v_o = - i_f R_f = -(i_1 + i_2)R_f\\ v_o=-\left(\frac{v_1}{R_1} + \frac{v_2}{R_1} \right)R_f= - \frac{R_f}{R_1}(v_1 + v_2)$$となる。$R_f = R_1$とすれば、$v_o = v_1 + v_2$と出力電圧は２つの入力電圧の和となる。

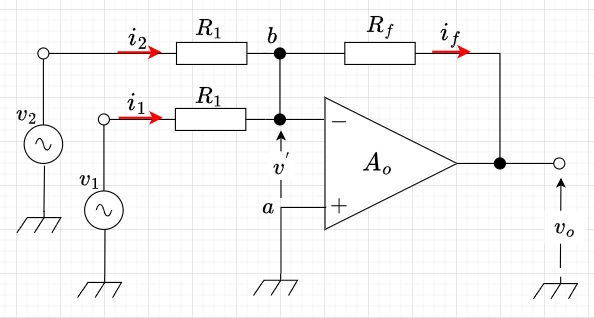
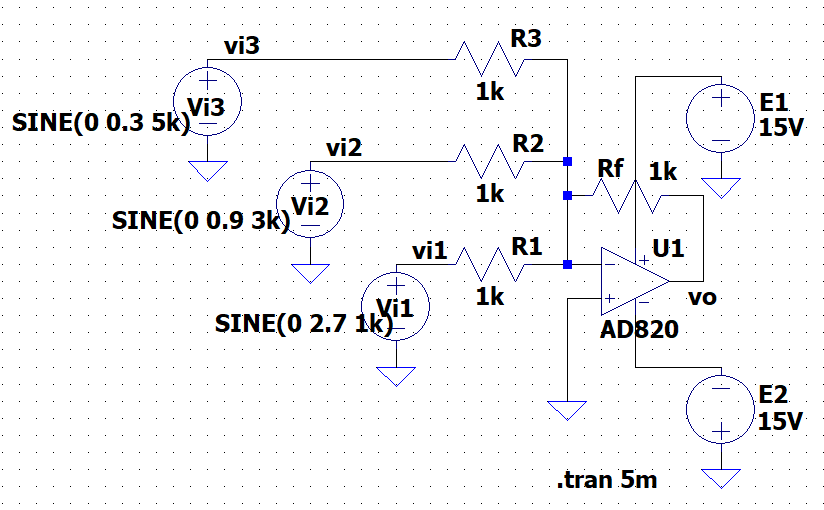
図７は、LTspiceの加算器回路図である。3入力の振幅、周波数を変えて加算している。$R_1 = R_2 = R_3 = R_f$としているので、増幅度は１である。
入力電圧は正弦波で、基本周波数は$1\;kHz$として$v_{i1},\;\;v_{i2},\;\;v_{i3}$は、$$\omega = 2 \pi \times 1000 \\v_{i1} = 2.7\sin(\omega t) \;\;\;\;\;\;\; v_{i2} = 0.9\sin(3 \omega t) \;\;\;\;\;\;\; v_{i3} = 0.3\sin(5 \omega t)$$である。
図８はシミュレーション結果である。これは、フーリエ級数を利用して、正弦波の合成で方形波を近似している。入力数をさらに増やせば、方形波に近づく。

図８　シミュレーション結果（加算器）
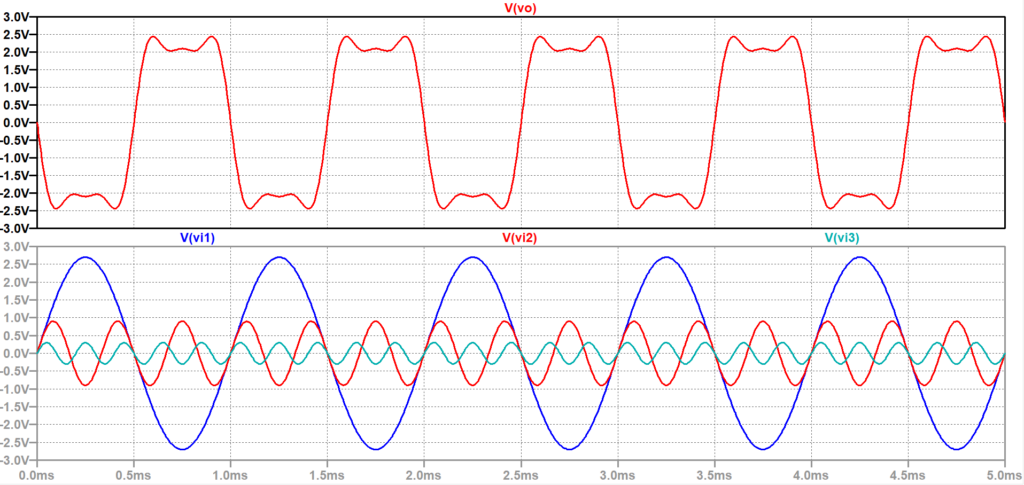
$v_{i1},\; v_{i2},\; v_{i3}$：下、$v_o$：上

フーリエ級数展開

フーリエ級数（Fourier series）は、周期的な関数を三角関数の無限級数で表現するための数学的手法である。
周期$T$を持つ関数$f(t)$が与えられた場合、そのフーリエ級数表示は以下である。
$$f(t) = a_0 + \sum_{n=1}^{\infty} \left( a_n \cos n \omega t+ b_n \sin n \omega t \right)\\ \omega = 2 \pi \frac{1}{T} = 2 \pi f$$ここで、各係数 $a_0,\; a_n,\; b_n$はフーリエ係数である。これらの係数は以下のようになる。$$a_0 = \frac{1}{T} \int_{-\frac{T}{2}} ^{\frac{T}{2}} f(t)dt \\ a_n = \frac{2}{T} \int_{-\frac{T}{2}} ^{\frac{T}{2}} f(t) \cos n \omega t dt \\ b_n = \frac{2}{T} \int_{-\frac{T}{2}} ^{\frac{T}{2}} f(t) \sin n \omega t dt \\ (n = 1,2,3, \cdots)$$ これらの式は、関数$f(t)$を三角関数の無限級数で表現する際に、それぞれの三角関数成分の寄与を表している。この無限級数で十分な項を取ることにより、元の関数$f(t)$に近似することができる。

フーリエ係数の導出

$a_n$を求めるために、$$f(t) = a_0 + \sum_{n=1}^{\infty} \left( a_n \cos n \omega t+ b_n \sin n \omega t \right)$$この両辺に$\cos m \omega t$を掛けると、$$f(t) \cos m \omega t = \left\{ a_0 + \sum_{n=1}^{\infty} \left( a_n \cos n \omega t+ b_n \sin n \omega t \right) \right\} \cos m \omega t$$ 両辺を積分する。$$\int_{-\frac{T}{2}}^{\frac{T}{2}} f(t) \cos m \omega t dt = \int_{-\frac{T}{2}}^{\frac{T}{2}} \left\{ a_0 + \sum_{n=1}^{\infty} \left( a_n \cos n \omega t+ b_n \sin n \omega t \right) \right\} \cos m \omega t dt \\ = \int_{-\frac{T}{2}}^{\frac{T}{2}} a_0 \cos m \omega t dt + \sum_{n=1}^{\infty} \int_{-\frac{T}{2}}^{\frac{T}{2}} \left( a_n \cos n \omega t+ b_n \sin n \omega t \right) \cos m \omega t dt \\ = \int_{-\frac{T}{2}}^{\frac{T}{2}} a_0 \cos m \omega t dt + a_m \frac{T}{2} = a_m \frac{T}{2}$$よって、$m$を$n$に置き変えると、$$ a_n = \frac{2}{T} \int_{-\frac{T}{2}} ^{\frac{T}{2}} f(t) \cos n \omega t dt$$となる。
次に、$b_n$を求めるために、$$f(t) = a_0 + \sum_{n=1}^{\infty} \left( a_n \cos n \omega t+ b_n \sin n \omega t \right)$$この両辺に$\sin m \omega t$を掛けると、$$f(t) \sin m \omega t = \left\{ a_0 + \sum_{n=1}^{\infty} \left( a_n \cos n \omega t+ b_n \sin n \omega t \right) \right\} \sin m \omega t$$ 両辺を積分する。$$\int_{-\frac{T}{2}}^{\frac{T}{2}} f(t) \sin m \omega t dt = \int_{-\frac{T}{2}}^{\frac{T}{2}} \left\{ a_0 + \sum_{n=1}^{\infty} \left( a_n \cos n \omega t+ b_n \sin n \omega t \right) \right\} \sin m \omega t dt \\ = \int_{-\frac{T}{2}}^{\frac{T}{2}} a_0 \sin m \omega t dt + \sum_{n=1}^{\infty} \int_{-\frac{T}{2}}^{\frac{T}{2}} \left( a_n \cos n \omega t+ b_n \sin n \omega t \right) \sin m \omega t dt \\ = \int_{-\frac{T}{2}}^{\frac{T}{2}} a_0 \sin m \omega t dt + b_m \frac{T}{2} = b_m \frac{T}{2}$$よって、$m$を$n$に置き変えると、$$ b_n = \frac{2}{T} \int_{-\frac{T}{2}} ^{\frac{T}{2}} f(t) \sin n \omega t dt$$となる。
さらに、$a_0$を求めるために、$$f(t) = a_0 + \sum_{n=1}^{\infty} \left( a_n \cos n \omega t+ b_n \sin n \omega t \right)$$この両辺を積分する。$$\int_{-\frac{T}{2}}^{\frac{T}{2}} f(t) dt = \int_{-\frac{T}{2}}^{\frac{T}{2}} \left\{ a_0 + \sum_{n=1}^{\infty} \left( a_n \cos n \omega t+ b_n \sin n \omega t \right) \right\} dt \\ = \int_{-\frac{T}{2}}^{\frac{T}{2}} a_0 dt + \sum_{n=1}^{\infty} \int_{-\frac{T}{2}}^{\frac{T}{2}} \left( a_n \cos n \omega t+ b_n \sin n \omega t \right) dt \\ = \int_{-\frac{T}{2}}^{\frac{T}{2}} a_0 dt = a_0 T$$よって、$$a_0 = \frac{1}{T} \int_{-\frac{T}{2}}^{\frac{T}{2}} f(t) dt$$となる。

フーリエ級数展開例

方形波

方形波（Square Wave）（図９）は、周期 $T$で周期的に変化する信号で、一定の振幅を持つ部分が$T/2$ の時間だけ正の振幅を持ち、残りの$T/2$の時間は負の振幅を持つ波形である。
方形波のフーリエ級数展開は、$$f(t) = \frac{4}{\pi} \sum_{n=1,3,5,\dots}^{\infty} \frac{\sin n \omega_0 t}{n}$$となる。

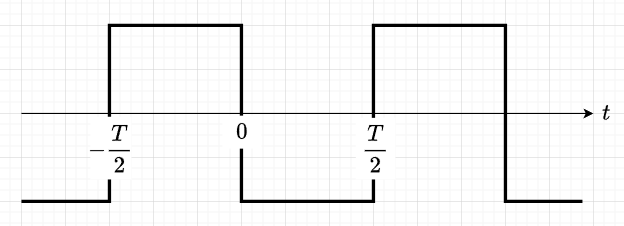
ここで、$f(t)$は方形波の関数、$f_0$は方形波の基本周波数で、$f_0 = \frac{1}{T} ,\;\;\; \omega_0 = 2 \pi f_0$ である。（$T$ は方形波の周期）
このフーリエ級数展開は、奇数の倍数のサイン関数の無限和で表されている。各項は$\frac{1}{n}$の係数を持ち、$n$が増えるにつれて高次の成分が加わる。

三角波

三角波（Triangle Wave）（図１０）は周期的な波形である。
三角波のフーリエ級数展開は、$$f(t) = \frac{8}{\pi ^2} \sum_{n = 1,3,5,\dots}^{\infty} \frac{\sin (2n-1)\omega_0 t}{(2n-1)^2}$$となる。

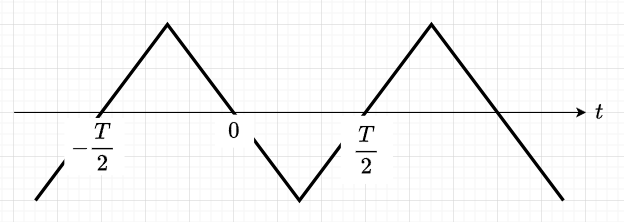
ここで、$f(t)$は三角波の関数、$\omega_0$は三角波の基本角周波数で、$\omega_0 = \frac{2 \pi}{T}$である。（$T$は三角波の周期）
このフーリエ級数展開では、奇数の倍数のサイン関数の無限和で表されています。各項は$\frac{1}{(2n -1)^2}$ の係数を持ち、$n$ が増えるにつれて高次の成分が加わる。

カテゴリー: 電子回路の基礎