39. 過渡現象
過渡現象とは、ある定常状態から別の定常状態に移るまでに起こる現象のことを言う。電気回路では、スイッチを切り替えたときなどに起こる。
過渡現象は、回路の安定性に影響を及ぼす可能性がある。また、過渡現象が原因で、回路が誤動作したり、故障したりすることもありえる。
過渡現象を防ぐためには、回路の設計時に、過渡現象の影響を考慮する必要があり、過渡現象が発生した場合は、適切な対策を講じることが重要である。
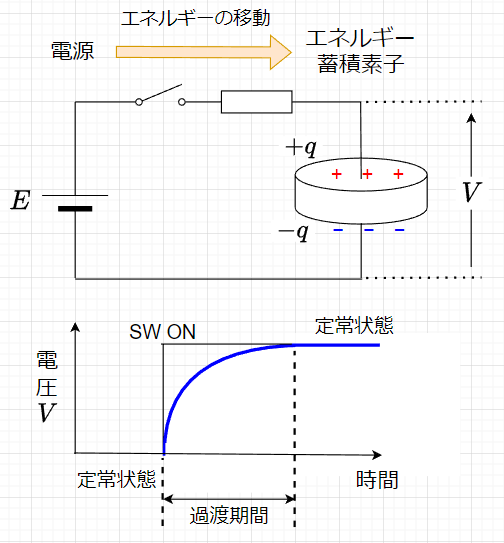
図「過渡現象」で、過渡現象の例を考える。この回路では、エネルギー蓄積素子であるコンデンサ(キャパシタ)が接続されている。このような回路では、回路中の電圧や電流が急激に変化して、回路の状態が定常状態からほかの定常状態に移行しようとしても、エネルギー蓄積素子中のエネルギーが増減するために、ある時間を必要とする。この移行期間を過渡期間といい、この間に起こる現象を過渡現象という。図では、スイッチを入れたところから、定常状態になるまでの期間が過渡期間である。スイッチを入れるとコンデンサに電荷が移動(回路に電流が流れる)し、徐々にコンデンサの両端の電圧が上昇し、電源電圧\(E\)とコンデンサ両端の電圧\(V\)が等しくなると電荷の移動が止まり、定常状態になる。
R-C直列回路の過渡現象
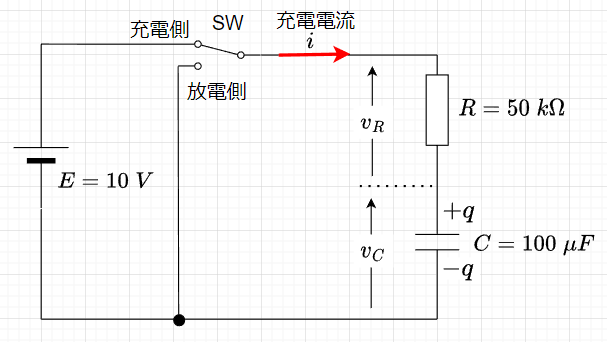
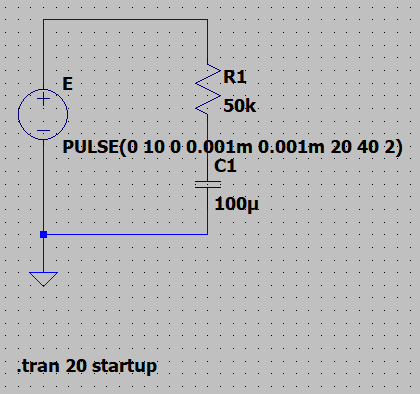
図「RーC直列回路」において、スイッチ(SW)を放電側に入れて、\(C\)に残っている電荷を放電し、零にしておく。つぎにスイッチを充電側に切り換えると、\(C\)には電源\(E\)から電荷\(q\;[C]\)が、抵抗\(R\)の制限を受けながら蓄えられる。この電荷の移動は、\(C\)の端子電圧\(v_C \;[V]\)が電源電圧\(10\;V\)になるまで続き、この間、充電電流\(i\)が流れる。
この過渡現象をLTspiceによってシミュレーションする。
スイッチを充電側に入れてから、次の定常状態に移行するまでの電流\(i\)(青線)と\(C\)の端子電圧\(v_C\)(緑線)の時間変化を図「コンデンサの充電特性」に示す。この図からコンデンサ\(C\)が次第に充電され、端子電圧\(v_C\)(緑線)が上昇し、電源の電圧\(E\)に等しくなることを示している。
スイッチを充電側に入れた瞬間は、\(C\)に蓄えられた電荷\(q\)は0であるから、\(v_C\)も0である。従って、電源の電圧\(E\)は、抵抗\(R\)にだけ加わることになるから、充電電流\(i\)は、$$i=\frac{v_R}{R} = \frac{E}{R} = \frac{10}{50\times 10^3}=200 \;\mu A$$となる。\(v_C\)が上昇するにつれて充電電流\(i\)(青線)は減少し、最終的には\(i=0\)になり充電が完了する。\(i, v_R,v_C\)は以下の式で表せる。$$i=\frac{E}{R}e^{-\frac{1}{RC}t} \; [A] \\ v_R = R i = Ee^{-\frac{1}{RC}t} \;[V] \\ v_C = E (1-e^{-\frac{1}{RC}t}) \; [V] \cdots(1)$$
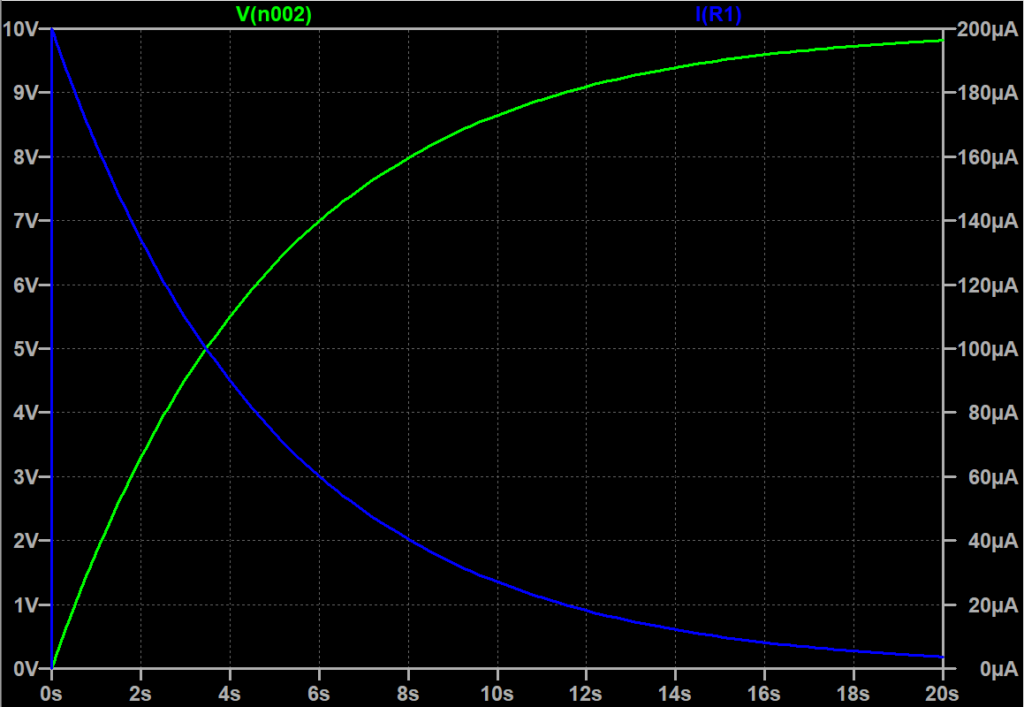
いま、式(1)において、\(t=RC\;[s]\)のときには、$$v_C = E(1 - e^{-\frac{1}{RC}\cdot RC}) = E(1 - e^{-1}) \simeq E(1 - 0.368) = 0.632E \;[V]$$となる。\(v_C\)が電源電圧\(E\)の63.2%に達するまでの時間\(\tau\;[s]\)を時定数という。$$\tau = RC \;[s]$$時定数は、過渡現象の変化の速さを知るめやすとなる値である。
R-L直列回路の過渡現象
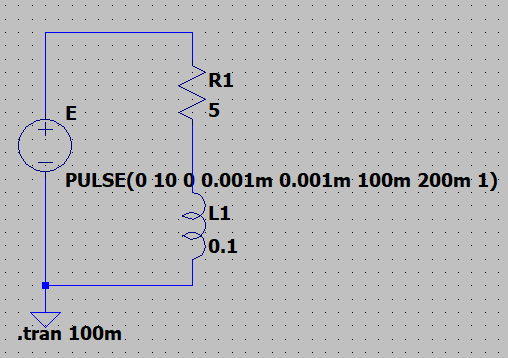
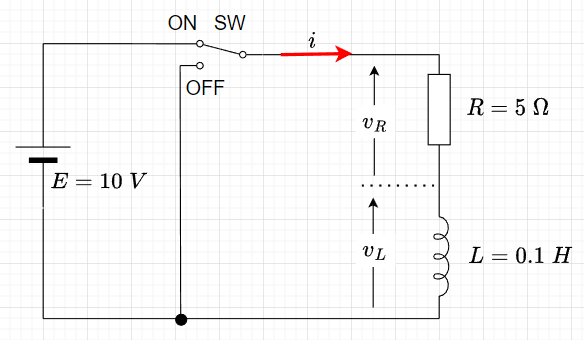
図「RーL直列回路」のように抵抗\(R \;[\Omega]\)とコイル(インダクタ)\(L \; [H]\)の直列回路において、スイッチ(SW)をON側に入れると、回路の電流\(i \;[A]\)は、定常値\(\frac{E}{R} \;[A]\)に向かって増加する。しかし、電流が変化すると、回路のインダクタンス\(L\)により逆起電力が生じて、電流の増加を妨げるので、電流は徐々に\(\frac{E}{R} \;[A]\)に近づく。
この過渡現象をLTspiceによってシミュレーションする。
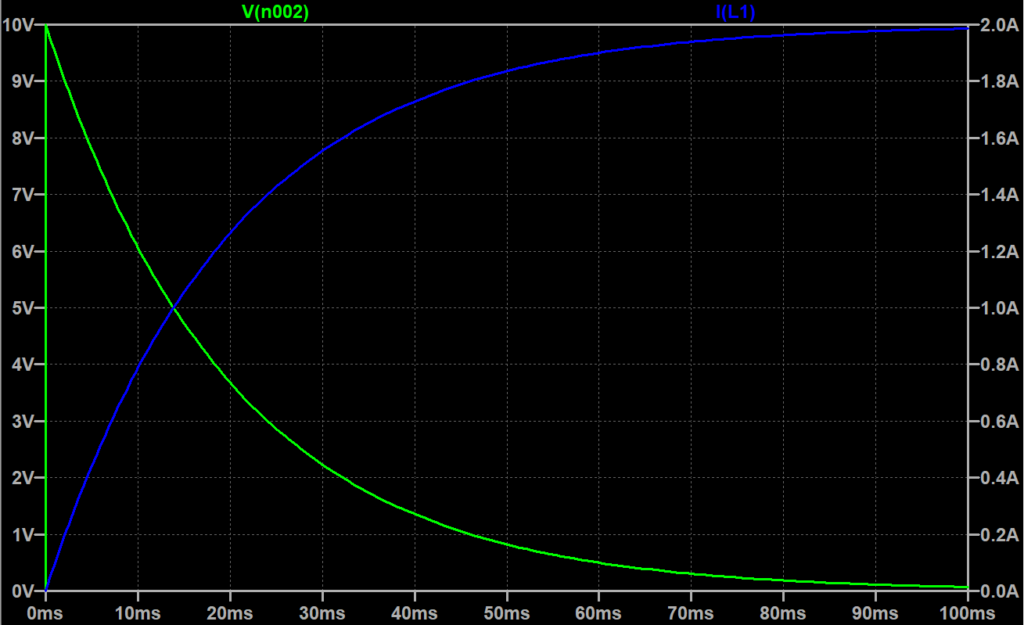
スイッチをONにしてから、つぎの定常状態に移行するまでの電流\(i\)(青線)と\(L\)の端子電圧\(v_L\)(緑線)の時間的変化を図「RーL直列回路の電圧、電流特性」に示す。
\(i, v_R, v_L\)は以下の式で表せる。$$i = \frac{E}{R}(1 - e^{-\frac{R}{L}t}) \; [A] \cdots (2) \\ v_R = R i =E(1 - e^{-\frac{R}{L}t}) \; [V] \\v_L = E - v_R = Ee^{-\frac{R}{L}t} \; [V]$$式(2)において、\(t = \frac{L}{R}\)のとき、電流\(i\)は$$ i = \frac{E}{R}(1 - e^{-\frac{R}{L} \cdot \frac{L}{R}}) \\= \frac{10}{5}(1 - e^{-1}) = 2 \times 0.632 =1.26\; A$$となる。この回路の時定数\(\tau\)は、$$\tau = \frac{L}{R} \; [s]$$となる。この回路の場合、$$\tau = \frac{L}{R} = \frac{0.1}{5} = 20 \;ms$$となる。