25. RL直列回路、RC直列回路
直列回路
\(R\)だけの直列接続
図「直列抵抗回路」のように、抵抗\(R_1,R_2,R_3\)を直列に接続した場合の合成抵抗\(R\)は、直流回路の場合と同様で、$$R = R_1 +R_2 + R_3 \; [\Omega]$$と表せる。
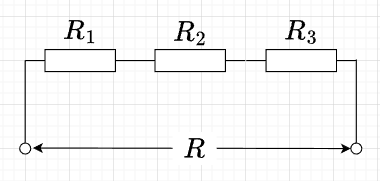
\(L\)だけの直列接続
図「直列インダクタ回路」のように、インダクタ\(L_1,L_2,L_3\)を直列に接続した場合の合成インダクタンス\(L\)は、$$L = L_1 + L_2 +L_3$$である。この両辺に\(\omega\)を乗じると、$$\omega L = \omega L_1 + \omega L_2 + \omega L_3$$となる。よって、$$X_L = X_1 + X_2 +X_3 \;[\Omega]$$である。従って、直列の誘導性リアクタンスは、各インダクタンスのリアクタンスの和に等しくなる。
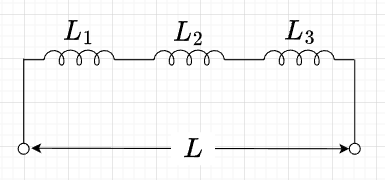
\(C\)だけの直列接続
図「直列キャパシタ回路」のように、キャパシタ\(C_1,C_2,C_3\)を直列に接続した場合の合成キャパシタンス\(C\)は、$$\frac{1}{C} =\frac{1}{C_1} + \frac{1}{C_2} + \frac{1}{C_3}$$となる。この両辺に\(\frac{1}{\omega}\)を乗じると、$$\frac{1}{\omega C} = \frac{1}{\omega C_1} + \frac{1}{\omega C_2} + \frac{1}{\omega C_3}$$である。よって、$$X_c= X_1 + X_2 + X_3 \;[\Omega]$$である。従って、直列の容量性リアクタンスは、各キャパシタンスのリアクタンスの和に等しくなる。
性質の異なる素子を直列に接続する場合、誘導性リアクタンスでは電圧は電流より\(\pi/2\)進み、容量性リアクタンスでは\(\pi/2\)遅れるので、電圧、電流は位相を考えてベクトル的に取り扱わなければならない。従って、リアクタンスを単に加え合わせるだけの計算ではなくなる。
\(RL\)直列回路
図「\(RL\)直列回路」のように抵抗\(R \; [\Omega]\)とインダクタンス\(L \; [H]\)とが直列に接続された回路に\(e = E_m \sin (\omega t + \theta) \; [V]\)の電圧を加えた場合を考える。
この回路に流れる電流を\(i = I_m \sin \omega t \; [A]\)とすると、\(R\)の両端の電圧は、$$e_R = R I_m \sin \omega t $$また、\(L\)の両端の電圧は、$$e_L = \omega L I_m \sin \left( \omega t + \frac{\pi}{2} \right) = \omega L I_m \cos \omega t$$
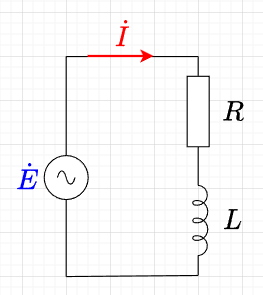
回路全体に加わる電圧は、\(e_R\)と\(e_L\)の和であるから、$$e = e_R + e_L = R I_m \sin \omega t + \omega L I_m \cos \omega t \\ = \sqrt{R^2 + (\omega L)^2} I_m \left(\frac{R}{\sqrt{R^2 + (\omega L)^2} } \sin \omega t + \frac{\omega L}{\sqrt{R^2 + (\omega L)^2} } \cos \omega t \right) \; [V] \;\;\cdots\cdots (1)$$となる。
図「三角比」を参照すると、$$\sin \theta = \frac{\omega L}{\sqrt{R^2 + (\omega L)^2} } , \;\;\;\;\; \cos \theta = \frac{R}{\sqrt{R^2 + (\omega L)^2} } , \\ \tan \theta = \frac{\omega L}{R}$$
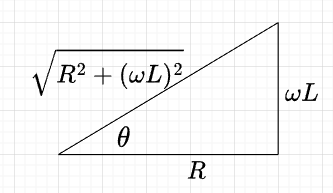
となるので、式\((1)\)は、$$e = \sqrt{R^2 + (\omega L)^2} I_m (\cos \theta \sin \omega t + \sin \theta \cos \omega t) \\=\sqrt{R^2 +(\omega L)^2} I_m \sin (\omega t + \theta) \; [V] \\ \theta = \tan^{-1} \frac{\omega L}{R}$$と表せる。このように電流を基準にとると、電圧は\(\theta\)だけ位相が進むことになる。
これをベクトルで表記する。電流\(\dot{I}\)とすると、\(R\)の両端の電圧は、\(E_R = I R\)、\(L\)の両端の電圧は、\(E_L = X_L I = \omega L I\)であり、位相は、\(\dot{E}_R\)は\(\dot {I}\)と同相で、\(\dot{E}_L \)は\(\dot{I}\)より\(\pi/2\) 位相が進んでいる。
(※ここで、ベクトル表記では電流、電圧とも実効値である。)
この関係をベクトル図にすると、図「\(RL\)直列回路のベクトル図」となる。\(\dot{E}_R\)と\(\dot{E}_L\)をベクトルで加算すると\(\dot{E}\)となる。すなわち、$$\dot{E}_R + \dot{E}_L = \dot{E} \; [V]$$であり、大きさの関係は、$$E =\sqrt{{E_R}^2 + {E_L}^2} = \sqrt{(RI)^2 + (X_L I)^2} \\= \sqrt{R^2 + {X_L}^2} I = \sqrt{R^2 + (\omega L)^2} I \; [V]$$
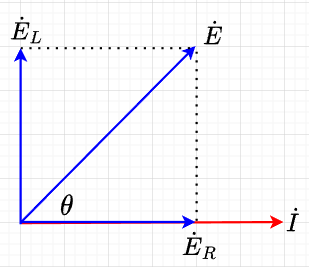
$$I = \frac{E}{\sqrt{R^2 + (\omega L)^2} }\; [A] \;\;\;\;\;\; \theta = \tan^{-1} \frac{E_L}{E_R} = \tan^{-1} \frac{\omega L}{R}$$ここで、\(Z = \sqrt{R^2 + (\omega L)^2}\)とおくと、$$I= \frac{E}{Z} \; [A] \;\;\;\;\; E=ZI \; [V]$$となり、直流回路のオームの法則と同じ形で表せる。この\(Z\)をインピーダンスと呼び、単位は\(\Omega\)である。
\(RC\)直列回路
図「\(RC\)直列回路」のように、抵抗\(R \; [\Omega]\)と静電容量\(C \; [F]\)が直列に接続された回路に\(\dot{E} \;[V]\)の電圧を加えたとき、電流\(\dot{I} \; [A]\)が流れたとすると、\(R\)両端の電圧は、$$E_R = R I \; [V]$$\(C\)の両端の電圧は、$$E_C = X_C I = I / \omega C \;[V]$$となる。また、\(\dot{E}_R\)は\(\dot{I}\)と同相、\(\dot{E}_C\)は\(\dot{I}\)より\(\pi /2\) 遅れる。
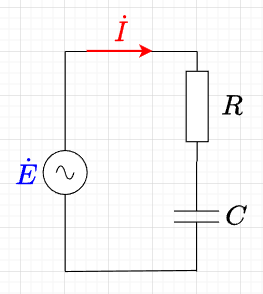
ベクトル図で表すと図「\(RC\)直列回路のベクトル図」のようになる。従って、供給電圧と電流の大きさの関係は、$$E = \sqrt{{E_R}^2 + {E_C}^2} = \sqrt{(RI)^2 + (X_c I)^2} \\ = \sqrt{R^2 +\left(\frac{1}{\omega C}\right)^2 }I \; [V] $$ $$ I =\frac{E}{\sqrt{R^2 + \left( \frac{1}{\omega C}\right)^2 }} \; [A]$$となる。
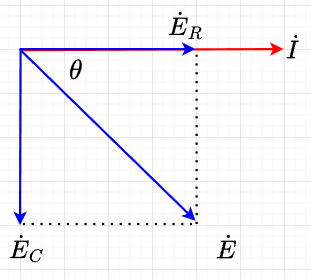
このとき、\(\dot{E}\)と\(\dot{I}\)の位相の関係は、$$\theta = \tan^{-1} \frac{E_C}{E_R} = \tan^{-1} \frac{\frac{1}{\omega C}}{R} = \tan^{-1} \frac{1}{\omega CR}$$である。
また、この場合のインピーダンスは、$$Z=\sqrt{R^2 + \left(\frac{1}{\omega C}\right)^2} \; [\Omega]$$である。

