3. 抵抗の直列接続、並列接続
抵抗の直列接続とは、複数の抵抗が一列に直列につながれている状態を指す。この場合、同じ電流が全ての抵抗を流れ、各抵抗での電圧降下の合計が全電圧に等しくなる。つまり、直列接続された抵抗の合成抵抗は、各抵抗の抵抗値を足し合わせたものになる。
抵抗の並列接続とは、複数の抵抗が平行に並列につながれている状態を指す。この場合、各抵抗には同じ電圧がかかり、全体の電流は各抵抗の電流の総和になる。つまり、並列接続された抵抗の合成抵抗は、各抵抗の逆数を足し合わせたものの逆数になる。
直列接続は、電気回路で電圧を分割するのに適しており、並列接続は、電気回路で電流を分割するのに適している。
直列接続
回路図の読み方の基本、回路図中の記号の意味
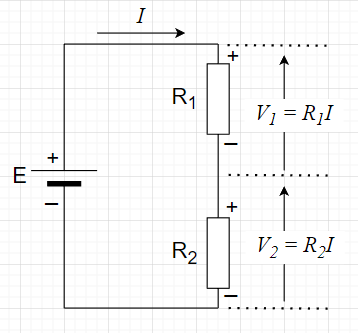
回路図を読む場合、電気部品記号、量記号(\(R \;,\;E \;,\;I\)など)、値(\(1\; k\Omega\)など、記載しない場合もある)に注目する。各電気部品記号間を繋いでいる線は部品間の接続関係を表した仮想線である。この仮想線と回路を実装する場合の実際の配線は異なる。
図中の「+」は電圧が高い方、「ー」は電圧が低い方を表している。また、電流の矢印は電流の流れる方向を表している。電圧の矢印では、電圧が高い方を鏃(やじり)で、電圧が低い方を矢筈(やはず)で表している。これらは説明のための記号で、実際の回路図には、通常、記載しない。
図「抵抗2個の直列接続」で考える。\(E\)は起電力\(E \;[V]\)の電源、\(R_1 \;,\; R_2\)が抵抗である。
直列接続なので、同じ電流\(I\)が抵抗\(R_1 \;,\; R_2\)に流れる。オームの法則により、抵抗\(R_1\)の電圧降下は、\(V_1 = R_1 I\)、抵抗\(R_2\)の電圧降下は、\(V_2= R_2 I\)となる。また、各抵抗での電圧降下の合計が全電圧であり、\(E = V_1 + V_2\)となる。
$$E = R_1I + R_2 I = (R_1 + R_2)I$$より。直列接続の合成抵抗は、$$R_s = \frac{E}{I} = R_1 + R_2$$となる。
また、$$I = \frac{E}{R_s} = \frac{E}{R_1 + R_2}$$なので、各抵抗の電圧降下は、$$V_1 = R_1 I = \frac{R_1}{R_1 + R_2} E$$ $$V_2 = R_2 I = \frac{R_2}{R_1 + R_2} E$$となる。これを分圧の式という。
抵抗の直列接続
\(n\)個の抵抗を直列接続したときの合成抵抗は、$$R_s = R_1 + R_2 + \cdots + R_n$$となる。また、\(R = R_1 = R_2 = \cdots \)を\(n\)個 直列接続した場合の合成抵抗は、$$R_s = n \times R$$となる。
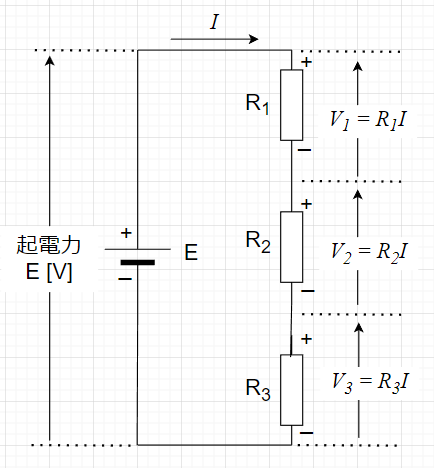
図「抵抗3個の直列接続」で考える。\(E\)は起電力\(E \;[V]\)の電源、\(R_1 \;,\; R_2\;,\;R_3\)が抵抗である。
直列接続なので、同じ電流\(I\)が抵抗\(R_1 \;,\; R_2\;,\;R_3\)に流れる。オームの法則により、抵抗\(R_1\)の電圧降下は、\(V_1 = R_1 I\)、抵抗\(R_2\)の電圧降下は、\(V_2= R_2 I\)、抵抗\(R_3\)の電圧降下は、\(V_3= R_3 I\)となる。また、各抵抗での電圧降下の合計が全電圧であり、\(E = V_1 + V_2 + V_3\)となる。
$$E = R_1I + R_2 I + R_3I= (R_1 + R_2 + R_3)I$$より。直列接続の合成抵抗は、$$R_s = \frac{E}{I} = R_1 + R_2 + R_3$$となる。
*分圧の式は、$$I = \frac{E}{R_s} = \frac{E}{R_1 + R_2 + R_3}$$なので、$$V_1 = R_1 I = \frac{R_1}{R_1 + R_2 + R_3} E$$ $$V_2 = R_2 I = \frac{R_2}{R_1 + R_2 + R_3} E$$ $$V_3 = R_3 I = \frac{R_3}{R_1 + R_2 + R_3} E$$となる。
並列接続
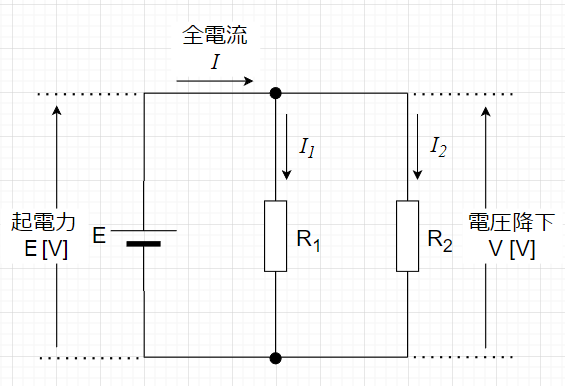
図「抵抗2個の並列接続」で考える。\(E\)は起電力\(E \;[V]\)の電源、\(R_1 \;,\; R_2\)が抵抗である。
並列接続なので、同じ電圧\(E\)が抵抗\(R_1 \;,\; R_2\)に印可される。オームの法則により、抵抗\(R_1\)に流れる電流は、\(I_1 =\frac{E}{R_1} \)、抵抗\(R_2\)に流れる電流は、\(I_2= \frac{E}{R_2}\) となる。また、各抵抗に流れる電流の合計が全電流であり、\(I = I_1 + I_2\)となる。$$I = I_1 + I_2 = \frac{E}{R_1} + \frac{E}{R_2} \\ = \left(\frac{1}{R_1} + \frac{1}{R_2}\right)E$$並列接続の合成抵抗を\(R_p \)とすると、$$I =\frac{1}{R_p} E \;\;\;\;\;\; \frac{1}{R_p} = \frac{1}{R_1} + \frac{1}{R_2}$$である。この場合、$$\frac{1}{R_p} = \frac{R_1 + R_2}{R_1 R_2} \\ R_p = \frac{R_1 R_2}{R_1 + R_2}$$となる。
また、$$E = R_p I = \frac{R_1 R_2}{R_1 + R_2} I$$ なので、$$I_1 = \frac{E}{R_1} =\frac{\frac{R_1 R_2}{R_1 + R_2} I }{R_1} =\frac{R_2}{R_1 + R_2} I$$となる。同様にして、$$I_2 = \frac{R_1}{R_1 + R_2}$$となる。これを分流の式という。
抵抗の並列接続
\(n\)個の抵抗を並列接続したときの合成抵抗は、$$\frac{1}{R_p} =\frac{1}{R_1} +\frac{1}{R_2} + \cdots + \frac{1}{R_n}$$となる。また、\(R = R_1 = R_2 = \cdots \)を\(n\)個 並列接続した場合の合成抵抗は、$$\frac{1}{R_p} = n\times \frac{1}{R}$$ $$R_p =\frac{R}{n} $$となる。
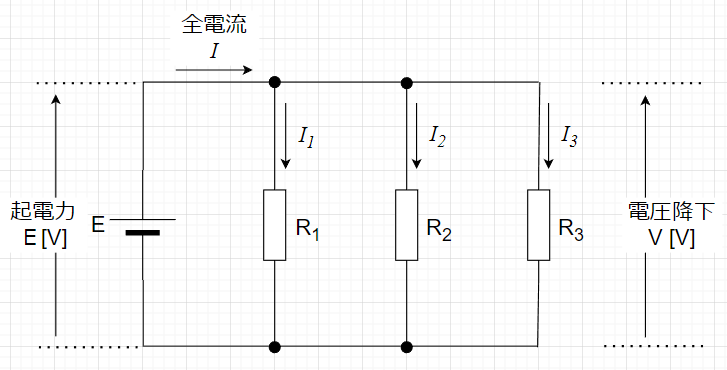
図「抵抗3個の並列接続」で考える。\(E\)は起電力\(E \;[V]\)の電源、\(R_1 \;,\; R_2 \;,\; R_3\)が抵抗である。
並列接続なので、同じ電圧\(E\)が抵抗\(R_1 \;,\; R_2 \;,\;R_3\)に印可される。オームの法則により、抵抗\(R_1\)に流れる電流は、\(I_1 =\frac{E}{R_1} \)、抵抗\(R_2\)に流れる電流は、\(I_2= \frac{E}{R_2}\) 、抵抗\(R_3\)に流れる電流は、\(I_3= \frac{E}{R_3}\) となる。また、各抵抗に流れる電流の合計が全電流であり、\(I = I_1 + I_2 + I_3\)となる。$$I = I_1 + I_2 + I_3= \frac{E}{R_1} + \frac{E}{R_2} +\frac{E}{R_3} \\ = \left(\frac{1}{R_1} + \frac{1}{R_2} +\frac{1}{R_3}\right)E$$並列接続の合成抵抗を\(R_p \)とすると、$$I =\frac{1}{R_p} E \;\;\;\;\;\; \frac{1}{R_p} = \frac{1}{R_1} + \frac{1}{R_2} + \frac{1}{R_3}$$である。この場合、$$\frac{1}{R_p} = \frac{R_1 R_2+ R_2 R_3 +R_3 R_1}{R_1 R_2 R_3} \\ R_p = \frac{R_1 R_2 R_3}{R_1 R_2 + R_2 R_3 + R_3 R_1}$$となる。


“3. 抵抗の直列接続、並列接続” に対して4件のコメントがあります。
コメントは受け付けていません。