20. 正弦波交流の複素数表示
正弦波交流電流、電流やインピーダンスなどは、複素数によって表すことができる。特に、オイラーの公式を使った三角関数表示、指数関数表示により、回路解析の計算を効率よく行うことができる。
複素数表示に必要な事項
1)電気工学において、虚数単位は、\(j = \sqrt{-1}\)が用いられる。\(j^2 = -1\)である。
2)複素数\(Z\)は、実数\(a,b\)を用いて\(Z=a+jb\)と表される。\(a\)は複素数の実部、\(b\)は複素数の虚部とよばれ、\(a = \mathrm{Re} \{Z\} \;\;\;\;\ b = \mathrm{Im} \{Z\}\)と表すこともある。
3)虚部の符号だけが異なる2つの複素数\(a+jb , a-jb\)は互いに共役な複素数という(共役複素数)。その積は実数となる。$$(a+jb)(a-jb)=a^2 + b^2$$
複素平面(ガウス平面)
複素数は、複素平面(図「複素平面」参照)上の点\(Z\)で表される。複素平面の横軸は実軸(\(Re\)で表記)、縦軸は虚軸(\(Im\)で表記)という。\(Z\)は$$Z=a+jb$$と表され、複素数の絶対値(大きさ)は、原点からの距離で表され、$$|Z|=|a+jb|=\sqrt{a^2 + b^2}$$である。また、共役な複素数は、\(\bar{Z}=a-jb\)であり、$$Z\cdot \bar{Z} = (a+jb)(a-jb) \\= a^2 + b^2 = (|Z|)^2$$となる。
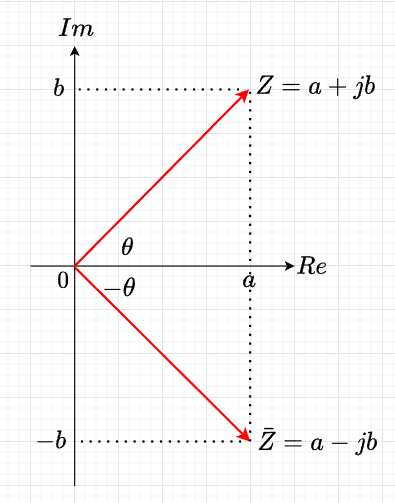
また、\(Z\)と実軸\(Re\)とのなす角を\(\theta\)とすると、$$\cos \theta = \frac{a}{\sqrt{a^2 + b^2}} ,\;\;\;\;\; \sin \theta = \frac{b}{\sqrt{a^2 + b^2}} ,\;\;\;\;\; \tan \theta = \frac{b}{a}$$となる。この\(\theta\)を偏角という。\(\theta\)は、$$\theta = \tan^{-1} \frac{b}{a}, \;\;\;\; \mathrm{arg} \;Z,\;\;\;\;\; \angle{Z}$$等で表される。偏角は、\(n\)を整数として\(\theta = \theta_0 + 2n\pi \;\;\;\; (-\pi \lt \theta_0 \le \pi )\)となり、\(\theta_0\)は偏角の主値である。
\(a = |Z| \cos \theta , \;\;\;\; b=|Z| \sin \theta \)と書けるので、$$a + jb =|Z|(\cos \theta +j \sin \theta)$$である。
複素数の加減乗除
2つの複素数を\(Z_1 = a_1 + j b_1 , \;\;\;\; Z_2 =a_2 + jb_2 \)とする。\(Z_1\)と\(Z_2\)の和\(Z\)は、それぞれの実部の和と虚部の和になるので、$$Z = Z_1 + Z_2 = (a_1 + j b_1) + (a_2 + j b_2) = (a_1 + a_2) + j(b_1 + b_2)$$である。このとき、$$|Z|=\sqrt{(a_1 + a_2)^2 + (b_1 + b_2)^2} , \;\;\;\; \theta = \tan^{-1} \frac{b_1 + b_2}{a_1 + a_2}$$である。
\(Z_1\)と\(Z_2\)の積\(Y\)は、$$Y = (a_1 + j b_1) \cdot (a_2 + j b_2) =(a_1 a_2 - b_1 b_2) + j (a_1 b_2 + a_2 b_1)$$である。このとき、$$|Y| = \sqrt{ (a_1 a_2 - b_1 b_2) ^2 + (a_1 b_2 + a_2 b_1)^2} = \sqrt{{a_1}^2 + {b_1}^2} \sqrt{{a_2}^2 +{b_2}^2} \\ \theta = \tan^{-1} \frac{a_1 b_2 + a_2 b_1}{a_1 a_2 - b_1 b_2} = \tan^{-1} \frac{\frac{b_1}{a_1} + \frac{b_2}{a_2}}{1 - \frac{b_1}{a_1} \frac{b_2}{a_2}} = \tan^{-1} \frac{b_1}{a_1} + \tan^{-1} \frac{b_2}{a_2}$$すなわち、\(Z_1 , Z_2\)の積の大きさは、\(Z_1 = \sqrt{{a_1}^2 + {b_1}^2}\)と\(Z_2 = \sqrt{{a_2}^2 + {b_2}^2}\)の積であり、その偏角は、\(Z_1\)の偏角\(\tan^{-1} \frac{b_1}{a_1}\)と\(Z_2\)の偏角\(\tan^{-1} \frac{b_2}{a_2}\)の和となる。
\(Z_1\)を\(Z_2\)で割るとその商\(X\)は、$$X = \frac{a_1 + j b_1}{a_2 + j b_2} = \frac{a_1 + j b_1}{a_2 + j b_2} \cdot \frac{a_2 - j b_2}{a_2 - j b_2} = \frac{a_1 a_2 + b_1 b_2}{{a_2}^2 + {b_2}^2} + j \frac{a_2 b_1 - a_1 b_2}{{a_2}^2 + {b_2}^2} $$である。このとき、$$|X| = \sqrt{\left(\frac{a_1 a_2 + b_1 b_2}{{a_2}^2 + {b_2}^2} \right)^2 + \left( \frac{a_2 b_1 - a_1 b_2}{{a_2}^2 + {b_2}^2}\right)^2} = \frac{\sqrt{{a_1}^2 + {b_1}^2}}{\sqrt{{a_2}^2 + {b_2}^2}} \\ \theta = \tan^{-1} \frac{a_2 b_1 - a_1 b_2}{a_1 a_2 + b_1 b_2} = \tan^{-1} \frac{ \frac{b_1}{a_1} -\frac{b_2}{a_2}}{1 + \frac{b_1}{a_1} \frac{b_2}{a_2}} = \tan^{-1} \frac{b_1}{a_1} - \tan^{-1} \frac{b_2}{a_2}$$すなわち、\(Z_1 , Z_2\)の商の大きさは、\(Z_1 = \sqrt{{a_1}^2 + {b_1}^2}\)を\(Z_2 = \sqrt{{a_2}^2 + {b_2}^2}\)で除した値であり、その偏角は、\(Z_1\)の偏角\(\tan^{-1} \frac{b_1}{a_1}\)と\(Z_2\)の偏角\(\tan^{-1} \frac{b_2}{a_2}\)の差となる。
極座標表示
複素数は、\(Z = a + jb =|Z|(\cos \theta +j \sin \theta)\)と表す。オイラーの公式より、\(\cos\theta + j \sin \theta = e^{j \theta}\)なので、$$Z=|Z|(\cos \theta + j \sin \theta) = |Z|e^{j \theta}$$である。2つの複素数を\(Z_1 = a_1 + j b_1=|Z_1|e^{j \theta_1} , \;\;\; Z_2 =a_2 + jb_2 = |Z_2|e^{j \theta_2} \)とする。
このとき、積は、$$Z_1 Z_2 = |Z_1|e^{j \theta_1}\times |Z_2|e^{j \theta_2} = |Z_1||Z_2|e^{j(\theta_1 + \theta_2)}$$である。
また、\(Z_k =a_k + j b_k = |Z_k|e^{j\theta}\)とすれば、この\(n\)乗は、$$Z_k^n = (|Z_k| e^{j\theta})^n = |Z_k|^n e^{j n \theta} =|Z_k|^n (\cos n \theta + j \sin n \theta) \;\;\;\; nは整数$$となる。
同様に、商は、$$\frac{Z_1}{Z_2} = \frac{|Z_1|e^{j \theta_1}}{|Z_2|e^{j \theta_2}} = \frac{|Z_1|}{|Z_2|}e^{j (\theta_1 - \theta_2)}$$である。
交流の複素数表示
実効値\(I_1\)、振幅\(I_{m_1}= \sqrt{2} I_1\)、角周波数\(\omega\)、位相\(\theta_1\)の交流電流を$$i_1 = I_{m_1} \sin(\omega t + \theta_1) \; [A]$$実効値\(I_2\)、振幅\(I_{m_2}= \sqrt{2} I_2\)、角周波数\(\omega\)、位相\(\theta_2\)の交流電流を$$i_2 = I_{m_2} \sin(\omega t + \theta_2) \; [A]$$とする。このとき、$$i = i_1 + i_2 = I_{m_1} \sin(\omega t + \theta_1) + I_{m_2} \sin(\omega t + \theta_2) \\= I_{m_1} \sin\omega t \cos \theta_1 + I_{m_1} \cos \omega t \sin \theta_1 + I_{m_2} \sin \omega t \cos \theta_2 + I_{m_2} \cos\omega t \sin \theta_2 \\ =(I_{m_1} \cos \theta_1 + I_{m_2} \cos \theta_2)\sin \omega t + (I_{m_1} \sin \theta_1 + I_{m_2} \sin \theta_2)\cos \omega t \\ = \sqrt{(I_{m_1} \cos \theta_1 + I_{m_2} \cos \theta_2)^2 + (I_{m_1} \sin \theta_1 + I_{m_2} \sin \theta_2)^2} \times (\sin \omega t \cos \theta_0 + \cos \omega t \sin \theta_0) \\ = \sqrt{{I_{m_1}}^2 + {I_{m_2}}^2 + 2 I_{m_1}I_{m_2} \cos(\theta_1 -\theta_0)} \times \sin(\omega t + \theta_0) \; [A] \\ \theta_0 = \tan^{-1}\frac{I_{m_1} \sin \theta_1 + I_{m_2} \sin \theta_2}{I_{m_1} \cos \theta_1 + I_{m_2} \cos \theta_2} \; [\mathrm{rad}] $$ となるので、根号の部分を\(I_m\)とおけば、結局、$$i = i_1 + i_2 = I_m \sin(\omega t + \theta_0) \; [A]$$なので、\(i_1,i_2\)とは振幅と位相が異なる一つの正弦波交流電流となる。
ここで、\(i_1,i_2,i\)を複素数表示すると、$$i_1 = I_{m_1}e^{j(\omega t + \theta_1)} = I_{m_1}\left\{ \cos (\omega t + \theta_1) + j \sin(\omega t + \theta_1)\right\} \\ i_2 = I_{m_2}e^{j(\omega t + \theta_2)} = I_{m_2}\left\{ \cos (\omega t + \theta_2) + j \sin(\omega t + \theta_2)\right\} \\ i = I_{m}e^{j(\omega t + \theta)} = I_{m}\left\{ \cos (\omega t + \theta) + j \sin(\omega t + \theta)\right\}$$となる。ここで、$$i_1 + i_2 = \left\{ I_{m_1} \cos(\omega t + \theta_1) + I_{m_2} \cos(\omega t + \theta_2) \right\} + j \left\{I_{m_1}\sin(\omega t + \theta_1) + I_{m_2} \sin(\omega t + \theta_2)\right\} \\=I_m \left\{ \cos(\omega t + \theta) + j\sin(\omega t + \theta)\right\} = i$$が成り立つ。このことは、交流電流の合成が、複素数表示された電流の合成の虚部に等しくなることを示している。従って、交流電流は、加算まで含めて複素数表示で取り扱うことができる。
以上のことは、交流電圧についても同様である。
交流の合成【例】
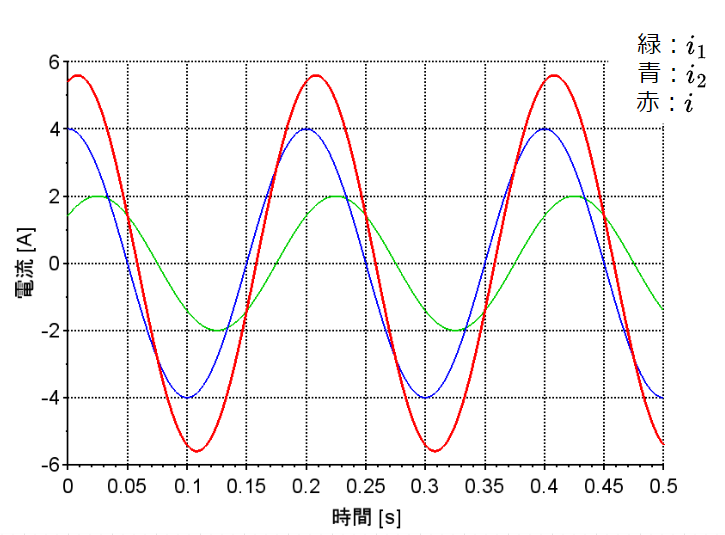
交流電流で、\(i_1\)を振幅\(2 \;[A]\)、周波数\(5\;[Hz]\)、位相\(\frac{\pi}{4}\)、\(i_2\)を振幅\(4 \;[A]\)、周波数\(5\;[Hz]\)、位相\(\frac{\pi}{2}\)として、\(i=i_1 + i_2\)を求める。
$$i_1 = 2 \sin\left(10\pi + \frac{\pi}{4}\right) \;\;\; i_2 = 4 \sin\left(10\pi + \frac{\pi}{2}\right) \\ i = i_1 + i_2$$として計算すると、図「交流の加算」のようになる。グラフ作成には、Scilabを使用した。