2. 複素数の演算
2次方程式の解
2次方程式の解の公式は暗記するのではなく、平方完成から求められることを理解することが大切である。以下は解の公式導出の概要であるので厳密な議論は省略している。
\(ax^2+bx+c=0\) より、\(a\not=0\)として、両辺を\(a\)で割って \(x^2+\frac{b}{a}x+\frac{c}{a}=0\) となる。 ただし、\(a,b,c\)は実数とする。
従って、\( (x+\frac{b}{2a})^2-(\frac{b}{2a})^2+\frac{c}{a}=0 \) \( (x+\frac{b}{2a})^2=(\frac{b}{2a})^2-\frac{c}{a} \)
整理すると \( (x+\frac{b}{2a})^2=(\frac{b^2-4ac}{4a^2}) \) よって、\( x+\frac{b}{2a}=\pm\frac{\sqrt{b^2-4ac}}{2a} \)
以上より、$$ x=\frac{-b \pm \sqrt{b^2-4ac}}{2a} $$
なお、\( D=b^2-4ac<0 \)のときは、解は複素数となり、必ず共役複素数となる。
複素数の基本的な演算
複素数の演算では、複素平面(ガウス平面)を念頭に置いて考えると良い。また、オイラーの公式は良く使うので、成り立ちを含めて理解しておくと様々な場面で役に立つ。
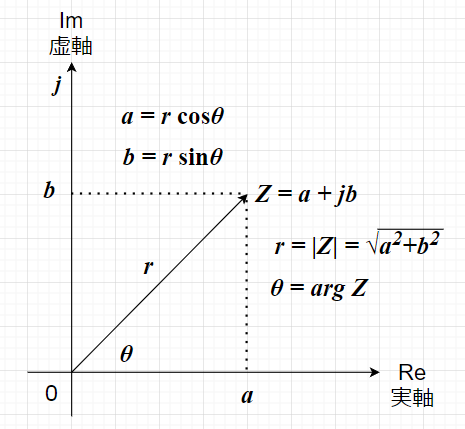
$$ z=a+jb $$ 図より、
\( | z |=r=\sqrt{a^2+b^2} \) , \(a=r\cos\theta\) , \(b=r\sin\theta\)
\( z=a+jb=r\cos\theta+jr\sin\theta\)
\(=r(\cos\theta+j\sin\theta)=re^{j\theta} \)
\( \tan\theta \) → \(\theta=arg(z)=\tan^{-1}(\frac{b}{a})\)
\(z=a-jb\) が共役複素数
(実部が等しくて虚部の符号が反対)
\(z+\bar{z}=(a+jb)+(a-jb)=2a\) , \(z \cdot \bar{z}=(a+jb) \cdot (a-jb)=a^2+b^2=r^2\)
\(\frac{c+jd}{a+jb}=\frac{r_1 e^{j\theta_1}}{r_2 e^{j\theta_2} }=\frac{r_1}{r_2}e^{j(\theta_1-\theta_2)} \) , \(\theta_1-\theta_2=\tan^{-1}\frac{d}{c}-\tan^{-1}\frac{b}{a}\)
\(\frac{(c+jd)(a-jb)}{(a+jb)(a-jb)}=\frac{(ac+bd)+j(ad-bc)}{a^2+b^2}\) , \(r=\sqrt{(\frac{ac+bd}{a^2+b^2})^2+(\frac{ad-bc}
{a^2+b^2})^2}=\frac{\sqrt{c^2+d^2}}{\sqrt{a^2+b^2}}=\frac{r_1}{r_2}\)
\(\theta=\theta_1-\theta_2=\tan^{-1}(\frac{ad-bc}{ac+bd})\)
※制御工学や電気工学では、一般に虚数単位は\(j\)を使う

