9. 離散時間システムの基本構成
離散時間システムを記述する式(1)に示す差分方程式から分かるように、入力\(x(n)\)に対する出力\(y(n)\)の計算は、積和演算を実行すればよい。$$y(n) = \sum_{k=0}^{M} a_k x(n-k) - \sum_{k=1}^{N} b_k y(n-k) \;\cdots\cdots(1)$$一般に離散時間システムは、図1に示す加算器、乗算器、遅延器の3つの基本要素としてシステムを構成することができる。実際の演算は、多くの場合、2進数のディジタル演算で実行される。
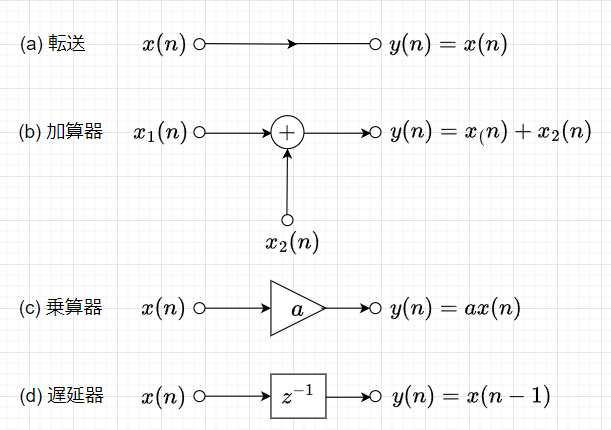
(1) 加算器:2つの入力\(x_1(n),\; x_2(n)\)に対して、\(y(n) = x_1(n) + x_2(n)\)あるいは、\(y(n) = x_1(n) -x_2(n)\)を出力する。
(2)乗算器:入力\(x(n)\)にある定数\(a\)を乗じた\(y(n) = a x(n)\)を出力する。
(3)遅延器:入力\(x(n)\)に対して単位時間の遅延を与えた\(y(n) = x(n-1)\)を出力する。単位時間遅延は\(z^{-1}\)で表す。
システムの例
1次系のシステム構成を考える。差分方程式と伝達関数は、$$y(n) = a_0 x(n) + a_1 x(n-1) - b_1 y(n-1) \\Y(z) = a_0 X(z) + a_1 X(z) z^{-1} - b_1 Y(z) z^{-1} \\ H(z)= \frac{a_0 + a_1 z^{-1}}{1 + b_1 z^{-1}}$$とする。このとき、システム構成は、差分方程式の演算等を図1の要素に置き換えて描くことで、図2のように表せる。図2の(1)の部分と(2)の部分は入れ換えても入出力関係は変わらないので、図3上図のように書き換えることができる。さらに、遅延器部分は1つにまとめることができるので、図3下図のように簡略化したシステム構成が得られる。遅延器を1つ省略できるということは、ディジタル回路では記憶素子を減らせることになり、プログラミングではスタックなどの記憶領域を減らせることになる。
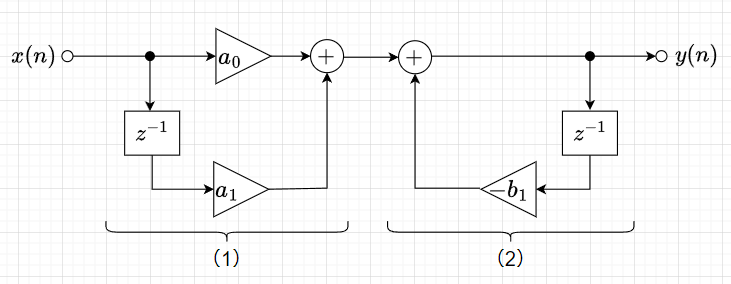
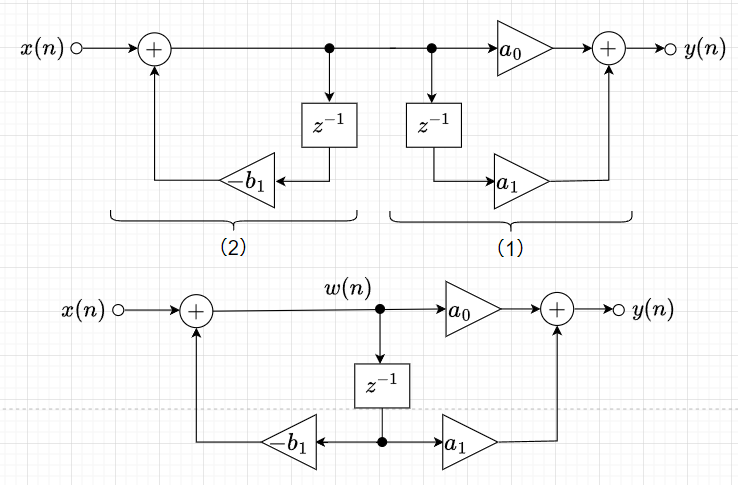
図3の伝達関数を求める。図3の差分方程式は、$$x(n) =w(n) - b_1 w(n-1) \\ y(n) = a_0 w(n) +a_1 w(n-1) $$と表せる。これを\(Z\)変換すると、$$X(z) = W(z) + b_1 W(z) z^{-1} \\ Y(z) = a_0 W(z) + a_1 W(z) z^{-1} \\ H(z) = \frac{Y(z)}{X(z)} = \frac{a_0 + a_1 z^{-1}}{1 + b_1 z^{-1}}$$ となり、図3のシステムが図2のシステムと同じ伝達関数を持つことが分かる。
高次システムの構成
式(1)の差分方程式で表される離散時間システムの伝達関数は、$$H(z) = \frac{a_0 + a_1 z^{-1} + a_2 z^{-2} + \cdots + a_M z^{-M}}{1 + b_1 z^{-1} + b_2 z^{-2} + \cdots + b_N z^{-N}} \cdots (2)$$となる。この分母・分子の多項式を因数分解すれば、1次系と2次系の積の形で高次のシステムを構成することができる。つまり、$$H(z) = a_0 \cdot H_1(z) \cdot H_2(z) \cdots H_{i}(z)$$となる。ここで、\(a_0\)は定数、\(i\)は正の整数である。各\(H_i(z)\)は、1次または2次の伝達関数である。図4のように描け、このような構成を縦続接続という。3次系のシステムであれば、1次系と2次系を、4次系であれば、2次系を2組というように、縦続接続することで、高次のシステムを実現できる。
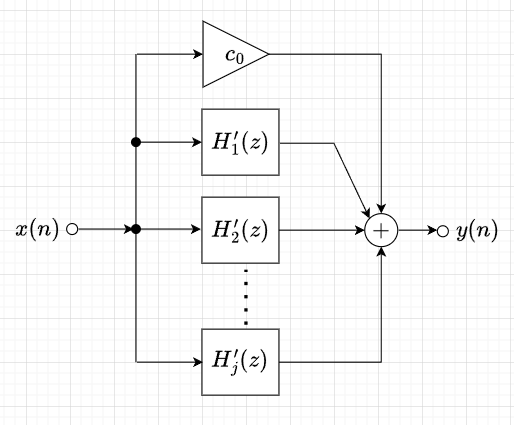
また、式(2)は次式のように表すこともできる。$$H(z) = c_0 + H_1'(z) + H_2'(z) + \cdots + H_j'(z)$$ここで、\(c_0\)は定数、\(j\)は正の整数、各\(H_j(z)\)は、1次または2次の伝達関数である。図5のように描け、このような構成を並列接続という。