5. 連続時間信号の標本化
連続時間信号の標本化とは、時間軸上で連続的に変化する信号を、一定間隔で値を取り出すことで離散的な信号に変換する処理である。これは、アナログ信号をディジタル信号に変換する最初のステップであり、信号処理やコンピュータでの処理に必要不可欠な技術である。特に標本化を行うには、標本化定理と呼ばれる重要な理論に基づいて、サンプリング周波数と呼ばれる適切な間隔で値を取り出す必要がある。
サンプル値信号
連続時間信号\(x(t)\)は標本化によって離散時間信号として取り出される。この取り出す時間間隔\(T\)をサンプリング周期、また、\(f_s = 1/T\)をサンプリング周波数という。
信号\(x(t)\)が理想サンプラを通過すると出力はサンプル値信号\(x_s(t)\)となり、これは\(x(t)\)と単位インパルス列\(\delta_T(t)\)の積となる。つまり、\(x_s(t) = x(t) \delta_T(t)\) である。\(\delta(t)\)の性質から\(x_s(t)\)は、$$x_s(t) = x(t) \sum_{n=-\infty}^{\infty} \delta(t-nT) = \sum_{n=-\infty}^{\infty} x(nT) \delta (t - nT)$$と表せる。\(x_s(t)\)は、サンプル点において\(x(t)\)に等しいといえる。サンプル値信号\(x_s(t)\)の信号系列\(\{x(nT)\}\)からもとの連続時間信号\(x(t)\)へ復元できるためには、標本化定理を満たす必要がある。
標本化定理
標本化定理は、「連続時間信号\(x(t)\)が\(f_c\;[Hz]\)以上の周波数成分を含まない、つまり、最高周波数を\(f_c \;[Hz]\)とすれば、\(2f_c \; [Hz]\)より高い周波数のサンプリング周波数\(f_s\)、または、\(T_s =1/(2f_c) \; [s]\)未満のサンプリング周期で信号\(x(t)\)を標本化すれば、その標本化系列\(\{x(n)\}\)から元の信号\(x(t)\)を完全に復元できる」ことをいう。\(f_s > 2f_c \;\;\;\; T_s < 1/(2 f_c)\)である。
標本化定理の導出
連続時間信号\(x(t)\)は、最高角周波数\(\omega_c = 2 \pi f_c\)で帯域制限されている。\(x(t)\)の周波数スペクトルを\(X(\omega)\)とする。サンプル値信号を\(x_s(t)\)、その周波数スペクトルを\(X_s(\omega)\)とする。\(x_s(t)\)の\(X_s(\omega)\)をフーリエ変換の定義より求める。$$X_s(\omega) = \int_{-\infty}^{\infty} x_s(t) e^{-j \omega t}dt = \int_{-\infty}^{\infty} \left\{ \sum_{n = -\infty}^{\infty} x(nT) \delta(t - nT) \right\}e^{-j\omega t}dt \\ = \sum_{n= -\infty}^{\infty} x(nT) \int_{-\infty}^{\infty} \delta(t - nT)e^{-j\omega t}dt = \sum_{n=-\infty}^{\infty} x(nT) e^{-j n \omega T}\;\; \cdots (1)$$( \(\int_{-\infty}^{\infty} \delta(t - t_0)x(t)dt = x(t_0)\)を使った)
式(1)は、\(x_s(t)\)のフーリエ変換であると同時に、フーリエ係数を\(x(nT)\)として\(X_s(\omega)\)がフーリエ級数に展開できることを示している。すなわち、サンプル値信号\(x_s(t)\)のフーリエ変換を求めると\(X_s(\omega)\)は角周波数\(\omega\)の周期関数になることがわかる。\(k\)を任意の整数として、\(X_s(\omega) = X_s(\omega + k \omega_s)\)であり、\(X_s(\omega)\)の周期はサンプリング角周波数\(\omega_s\)に等しい。
単位インパルス列のフーリエ変換
単位インパルス列\(\delta_T(t)\)は、$$\delta_T(t) = \sum_{n=-\infty}^{\infty} \delta(t - nT) \\ c_n = \frac{1}{T} \int_{-T/2}^{T/2} \delta_{T}(t) e^{-j n \omega_s t}dt = \frac{1}{T} \int_{-T/2}^{T/2} \delta(t) e^{-j n \omega_s t}dt = \left[\frac{1}{T} e^{-j n \omega_s t} \right]_{t=0} = \frac{1}{T}$$よって、$$\delta_T(t) = \frac{1}{T}\sum_{n=-\infty}^{\infty} e^{j n \omega_s t} = \frac{1}{T} + \sum_{n=1}^{\infty} \frac{2}{T} \cos n \omega_s t$$ となる。\(e^{j \omega_0 t} \Leftrightarrow 2 \pi \delta(\omega - \omega_0)\)なので、$$\mathcal{F} \{ \delta_T(t)\} = \frac{1}{T} \sum_{n=-\infty}^{\infty} 2 \pi \delta( \omega - n \omega_s) = \omega_s \sum_{n=-\infty}^{\infty} \delta( \omega - n \omega_s)$$となる。
単位インパルス列\(\delta_T(t)\)のフーリエ変換は、$$\mathcal{F}\{\delta_T(t)\} = \omega_s \sum_{n=-\infty}^{\infty} \delta( \omega - n \omega_s)$$であり、時間領域の積のフーリエ変換は、周波数領域で畳み込み積分になる。\(x_s(t)\)は、\(x(t)\)と\(\delta_T(t)\)の積で与えられるから、\(x_s(t)\)のフーリエ変換\(X_s(\omega)\)は、$$X_s(\omega) = \frac{1}{2 \pi} \left[ X(\omega) \ast \omega_s \sum_{n= -\infty}^{\infty} \delta( \omega - n \omega_s) \right] = \frac{1}{T} \left[ X(\omega) \ast \sum_{n= -\infty}^{\infty} \delta( \omega - n \omega_s) \right] \\ = \frac{1}{T} \sum_{n = -\infty}^{\infty} X(\omega) \ast \delta( \omega - n \omega_s) = \frac{1}{T} \sum_{n=-\infty}^{\infty} X( \omega - n \omega_s)\;\; \cdots (2)$$となる。(\(x(t) \ast \delta(t - t_0) = x(t - t_0)\)の関係を使った)
式(2)は、図1(a)に示す連続時間信号\(x(t)\)の周波数スペクトル\(X(\omega)\)を図1(b)とすると、\(X(\omega)\)に\(1/T\)を掛けてサンプリング角周波数\(\omega_s\)ごとに並べたものを全て加算したものが図1(f)の\(X_s(\omega)\)に等しくなることを示している。ここで、\(x(t)\)の周波数スペクトル\(X(\omega)\)の最高角周波数を\(\omega_c\)としたとき、\(\omega_s > 2\omega_c\)(\(f_s > 2 f_c\)) であれば、\(\omega_s\)で繰り返す\(X_s(\omega)\)の周波数スペクトルは、重なり合うことは無い。従って、$$X_s(\omega) = \frac{1}{T} X(\omega) \;\;\;\; (-\omega_c \leq \omega \leq \omega_c)$$となり、\(X(\omega)\)と\(X_s(\omega)\)の周波数スペクトルが同じ特性を示すので、サンプル値信号\(x_s(t)\)から\(x(t)\)が復元可能と言える。
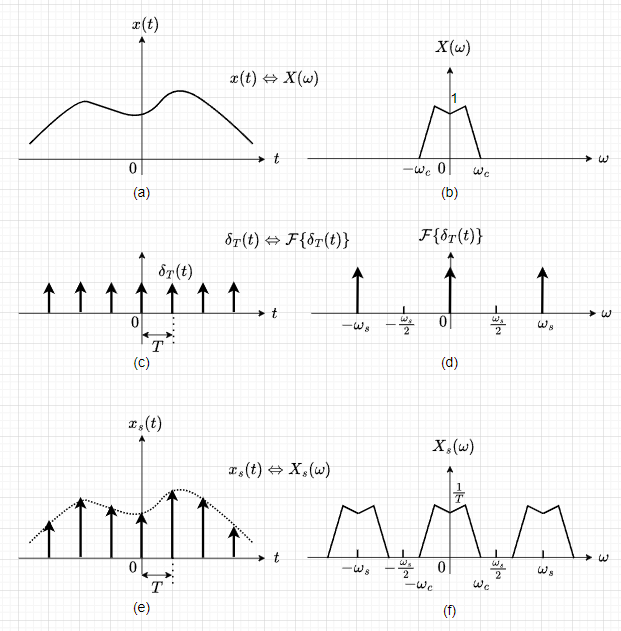
サンプル値信号\(x_s(t)\)の系列\(\{x(nT)\}\)から\(x(t)\)を復元することを考える。
\(-\omega_s /2 < \omega < \omega_s/2\)(\(-\pi/T < \omega < \pi/T\))の範囲で、$$X_s(\omega) = \frac{1}{T}X(\omega)$$なので、連続時間信号\(x(t)\)のフーリエ変換は、$$x(t) = \frac{1}{2 \pi} \int_{-\pi/T}^{\pi/T} X(\omega) e^{j \omega t} d\omega \\ = \frac{1}{2 \pi} \int_{-\pi/T}^{\pi/T} TX_s(\omega) e^{j \omega t} d\omega $$と書ける。
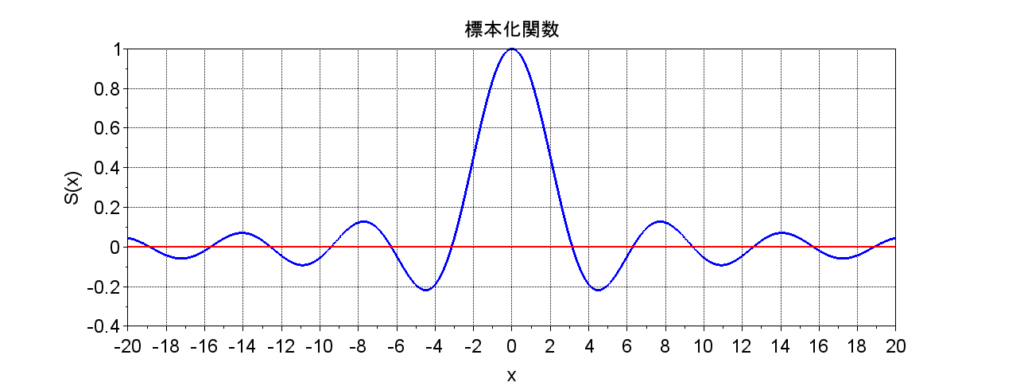
\(x=\pm n\pi \;\;\;(n=1,2,3,\cdots)\)
において\(S(x) = 0 \)
式(1)を代入すると、$$x(t) = \frac{T}{2 \pi} \int_{-\pi/T}^{\pi/T}\left\{ \sum_{n=-\infty}^{\infty} x(n T) e^{-j n \omega T} \right\} e^{j \omega t} d\omega \\ = \sum_{n=-\infty}^{\infty} x(nT) \left[ \frac{T}{2 \pi} \int_{- \pi/T}^{\pi/T} e^{j \omega(t - nT)} d\omega\right]$$となる。積分部分は、$$\int_{- \pi/T}^{\pi/T} e^{j \omega(t - nT)} d\omega = \frac{1}{j (t - nT)} \left[e^{j \omega(t - nT)} \right]_{-\pi/T}^{\pi/T} \\ = \frac{1}{j (t - nT)} \left(e^{j (t - nT) \pi /T} - e^{-j (t - nT)\pi /T} \right) \\= \frac{2}{t - nT} \sin(t -nT)\pi /T$$ なので、$$x(t) =\sum_{n = -\infty}^{\infty} x(nT) \frac{\sin \pi(t - nT)/T}{\pi (t - nT)/T} = \sum_{n=-\infty}^{\infty} x(nT) \frac{\sin \omega_c(t - nt)}{\omega_c (t - nT)}\;\; \cdots (3)$$となる。$$S(x)=\frac{\sin x}{x}$$を標本化関数とすると、式(3)は、標本化関数\(S(x)\)にサンプル値\(x(nT)\)を掛けて、\(n= -\infty \sim \infty\)にわたって得られる波形を全て加えることで連続時間信号\(x(t)\)が復元できる、と解釈できる。サンプリング間隔の最大間隔\(T = 1/(2 f_c)\)をナイキスト間隔という。また、\(2f_c\)をナイキスト周波数という。サンプリング周波数\(f_s\)はナイキスト周波数より高くなければならない。(元の信号を復元するための適正なサンプリング間隔はナイキスト間隔未満ということになる。)
図2に標本化関数を示す。この標本化関数で\(S(x)=0\)になる\(x\)は、\(\pm n\pi\ \;\; (n=1,2,3,\cdots)\)である。
エイリアシング
エイリアシングとは、本来異なる周波数の信号が、サンプリングによって区別できなくなり、偽の信号が発生してしまう現象である。「折り返し歪み」とも呼ばれる。
連続時間信号は時間軸上で滑らかに変化しているが、サンプリングによって特定の時点での値しか取得できない。サンプリング周波数が信号の最高周波数の2倍より高くなければ、つまり標本化定理を満たしていないと、エイリアシングが発生する。
図3により、エイリアシングの発生を周波数スペクトルで考える。図3(a)が連続時間信号\(x(t)\)の周波数スペクトル\(X(\omega)\)である。\(x(t)\)の最高角周波数を\(\omega_c\)とする。図3(b)は、\(x(t)\)をサンプリング角周波数\(\omega_s = 2\omega_c\)でサンプリングした信号\(x_s(t)\)の周波数スペクトル\(X_s(\omega)\)である。この場合、周波数スペクトルは\(\omega(s)\)で繰り返し、\(\frac{\omega_s}{2} = \omega_c\)の点で周波数スペクトルが一致する。(この点を除けば、各周波数スペクトルは分離している。)一方、図3(c)のように\(\omega_s < 2\omega_c\)でサンプリングした場合、各周波数スペクトルが重なってしまい、赤い線で示した偽のスペクトルが発生してしまう。つまり、\(x_s(t)\)から、\(x(t)\)が復元できなくなり、エイリアシング(折り返し歪み)が生じることになる。
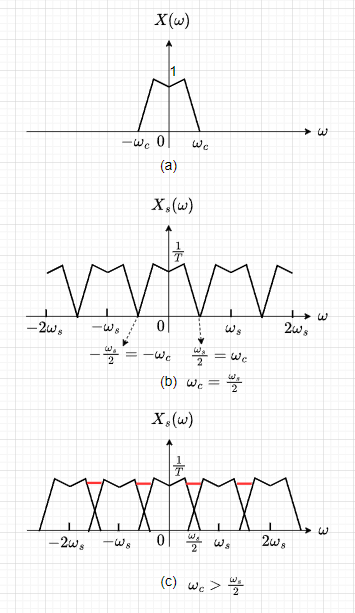
エイリアシングを防ぐ方法は、主に以下の2点がある。
1)サンプリング周波数を高くする:サンプリング周波数を信号の最高周波数の2倍より高くすることで、エイリアシングを防ぐことができる。
2)アンチエイリアシングフィルタを使用する:アンチエイリアシングフィルタにより、サンプリングする前の元の信号で、エイリアシングの原因となる高周波成分をカットする。


“5. 連続時間信号の標本化” に対して1件のコメントがあります。
コメントは受け付けていません。