2. フーリエ級数
フーリエ級数とは、周期関数を三角関数の和で表す数学的な方法である。ここで、周期関数とは、一定の周期で繰り返す関数を指す。工学的には、フーリエ級数は複雑な形状の周期信号を、単純な三角関数の重ね合わせで表現することができる。これは、複雑な信号を理解しやすくするために有効な手法である。
周期信号
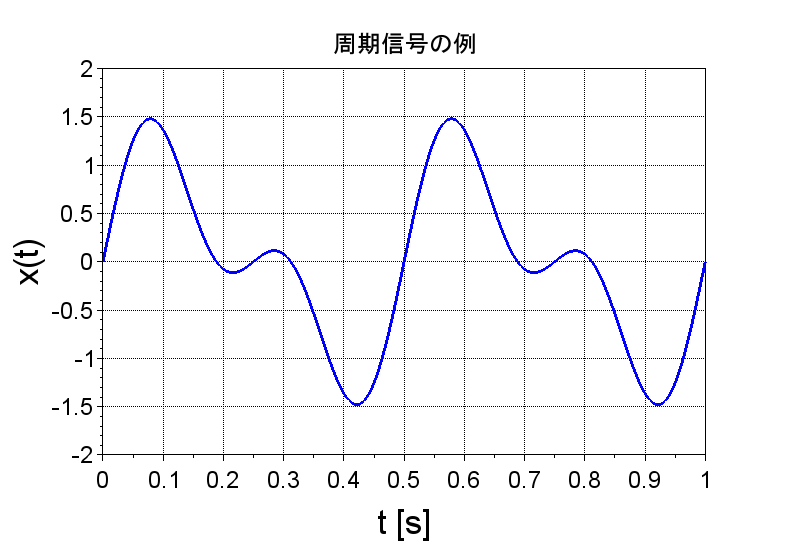
周期信号とは、すべての時刻\(t\)に対して、$$x(t) = x(t+nT_0)$$の関係が成立する信号と定義される。ここで、\(T_0\)は周期、\(n\)は整数である。図1に周期信号の例を示す。周期\(T_0=0.5 \;s\)の周期信号となっている。
フーリエ級数
信号\(x(t)\)が周期\(T_0\)の周期信号であれば、$$x(t) = \frac{1}{2}a_0 + a_1\cos\omega_0 t + a_2 \cos 2\omega_0 t + \cdots + b_1 \sin \omega_0 t + b_2 \sin2 \omega_0 t + \cdots \\ = \frac{1}{2}a_0 + \sum_{n=1}^{\infty} (a_n \cos n \omega_0 t + b_n \sin n \omega_0 t) \cdots \cdots (1)$$となる。この式を三角関数のフーリエ級数という。角周波数\(\omega_n = n \omega_0\)の正弦波成分を\(x(t)\)の\(n\)次高調波という。角周波数\(\omega_0\)の成分は、\(x(t)\)と同じ周期を持つ基本周波数成分である。\(\omega_0 = 2 \pi f_0 = 2 \pi /T_0\)を基本角周波数、\(f_0\)を基本周波数という。式(1)の\(a_n,\; b_n\)をフーリエ係数という。\(a_0/2\)は信号\(x(t)\)の平均値で、直流成分を表している。フーリエ係数\(a_n,\; b_n\)は、$$a_n = \frac{2}{T_0}\int_{-T_0/2}^{T_0/2} x(t) \cos n \omega_0 t dt, \;\;\;\;\; n= 0,1,2, \cdots \cdots \\ b_n = \frac{2}{T_0}\int_{-T_0/2}^{T_0/2} x(t) \sin n \omega_0 t dt, \;\;\;\;\; n= 1,2, \cdots \cdots$$で求まる。
フーリエ級数の例
方形波のフーリエ級数
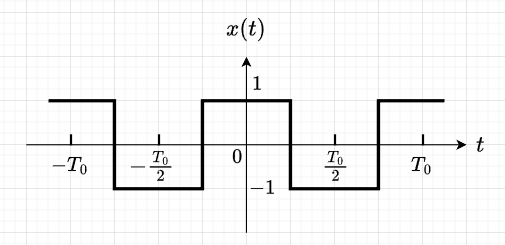
図2に示す方形波のフーリエ級数を求める。\(x(t)\)は偶関数なので、\(b_n=0\)、また、平均値は0なので、\(a_0=0\)である。$$a_n = \frac{4}{T_0} \int_{0}^{T_0/2} x(t) \cos n\omega_0 t dt \\ =\frac{4}{T_0} \left\{\int_{0}^{T_0/4} \cos n\omega_0 t dt - \int_{T_0/4}^{T_0/2} \cos n \omega_0 t dt \right\} \\ = \frac{4}{T_0} \left\{ \frac{1}{n \omega_0} \left[ \sin n\omega_0 t \right]_0^{T_0/4} - \frac{1}{n \omega_0} \left[ \sin n \omega_0 t\right]_{T_0/4}^{T_0/2} \right\} \\ = \frac{4}{T_0} \frac{1}{n \omega_0} \left(2 \sin \frac{n \pi}{2} \right) \\= \frac{4}{n \pi} \sin \frac{n \pi}{2} = \frac{4}{\pi} \frac{(-1)^{n-1}}{2n-1}$$

Scilabスクリプト
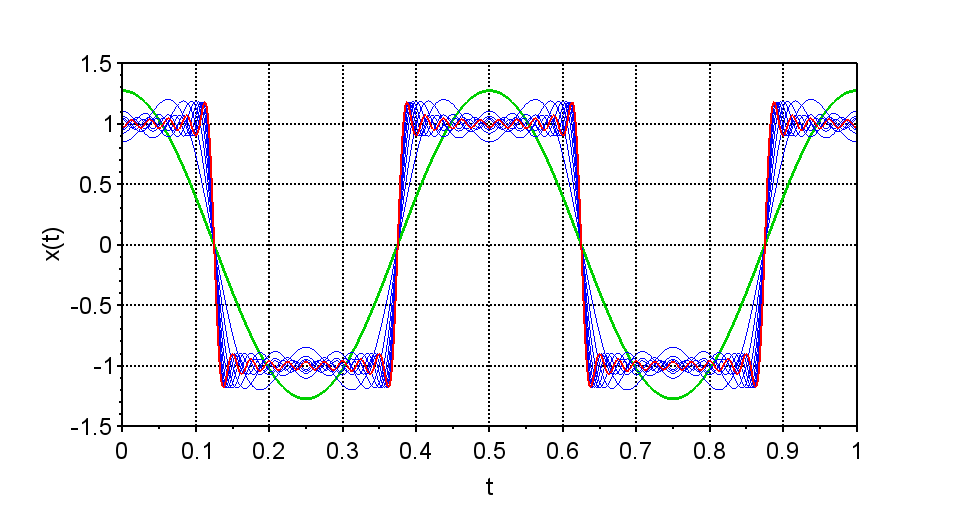
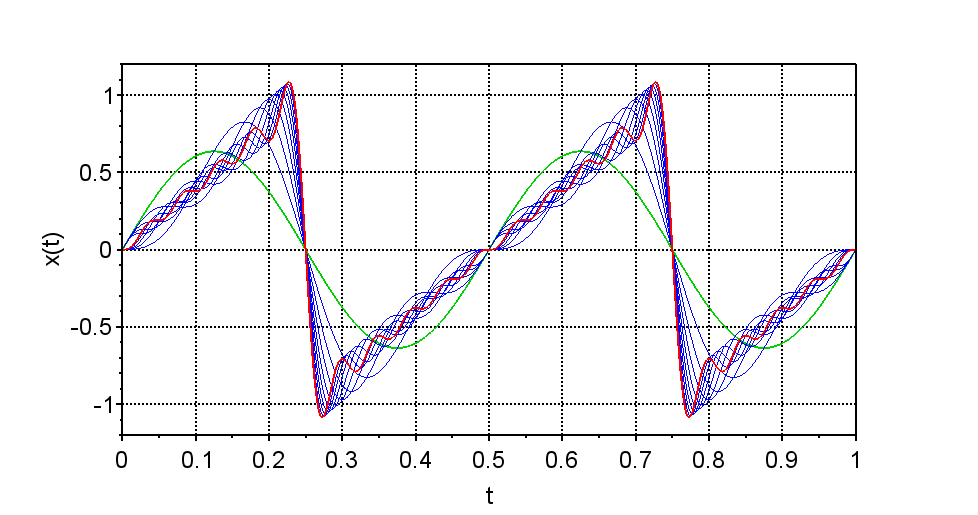
よって、$$x(t) = \frac{4}{\pi} \sum_{n=1}^{\infty} \frac{(-1)^{n-1}}{2n-1} \cos(2n-1)\omega_0 t \\ = \frac{4}{\pi}\left( \cos \omega_0 t - \frac{1}{3} \cos 3 \omega_0 t + \frac{1}{5} \cos 5 \omega_0 t - \cdots \right)$$となる。図3は上式で示した方形波のフーリエ級数を数値計算するためのScilabスクリプトである。実行結果を図4に示す。緑線は基本周波数成分(\(n=1\))を示している。赤線は\(n=10\)まで加算したときの\(x(t)\)である。このように\(n\)が増えるに従って方形波に近くなることが分かる。
のこぎり波のフーリエ級数
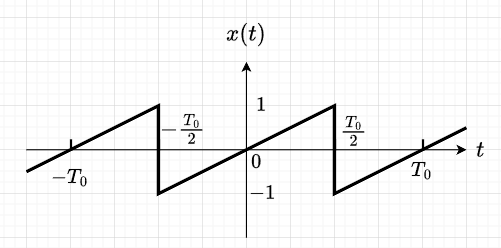
図5に示すのこぎり波のフーリエ級数を求める。\(x(t)\)は奇関数なので、\(a_n=0\)、また、平均値は0なので、\(a_0=0\)である。$$b_n = \frac{4}{T_0} \int_0^{T_0/2} x(t) \sin n \omega_0 t dt \\ = \frac{4}{T_0} \int_0^{T_0/2} \frac{2}{T_0} t \sin n \omega_0 t dt \\ = \frac{8}{T_0^2} \left\{\frac{-1}{n \omega_0} \left[t\cos n \omega_0 t \right]_0^{T_0/2} \\+ \frac{1}{n \omega_0} \int_0^{T_0/2} \cos n \omega_0 t dt \right\} \\ = \frac{8}{T_0^2} \left\{ \frac{-1}{n \omega_0} \frac{T_0}{2} \cos n \pi + \frac{1}{(n \omega_0)^2} \left[ \sin n \omega_0 t \right]_0^{T_0/2} \right\} \\ = \frac{2}{n \pi} (- \cos n \pi) = \frac{2}{n \pi} (-1)^{n+1}$$

Scilabスクリプト
よって、$$x(t) = \frac{2}{\pi} \sum_{n=1}^\infty \frac{(-1)^{n+1}}{n} \sin n \omega_0 t \\=\frac{2}{\pi}\left( \sin \omega_0 t - \frac{1}{2} \sin 2 \omega_0 t + \frac{1}{3} \sin 3 \omega_0 t - \cdots \right)$$となる。
図6は上式で示したのこぎり波のフーリエ級数を数値計算するためのScilabスクリプトである。実行結果を図7に示す。緑線は基本周波数成分(\(n=1\))を示している。赤線は\(n=10\)まで加算したときの\(x(t)\)である。このように\(n\)が増えるに従ってのこぎり波に近くなることが分かる。
複素フーリエ級数
式(1)の三角関数のフーリエ級数において、オイラーの公式より、$$ \cos n\omega_0 t = \frac{e^{j n\omega_0 t} + e^{-j n\omega_0 t} }{2} \\ \sin n \omega_0 t = \frac{e^{j n \omega_0 t} - e^{-j n \omega_0 t} }{2j}$$を使って、$$x(t) = \frac{a_0}{2} + \sum_{n=1}^{\infty} \left\{ \left(\frac{a_n - j b_n}{2} \right)e^{j n \omega_0 t} + \left(\frac{a_n + j b_n}{2}\right)e^{-j n \omega_0 t} \right\}$$となる。 ここで、$$c_0 = \frac{1}{2}a_0 , \;\;\; c_n = \frac{a_n - j b_n}{2} , \;\;\; c_n^* = \frac{a_n + j b_n}{2}$$(\(c_n\)と\(c_n^*\)は複素共役)とおくと、$$x(t) = \sum_{n = - \infty}^{\infty} c_n e^{j n \omega_0 t}$$が得られる。この式を複素フーリエ級数という。ここで、\(c_n\)を複素フーリエ係数といい、$$c_n = \frac{1}{T_0} \int_{-T_0/2}^{T_0/2} x(t) e^{- j n \omega_0 t}dt$$で求まる。また、$$|c_n| = \frac{1}{2} \sqrt{ a_n^2 + b_n^2} \\ \angle c_n = \phi_n = \tan^{-1}\left(\frac{b_n}{a_n}\right)$$である。ただし、\(c_0 = a_0/2\)である。 \(|c_n|\)を振幅スペクトル、\(\angle c_n\)を位相スペクトルという。なお、\(n\)は整数なので、振幅スペクトル、位相スペクトルは、\(n \omega_0\)だけで現れる不連続なスペクトル(線スペクトル)となる。
オイラーの公式
オイラーの公式は、$$e^{i\pi} =-1$$と\(e\)(ネイピア数)と\(\pi\)(円周率)と\(i\)(虚数単位)が一つの式にまとめられた美しい公式である。
工学では、虚数単位を\(j\)として、$$e^{j\omega t} = \cos \omega t + j \sin \omega t$$の形で使うことが多い。この式より、$$e^{-j \omega t} = \cos \omega t - j \sin \omega t$$なので、$$e^{j\omega t} + e^{-j \omega t} = 2 \cos \omega t \;\; \rightarrow \;\; \cos \omega t = \frac{e^{j\omega t} + e^{-j \omega t} }{2}$$また、$$e^{j\omega t} - e^{-j \omega t} = 2j \sin \omega t \;\; \rightarrow \;\; \sin \omega t = \frac{e^{j\omega t} - e^{-j \omega t} }{2j}$$と、三角関数が指数関数で表せる。
※オイラーの公式の証明については、https://rikeilabo.com/eulers-formula などを参照して欲しい。


“2. フーリエ級数” に対して1件のコメントがあります。
コメントは受け付けていません。