6. 論理関数の簡単化
論理関数の簡単化には、視覚的に判断できるカルノー図があるが、論理変数の種類が増えると図の表現が困難になり、実用的でない側面をもつ。この問題を解消する手法として、クワイン・マクラスキー法がある。
クワイン・マクラスキー法とは、論理関数を簡単化するための方法である。カルノー図と同様の目的で使われるが、コンピュータによる自動化に適しており、またブール関数が最簡形かどうか決定的に求めることができる。
クワイン・マクラスキー法は3段階からなる。
1)関数の主項をすべて求める
2)求めた主項を表にまとめ、必須項を求める
3)最簡易形を求める
クワイン・マクラスキー法
クワイン・マクラスキー法の基本原理は、次のブール代数の定理である。$$A \cdot B + A \cdot \overline{B} \rightarrow A \cdot (B + \overline{B}) =A \;\;\;\; \;\;(B + \overline{B} =1)$$ この定理を繰り返し使い、簡単化を進める。
例えば、$$Z = f(A,B,C,D) = \overline{A} \cdot \overline{B} \cdot C \cdot D + B \cdot C \cdot D + A \cdot B \cdot \overline{C} + A \cdot \overline{B} \cdot C \cdot D$$から、全ての最小項を求めると、$$f(A,B,C,D) = \overline{A} \cdot \overline{B} \cdot C \cdot D + (A + \overline{A}) \cdot B \cdot C \cdot D + A \cdot B \cdot \overline{C} \cdot (D + \overline{D}) + A \cdot \overline{B} \cdot C \cdot D \\= \overline{A} \cdot \overline{B} \cdot C \cdot D + A \cdot B \cdot C \cdot D + \overline{A} \cdot B \cdot C \cdot D + A \cdot B \cdot \overline{C} \cdot D + A \cdot B \cdot \overline{C} \cdot \overline{D} + A \cdot \overline{B} \cdot C \cdot D$$となる。
この論理式\(f(A,B,C,D)\)から主項を求める。例えば、\(\overline{A} \cdot \overline{B} \cdot C \cdot D\)と\(\overline{A} \cdot B \cdot C \cdot D\)から、$$\overline{A} \cdot C \cdot D \cdot(B + \overline{B}) = \overline{A} \cdot C \cdot D$$となるので、\(\overline{A} \cdot C \cdot D\)が求まる。図1のように、この操作を繰り返していくと、主項として、\(C \cdot D , \;\; A \cdot B \cdot \overline{C} , \;\; A \cdot B \cdot D\)が求まる。この際、\(A =1 , \overline{A}=0\)のように数値に置き換えるとプログラミングし易くなる。
ここで求まった主項から、$$f(A,B,C,D) = C \cdot D + A \cdot B \cdot \overline{C} + A \cdot B \cdot D$$が求まるが、この論理式には冗長な項が残っている。
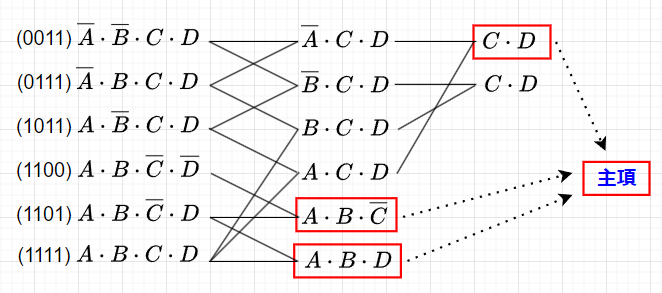
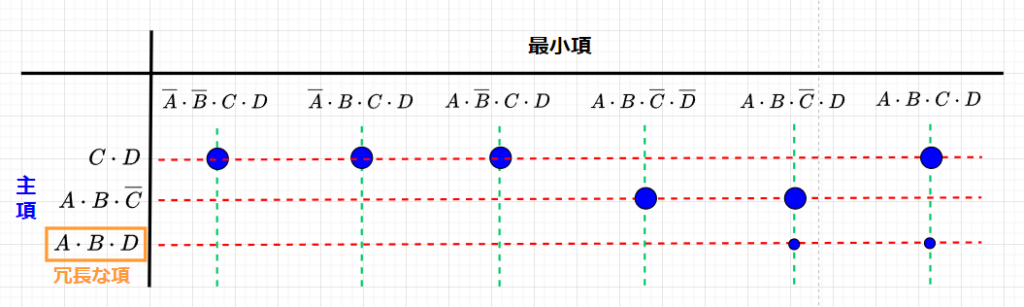
図2のように最小項と主項の図を作成すると、主項 \(C \cdot D\)と\(A \cdot B \cdot \overline{C}\)で、すべての最小項が実現できており、\(A \cdot B \cdot D\)が冗長な項であることが分かる。従って、最終的に簡単化された論理式は、$$Z=f(A,B,C,D) = C \cdot D + A \cdot B \cdot \overline{C}$$となる。
このようにクワイン・マクラスキー法は、手順はやや複雑であるが、論理変数が多くなっても、機械的に進めることができるため、プログラム化し易く、論理関数簡単化の自動化に適している。
クワイン・マクラスキー法による簡単化の例
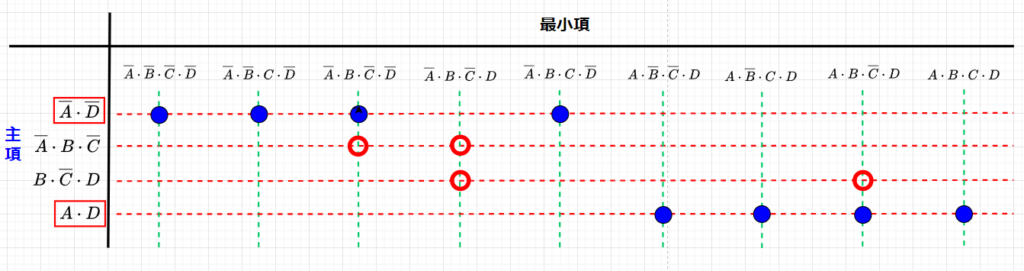
$$Z=f(A,B,C,D) =A \cdot \overline{B} \cdot D + A \cdot B \cdot D + \overline{A} \cdot \overline{C} \cdot \overline{D} + B \cdot \overline{C} \cdot D + \overline{A} \cdot C \cdot \overline{D}$$を簡単化する。
全ての最小項の形に整理すると、$$f(A,B,C,D) \\= A \cdot \overline{B} \cdot C \cdot D + A \cdot \overline{B} \cdot \overline{C} \cdot D \\+ A \cdot B \cdot C \cdot D + A \cdot B \cdot \overline{C} \cdot D \\+ \overline{A} \cdot B \cdot \overline{C} \cdot \overline{D} + \overline{A} \cdot \overline{B} \cdot \overline{C} \cdot \overline{D} \\+ A \cdot B \cdot \overline{C} \cdot D + \overline{A} \cdot B \cdot \overline{C} \cdot D \\+ \overline{A} \cdot B \cdot C \cdot \overline{D} + \overline{A} \cdot \overline{B} \cdot C \cdot \overline{D}$$と表せる。これより、主項を求めると、\(\overline{A} \cdot \overline{D}\)、\(\overline{A} \cdot B \cdot \overline{C}\)、\(B \cdot \overline{C} \cdot D\)、\(A \cdot D\)の4つとなる。ここで、図3により主項を選択すると、\(\overline{A} \cdot \overline{D}\)と\(A \cdot D\)は必須項であることが分かる。一方、\(\overline{A} \cdot B \cdot \overline{C}\)と\(B \cdot \overline{C} \cdot D\)の項(図の赤丸)は、どちらか一方の項が必須項となることが分かる。よって、簡単化した論理関数は、2通り考えられ、$$Z=f(A,B,C,D) = \overline{A} \cdot \overline{D} + A \cdot D + \overline{A} \cdot B \cdot \overline{C}$$または、$$Z=f(A,B,C,D) = \overline{A} \cdot \overline{D} + A \cdot D + B \cdot \overline{C} \cdot D$$となる。