19. 最適フィードバック制御
最適フィードバック制御は、制御系の性能を評価する関数(評価関数)を設定し、その関数値を最小化するようにフィードバックゲインを決定する制御方法である。評価関数は、制御系の応答の振る舞いを反映した関数で、応答の速度、精度、安定性などを考慮して設定する。
最適フィードバック制御は、古典制御でのフィードバック制御よりも優れた性能を実現することが可能であるが、制御系のモデルを正確に把握していないといけない、また、評価関数を適切に設定することが重要となる。
最適フィードバック制御全体の設計手順は次となる。
1.制御システムのモデルを構築する。
2.評価関数を定義する。
3.最適制御器を設計する。
4.最適制御器を評価する。
最適フィードバック制御は、制御システムの応答の特性を確実に満たすことができる強力な技術だが、最適制御器の設計は複雑であり、計算コストがかかる。
最適レギュレータの設計
制御対象を$$\boldsymbol{\dot{x}}(t) = \boldsymbol{Ax}(t) + \boldsymbol{Bu}(t) \;\;\; :\boldsymbol{A}(n \times n), \;\; \boldsymbol{B}(n \times m)$$とする。また、\((\boldsymbol{A,B})\)は可制御である。このシステムに対して、評価関数$$J = \int_0^{\infty} \left[ \boldsymbol{x}(t)^{T} \boldsymbol{Qx}(t) + \boldsymbol{u}(t)^{T}\boldsymbol{Ru}(t)\right]dt$$を最小にする制御入力\(\boldsymbol{u}(t)\)を求める。ここで、\(\boldsymbol{R}(m \times m), \; \boldsymbol{Q}(n \times n)\)は、設計仕様として与える重み行列である。\(\boldsymbol{R} \gt 0\):正定対称行列、\(\boldsymbol{Q} \ge 0\):半正定対称行列である。$$J = \int_0^{\infty} \boldsymbol{x}(t)^{T} \boldsymbol{Qx}(t) dt + \int_0^{\infty} \boldsymbol{u}(t)^{T}\boldsymbol{Ru}(t) dt$$と分けて考えると、前の項は、状態変数の2乗積分誤差で、後の項は、入力変数の2乗積分値、つまり、制御に必要なエネルギーを表している。従って、これらがともに小さくできたとき、よい制御システムといえる。しかし、これらの要求は相反するものなので、制御仕様から、重要な変数により大きい重みを課して\(J\)の最小化を目指すことになる。
評価関数\(J\)を最小にする制御は、状態フィードバック制御$$\boldsymbol{u}(t)=-\boldsymbol{Fx}(t)=-\boldsymbol{R}^{-1}\boldsymbol{B}^{T}\boldsymbol{Px}(t)$$で与えられる。ここで、\(\boldsymbol{P} \;\;\;(n \times n)\)は、リカッチ代数方程式$$\boldsymbol{A}^{T}\boldsymbol{P} + \boldsymbol{PA} + \boldsymbol{Q} - \boldsymbol{PBR}^{-1}\boldsymbol{B}^{T}\boldsymbol{P}=0$$を満たす正定対称行列である。最適レギュレータの設計手順は、次のようにまとめられる。
(1)可制御性をチェックする。
(2)評価関数の重み係数\(\boldsymbol{Q,R}\)を選定する。
(3)リカッチ代数方程式を解く。
(4)\(\boldsymbol{F}=\boldsymbol{R}^{-1}\boldsymbol{B}^{T}\boldsymbol{P}\)でフィードバック係数行列\(\boldsymbol{F}\)を求める。
最適制御法則
最適制御法則の詳細は以下のサイトを参照して欲しい。
http://ysserve.wakasato.jp/Lecture/ControlMecha2/node25.html
最適レギュレータの設計例
式(1)の制御対象に対して、式(2)の評価関数を最小にする制御則を求める。
$$\boldsymbol{\dot{x}}(t) = \begin{bmatrix} 0 & 1 \\ 0 & -1 \end{bmatrix}\boldsymbol{x}(t) + \begin{bmatrix} 0 \\ 1 \end{bmatrix} u(t) \cdots\cdots(1)$$ $$J = \int_0^{\infty}\left\{ \boldsymbol{x}^{T}(t)\boldsymbol{Qx}(t) + ru^2(t) \right\}dt \cdots\cdots(2)$$
(1)可制御行列$$U_c = [\boldsymbol{B} \;\;\;\;\ \boldsymbol{AB}]=\begin{bmatrix} 0 & 1 \\ 1 & -1\end{bmatrix}$$ でランク2より、可制御である。
(2)評価関数の重み係数を$$\boldsymbol{Q}=\begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix} , \;\;\;\; r=1$$に選定する。
(3)リカッチ代数方程式は、$$\boldsymbol{A}^{T}\boldsymbol{P} + \boldsymbol{PA} + \boldsymbol{Q} - \boldsymbol{PBR}^{-1}\boldsymbol{B}^{T}\boldsymbol{P} = \begin{bmatrix} 0 & 0 \\ 1 & -1 \end{bmatrix} \begin{bmatrix} p_{11} & p_{12} \\ p_{12} & p_{22} \end{bmatrix} + \begin{bmatrix} p_{11} & p_{12} \\ p_{12} & p_{22} \end{bmatrix} \begin{bmatrix} 0 & 1 \\ 0 & -1 \end{bmatrix} \\ + \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix} - \begin{bmatrix} p_{11} & p_{12} \\ p_{12} & p_{22} \end{bmatrix} \begin{bmatrix} 0 \\1 \end{bmatrix} 1 \begin{bmatrix} 0 & 1 \end{bmatrix} \begin{bmatrix} p_{11} & p_{12} \\ p_{12} & p_{22} \end{bmatrix} = 0$$よって、$$\begin{bmatrix} 0 & 0 \\ p_{11}-p_{12} & p_{12} - p_{22} \end{bmatrix} + \begin{bmatrix} 0 & p_{11} - p_{12} \\ 0 & p_{12} - p_{22} \end{bmatrix} + \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix} - \begin{bmatrix} p_{12}^2 & p_{12} p_{22} \\ p_{12} p_{22} & p_{22}^2 \end{bmatrix} = 0 $$従って、次の3本の連立方程式を解くことになる。$$p_{12}^2 = 1 \\ p_{11} - p_{12} - p_{12} p_{22} = 0 \\ 2(p_{12} - p_{22}) - p_{22}^2 +1 =0 $$解\(\boldsymbol{P}\)は3通り求まるが、その中で正定な行列は、$$\boldsymbol{P}=\begin{bmatrix} 2 & 1 \\ 1 & 1 \end{bmatrix}$$となる。
(4)以上よりフィードバック係数は、$$\boldsymbol{F}=r^{-1}\boldsymbol{B}^{T}\boldsymbol{P} = 1\begin{bmatrix} 0 & 1 \end{bmatrix} \begin{bmatrix} 2 & 1 \\ 1 & 1 \end{bmatrix} = \begin{bmatrix} 1 & 1 \end{bmatrix}$$と求まる。
Scilabを使った最適レギュレータの設計
Scilabを使うことで、容易にリカッチ代数方程式の解が求められ、フィードバック係数を決定できる。
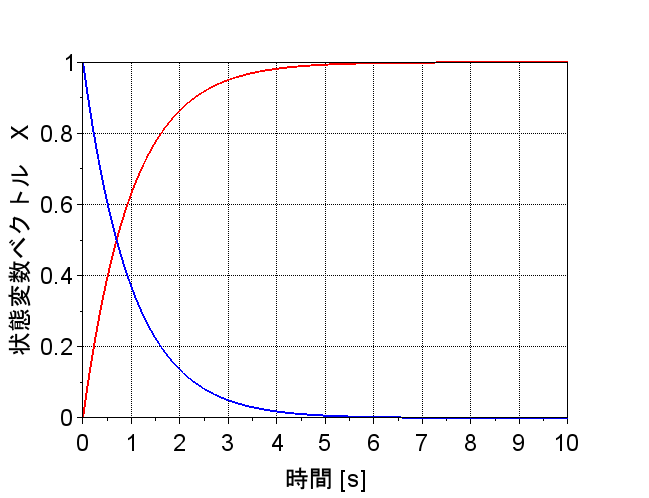
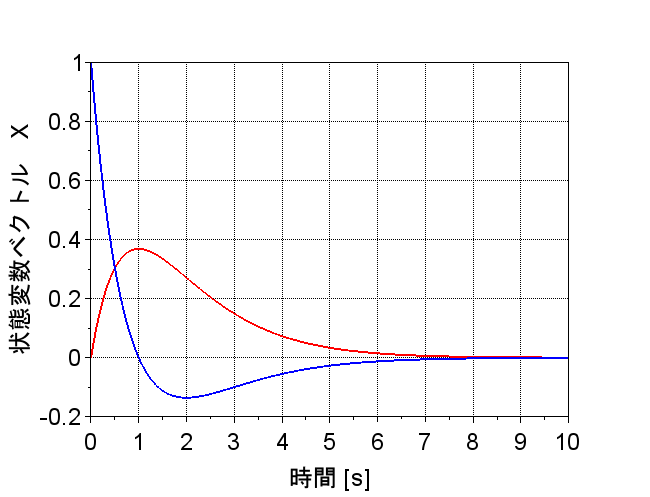
図「制御対象のインパルス応答特性」からこのシステムが不安定であることがわかる。一方、図「最適レギュレータのインパルス応答特性」では、状態変数ベクトルが全て0に収束しており、安定化できていることがわかる。
//最適レギュレータ
clear;clf();
i=%i;
//制御対象システムの定義
A=[0 1; 0 -1];
b=[0; 1];
c=[1 0 ; 0 1];
sysP=syslin('c',A,b,c);
//制御対象の固有値
evals=spec(A);
//可制御性のチェック
Uc=cont_mat(A,b);
n=rank(Uc);
//重み係数
Q=[1 0; 0 1]; r=1;
//状態フィードバック係数の決定
P=riccati(A,b*inv(r)*b',Q,'c','eigen');
f=inv(r)*b'*P
cpoles=spec(A-b*f); //極配置の確認
//制御対象のインパルス応答
t=0:0.01:10;
y0=csim('impulse',t,sysP);
scf(0);
plot(t',y0');
//最適レギュレータのインパルス応答
A2=A-b*f;
sysP2=syslin('c',A2,b,c);
y=csim('impulse',t,sysP2);
scf(1);
plot(t',y');