34. 結合回路
結合回路とは二つ以上の回路があって、一方の回路から他方の回路へ何らかの方法によって電力、電圧、電流が伝達される状態にあるとき、この二つの回路は電気的に結合されているといわれ、この回路は結合回路と呼ばれる。図「結合回路の種類」に様々な結合回路の例を示す。
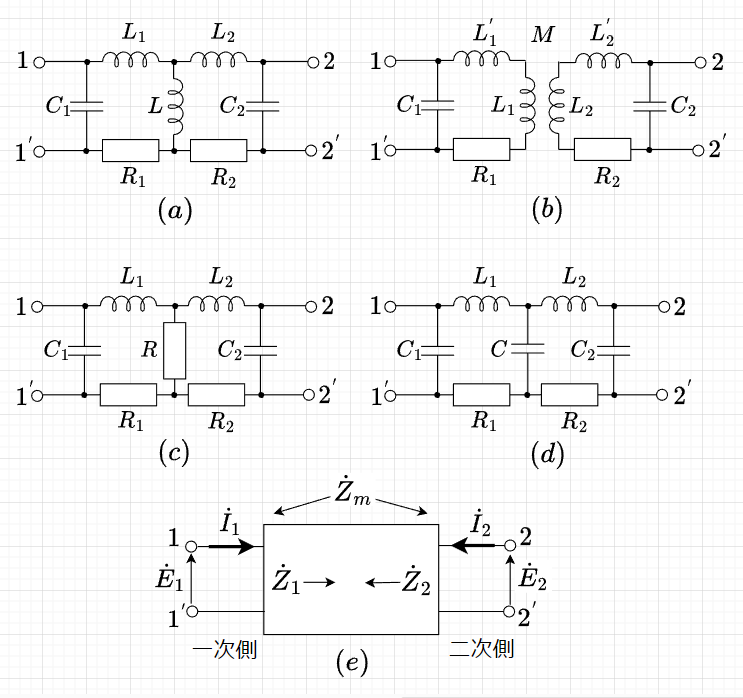
図\((a)\)は、自己誘導結合回路、図\((b)\)は、相互インダクタンス\(M\)による相互誘導結合回路、図\((c)\)は、抵抗結合回路、図\((d)\)は、容量結合回路である。図\((a)\)と\((b)\)のような結合は一括して電磁結合といい、図\((a)\)と\((c)\)、\((d)\)は導電結合しており、直接結合回路という。図\((b)\)は磁束を介しているので、間接結合回路ともいわれる。
結合係数
結合回路の結合の程度を表すために結合係数が用いられる。結合係数\(k\)は次のように定義される。$$k = \frac{\dot{Z}_m}{\sqrt{\dot{Z}_1 \dot{Z}_2}}$$ここで、図\((e)\)に示すように、\(\dot{Z}_1\)は二次側端子2-2'を開放したときの一次側端子1-1'から見たインピーダンス、\(\dot{Z}_2\)は一次側端子1-1'を開放した時二次側端子2-2'から見たインピーダンスである。\(\dot{Z}_m\)は、一次側と二次側の間の相互インピーダンスで、一般的に、端子1-1'以外が開放のとき、一次側の閉回路に流れる電流\(\dot{I}_1\)により二次側回路に生じる電圧\(\dot{E}_2\)と電流\(\dot{I}_1\)との比で、\(\dot{Z}_{21} = \dot{E}_2 / \dot{I}_1\)で与えられる。 この関係を入れ換えたとき、同様にして、\(\dot{Z}_{12} = \dot{E}_1 / \dot{I}_2\)で与えられる。回路が線形で左右同形なら、\(\dot{Z}_{12} = \dot{Z}_{21} = \dot{Z}_m\)になる。一般には、\(\dot{Z}_{12} ,\; \dot{Z}_{21},\; \dot{Z}_m\)は、表「\(\dot{Z}_{12} ,\; \dot{Z}_{21},\; \dot{Z}_m\)の回路別定義」のように定める。
| 電 磁 結 合 | 容 量 結 合 | 抵 抗 結 合 | |
| \(\dot{Z}_1\) | 一次回路の誘導リアクタンス | 一次回路の容量リアクタンス | 一次回路の抵抗 |
| \(\dot{Z}_2\) | 二次回路の誘導リアクタンス | 二次回路の容量リアクタンス | 二次回路の抵抗 |
| \(\dot{Z}_m\) | 一次、二次回路に共通の 誘導リアクタンス | 一次、二次回路に共通の 容量リアクタンス | 一次、二次回路に共通の抵抗 |
相互インダクタンス、相互リアクタンス
図「相互インダクタンスの回路」のような相互インダクタンス\(M\) [H]で結合された回路で、自己インダクタンス\(L_2\) [H] のコイルに角周波数\(\omega\) [rad/s] の正弦波交流電流\(i_2 = I_{m2} \sin \omega t \)[A] が流れたとすると、相互誘導作用によって、\(L_1\)の回路に$$e_1^{'} = M \left( - \frac{di_2}{dt} \right) \;\;\; [V]$$の電圧が生じる。 従って、相互インダクタンス\(M\)による電圧降下は、$$e_1 = M\frac{d i_2}{dt} \;\;[V]\;\; \cdots (1)$$と表せる。
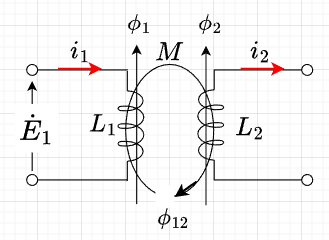
ここで、\(M\)は二つのコイルによって生じる磁束\(\phi_1 ,\; \phi_2\)が同方向のときには\(M \gt 0\)、互いに反対方向のときは\(M \lt 0 \)の値をとるものとする。式(1)は、複素インピーダンス表示を使うと$$\dot{E}_1 = M\frac{d\dot{I}_2}{dt} = j \omega M \dot{I}_2 \;\;[V]$$となり、\(\omega M \;[\Omega]\)を相互リアクタンスといい、\(X_M \; [\Omega]\)で表す。
また、相互誘導結合における結合係数は、$$\dot{Z}_m = j \omega M, \;\;\; \dot{Z}_1 = j \omega L_1, \;\;\; \dot{Z}_2 = j \omega L_2$$から、$$k = \frac{M}{\sqrt{L_1 L_2}}$$となる。ここで、\(L_1,\;L_2\)の両方に鎖交する磁束\(\phi_{12}\)のほかに、他方のコイルには鎖交しない磁束\(\phi_1,\;\phi_2\)が生じるため \(-1 \le k \le 1\) となり、漏れがなければ、\(k = \pm 1\)である。
結合回路の特性
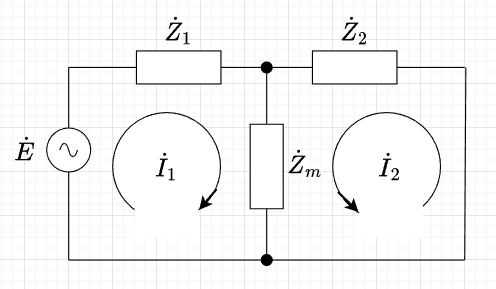
図「一般的な結合回路」において、一次側回路のインピーダンスを\(\dot{Z}_1\)、二次側回路のインピーダンスを\(\dot{Z}_2\)、共通のインピーダンス(相互インピーダンス)を\(\dot{Z}_m\)とすると、キルヒホッフの法則(KVL)から$$\dot{E} - \dot{Z}_1 \dot{I}_1 - \dot{Z}_m (\dot{I}_1 + \dot{I}_2) = 0 \\ \dot{Z}_m(\dot{I}_2 + \dot{I}_1) + \dot{Z}_2 \dot{I}_2 = 0$$となる。
よって、$$\dot{I}_1 = \frac{\dot{E}}{\dot{Z}_1 + \frac{\dot{Z}_m \dot{Z}_2}{\dot{Z}_2 + \dot{Z}_m}} , \;\;\;\;\; \dot{I}_2 = \frac{-\dot{E}}{\dot{Z}_1 + \dot{Z}_2 +\frac{\dot{Z}_1 \dot{Z}_2}{ \dot{Z}_m}}$$ 特に、$$\dot{Z}_1 = j\left\{\omega (L_1 - M) - \frac{1}{\omega C_1} \right\} , \;\;\; \dot{Z}_2 = j\left\{\omega (L_2 - M) - \frac{1}{\omega C_2} \right\} , \;\;\; \dot{Z}_m = j \omega M$$のとき、以下のことが言える。
1)一次回路に二次回路を結合させると、電源から見た抵抗が増加する。リアクタンスは、正負の値をとるため、増加する場合も減少する場合もある。
2)結合回路では共振周波数は2点で生じる。
3)共振曲線は双峰特性をもつ双峰共振曲線となる。結合を疎にする(\(k\)を小さくする)ほど両共振周波数は近づき、ある結合以下では、両者は一致する。結合係数\(k\)の大きい場合(おおよそ\(k \ge 0.5\))は密結合、小さい場合(おおよそ\(k \le0.2\))は疎結合と言われる。
結合回路の特性【例】(LTspice)
LTspiceを使って、双峰共振曲線を求めてみる。
各パラメータは、以下とする。
\(L_1 = 1\; mH , \; L_2 = 1 \; mH , \\ C_1 = 0.1 \; \mu F, \; C_2 = 0.1 \; \mu F \)として、結合係数\(k=0.05\;(M=0.05\; mH)\)と\(k=0.5\;( M=0.5\; mH)\)の場合を比較する。LTspiceで描いた回路図を「結合回路のシミュレーション」に示す。
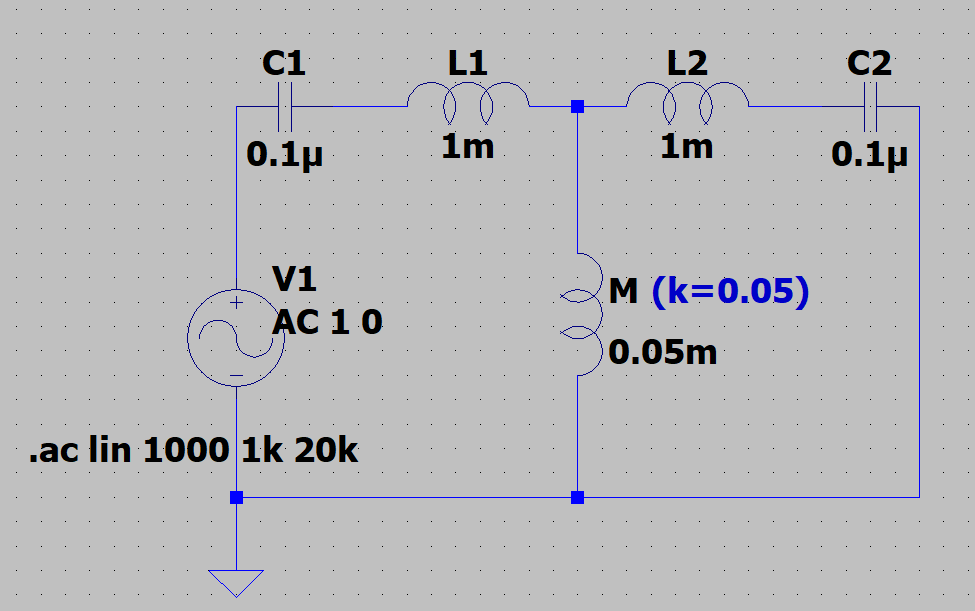

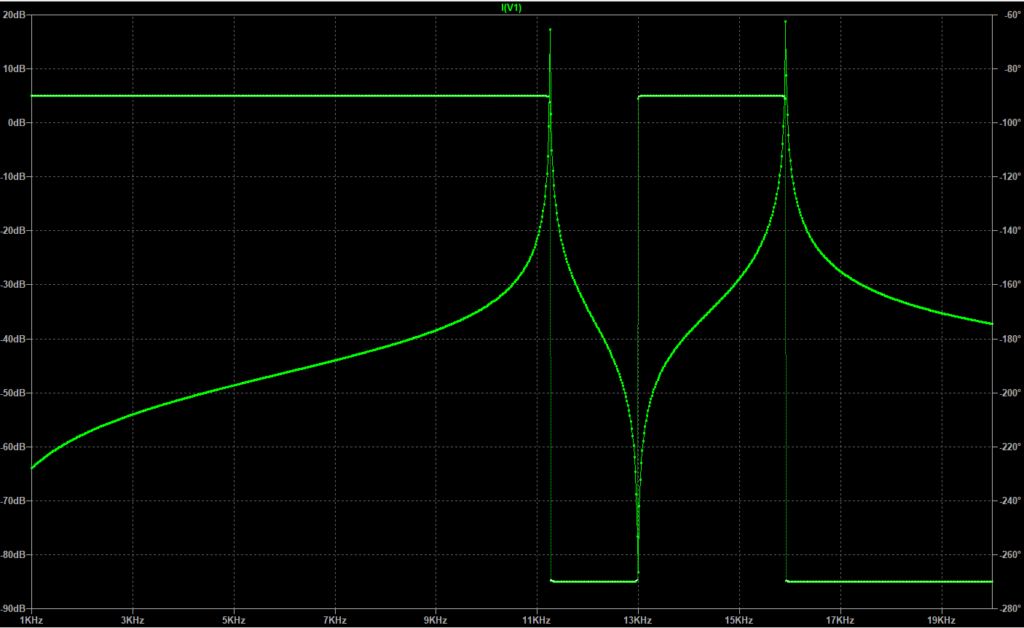
図のように電源電流\(I\)は双峰共振曲線を示すことが分かる。また、結合が疎なほど、つまり\(k\)が小さいほど両共振周波数が近づくことが分かる。


“34. 結合回路” に対して1件のコメントがあります。
コメントは受け付けていません。