7. 状態方程式と伝達関数

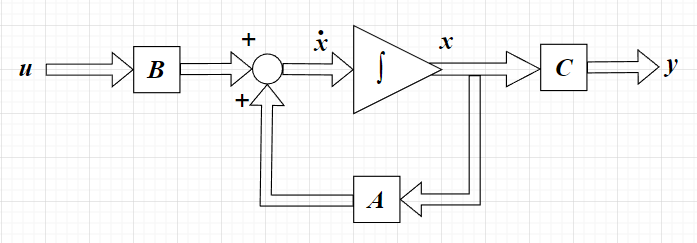
\(m\)入力、\(l\)出力の線形時不変システムを考える。
状態方程式、出力方程式は、$$\boldsymbol{\dot{x}}(t) = \boldsymbol{Ax}(t) + \boldsymbol{Bu}(t) \;\;\;\; \boldsymbol{A}(n \times n),\;\; \boldsymbol{B}(n \times m) \cdots \cdots (1)$$$$\boldsymbol{y}(t) = \boldsymbol{Cx}(t) \;\;\;\; \boldsymbol{C}(l \times n) \cdots \cdots (2)$$とする。\((1)\)式をラプラス変換すると、$$s\boldsymbol{X}(s) - \boldsymbol{x}(0) = \boldsymbol{AX}(s) + \boldsymbol{BU}(s) \\ (s\boldsymbol{I} -\boldsymbol{A})\boldsymbol{X}(s) = \boldsymbol{x}(0) + \boldsymbol{BU}(s) \\ \boldsymbol{X}(s) = (s\boldsymbol{I} -\boldsymbol{A})^{-1}\boldsymbol{x}(0) + (s\boldsymbol{I} -\boldsymbol{A})^{-1} \boldsymbol{BU}(s) $$ となる。\((2)\)式をラプラス変換すると、$$\boldsymbol{Y}(s) = \boldsymbol{CX}(s)$$なので、$$\boldsymbol{Y}(s) = \boldsymbol{C} (s\boldsymbol{I} -\boldsymbol{A})^{-1}\boldsymbol{x}(0) + \boldsymbol{C} (s\boldsymbol{I} -\boldsymbol{A})^{-1} \boldsymbol{BU}(s)$$となる。ここで、\(\boldsymbol{x}(0) = 0\)（初期値=0）と考えられるときは、$$\boldsymbol{Y}(s) = \boldsymbol{C} (s\boldsymbol{I} -\boldsymbol{A})^{-1} \boldsymbol{BU}(s)$$となり、$$\boldsymbol{G}(s) = \boldsymbol{C} (s\boldsymbol{I} -\boldsymbol{A})^{-1} \boldsymbol{B}$$の伝達関数行列が定義できる。\(\boldsymbol{G}(s)\)の各要素は、\(g_{ij}(s) = Y_i(s) / U_j(s)\)である。$$\boldsymbol{G}(s) = \boldsymbol{C} (s\boldsymbol{I} -\boldsymbol{A})^{-1} \boldsymbol{B} =\frac{\boldsymbol{C} \mathrm{adj}(s\boldsymbol{I} - \boldsymbol{A})\boldsymbol{B}}{|s\boldsymbol{I} - \boldsymbol{A}|} \cdots\cdots (3)$$ この分母=0は特性方程式である。特性方程式$$|s\boldsymbol{I} -A| = 0$$の根（特性根：\(\boldsymbol{A}\)の固有値）をシステムの極という。
１入力１出力（\(m = l = 1\)）のシステム（SISO）では、\((3)\)式の分子を零にする\(s\)、$$\boldsymbol{c}\;\mathrm{adj}(s\boldsymbol{I} - \boldsymbol{A})\boldsymbol{b} = 0$$の根を零点という（これが古典制御理論の零点である）。
多入力多出力システム（MIMO）における不変零点に関しては、
https://onsen-mula.org/wp-content/uploads/2017/04/SCI10_zeros_ppt.pdf　を参考にどうぞ。

状態方程式ー伝達関数【例】

【例１】１入力１出力のシステム（SISOシステム）における、状態方程式と伝達関数。

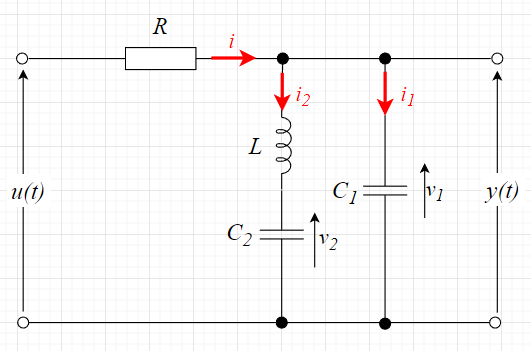
図「R-L-C 回路」について回路方程式を求める。\(R\)の電圧降下を\(v_R\)、\(R\)の電流を\(i\)、\(L\)の電圧降下を\(v_L\)、\(L\)の電流を\(i_2\)、\(C_1\)の電圧降下を\(v_1\)、\(C_1\)の電流を\(i_1\)、\(C_2\)の電圧降下を\(v_2\)とする。$$v_L = L\frac{di_2}{dt} ,\;\;\; i_2 = C_2\frac{dv_2}{dt} \\ i_1 = C_1\frac{dv_1}{dt} \\ v_R = i R = (i_1 + i_2)R = RC_1\frac{dv_1}{dt} + Ri_2 \\ v_1 = L\frac{di_2}{dt}+ v_2 \\ u(t) =v_R + v_L + v_2 = v_R + L\frac{di_2}{dt} + v_2$$

ここで、状態変数として、\(x_1 = v_1 ,\;\;\;x_2 = v_2,\;\;\; x_3 =i_2\)とおく。
$$v_L = L\dot{x}_3 ,\;\;\;\; i_2 = x_3 = C_2\dot{x}_2 \;\;\;\; i_1 = C_1 \dot{x}_1 \;\;\;\; x_1 = L\dot{x}_3 + x_2 \;\;\;\; x_1 = L\dot{x}_3 + x_2$$ \(i=i_1 + i_2 , v_r = iR\)より、$$u = \{C_1 \dot{x}_1 + C_2\dot{x}_2\}R + L\dot{x}_3 + x_2$$なので、\(\dot{x}_1, \; \dot{x}_2,\; \dot{x}_3\)について整理すると、$$\dot{x}_2=\frac{1}{C_2}x_3 , \;\;\;\; \dot{x}_3 = \frac{1}{L}x_1 - \frac{1}{L}x_2, \;\;\;\; \dot{x}_1 = -\frac{1}{RC_1}x_1 - \frac{1}{C_1}x_3 +\frac{1}{RC_1}u$$
これにより、状態方程式は、$$\begin{bmatrix} \dot{x_1} \\ \dot{x_2} \\ \dot{x_3} \end{bmatrix} = \begin{bmatrix} -\frac{1}{RC_1} & 0 & -\frac{1}{C_1} \\ 0 & 0 & \frac{1}{C_2} \\ \frac{1}{L} & -\frac{1}{L} & 0 \end{bmatrix} \begin{bmatrix} x_1 \\ x_2 \\ x_3 \end{bmatrix} + \begin{bmatrix} \frac{1}{RC_1} \\ 0 \\ 0 \end{bmatrix} u$$となる。また、出力方程式は、$$y = \begin{bmatrix} 1 & 0 & 0\end{bmatrix} \begin{bmatrix} x_1 \\ x_2 \\ x_3 \end{bmatrix} $$なので、$$\boldsymbol{A} = \begin{bmatrix} -\frac{1}{RC_1} & 0 & -\frac{1}{C_1} \\ 0 & 0 & \frac{1}{C_2} \\ \frac{1}{L} & -\frac{1}{L} & 0 \end{bmatrix} , \;\;\;\; \boldsymbol{b} = \begin{bmatrix} \frac{1}{RC_1} \\ 0 \\ 0 \end{bmatrix} , \;\;\;\ \boldsymbol{c} = \begin{bmatrix} 1 & 0 & 0\end{bmatrix} $$である。伝達関数は、$$\boldsymbol{c} (s \boldsymbol{I} - \boldsymbol{A})^{-1} \boldsymbol{b} = \frac{LC_2s^2+1}{C_1C_2LRs^3 + C_2Ls^2 + (C_1 + C_2)Rs+1}$$と求まる。
※この行列計算は比較的簡単ではあるが、Maximaを利用した。

【例２】多入力多出力システム（MIMOシステム）における伝達関数行列

状態方程式、出力方程式を$$\boldsymbol{\dot{x}} = \begin{bmatrix} 0 & 1 & 0 \\ 0 & 0 & 1 \\ 0 & 0 & 0 \end{bmatrix} \boldsymbol{x} + \begin{bmatrix} 0 & 1 \\ 0 & 0 \\ 1 & 0 \end{bmatrix} \boldsymbol{u} \\ \boldsymbol{y} =\begin{bmatrix} 3 & 1 & 0 \\ 2 & 3 & 1 \end{bmatrix} \boldsymbol{x}$$とする。このとき伝達関数行列は、$$\boldsymbol{G}(s) = \boldsymbol{C} (s\boldsymbol{I} -\boldsymbol{A})^{-1} \boldsymbol{B} \\ =\begin{bmatrix} 3 & 1 & 0 \\ 2 & 3 & 1 \end{bmatrix} \begin{bmatrix} s & -1 & 0 \\ 0 & s & -1 \\ 0 & 0 & s \end{bmatrix} ^{-1} \begin{bmatrix} 0 & 1 \\ 0 & 0 \\ 1 & 0 \end{bmatrix} \\=\begin{bmatrix} 3 & 1 & 0 \\ 2 & 3 & 1 \end{bmatrix} \begin{bmatrix} \frac{1}{s} & \frac{1}{s^2} & \frac{1}{s^3} \\ 0 & \frac{1}{s} & \frac{1}{s^2} \\ 0 & 0 & \frac{1}{s} \end{bmatrix} \begin{bmatrix} 0 & 1 \\ 0 & 0 \\ 1 & 0 \end{bmatrix} \\ = \begin{bmatrix} \frac{s+3}{s^3} & \frac{3}{s} \\ \frac{(s+1)(s+2)}{s^3} & \frac{2}{s} \end{bmatrix}$$と求まる。このようにMIMOシステムでは、伝達関数（入力出力の関係）は伝達関数行列として表される。