18. ノートンの定理

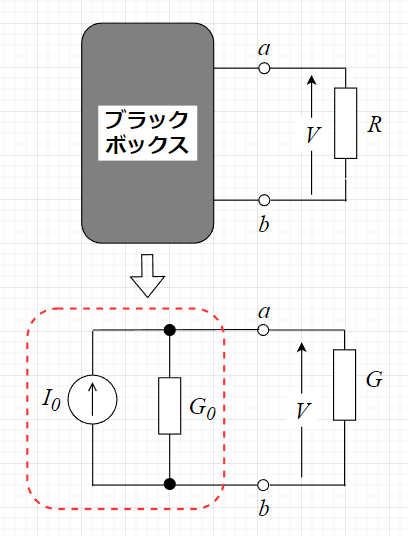
図「ノートンの定理」で”ブラックボックス”部分は、電源を含めた複雑な回路網である。この部分を単一の電流源と内部コンダクタンスに置き換えることを考える。
まず、

電圧\(V\)を求めたい部分、この図の場合、端子\(a,b\)のところでブラックボックス部分を短絡する。このときのa−b間に流れる電流は、ブラックボックス内の等価電流源から流れ出る電流\(I_0\)となる。つまり、電圧\(V=0\)としているので、短絡部分に流れる電流は\(I_0\)そのものとなる。
次に等価なコンダクタンス\(G_0\)を求める。端子\(a,b\)を開放し、ブラックボックス内部の電圧源は全て短絡、電流源は全て開放にする。これにより、端子a−bから見た内部コンダクタンス\(G_0\)が求まる。
以上により、下図の等価回路が求まる。この図より、求めたい電圧\(V\)は、$$V = \frac{I_0}{G + G_0}$$となる。
このようにノートンの定理を使えば、回路網の任意の場所の電圧を求めることができる。

ノートンの定理の使用【例】

図「ノートンの定理の使用例」で、左上図の青破線で囲んだ部分を\(I_0, G_0\)の等価回路に置き換えて、負荷抵抗（8Ω）の両端の電圧\(V\)を求める。
まず、端子\(a,b\)を短絡して、等価電流源を求める。図「等価電流源を求める」より、$$I_0 = \frac{20}{4} = 5 \; A$$となる。端子\(a,b\)を短絡したので、青破線内の\(8 \Omega\)は無関係になる。
次に端子\(a,b\)を開放し、青破線内の電圧源を短絡する。図「等価コンダクタンスを求める」より、等価コンダクタンス\(G_0\)は、$$G_0 = \frac{1}{4} + \frac{1}{8} = \frac{3}{8} \; S$$となる。

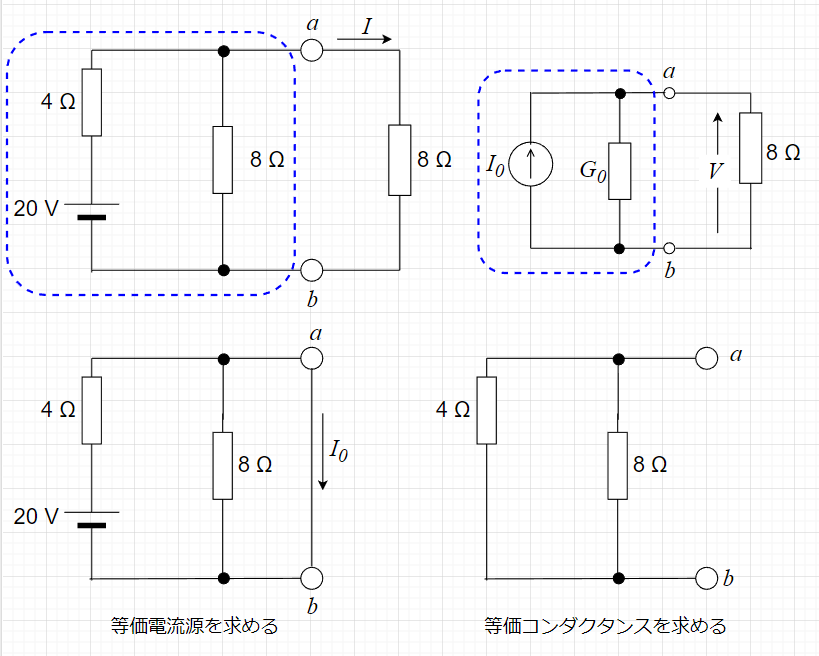
\(I_0 = 5 \; A\)、\(G_0 = \frac{3}{8} \; S\)となる。負荷のコンダクタンス\(G\)は、\(G = \frac{1}{8} \; S\)なので、負荷抵抗両端の電圧\(V\)は、$$V = \frac{I_0}{G_0 + G} = 10 \; V$$と求まる。
この例では、ブラックボックス内が簡単な回路網であるので、直並列回路の解析で済むが、多くの回路網はブラックボックス内が複雑なので、ノートンの定理の活用が有効となる。