6. 離散時間システムの周波数応答

パルス伝達関数の極、零点

離散時間システムのパルス伝達関数は、zの有理関数（ｚの多項式の比）で表される。$$G(z)=\frac{b_0z^m + b_1z^{m-1} + \cdots + b_m}{z^n + a_1z^{n-1} + \cdots + a_n}$$ 分子多項式=0、分母多項式=0として根を求め、分子多項式の根（零点）、分母多項式の根（極）とすると、パルス伝達関数は、$$G(z)=\frac{b_0(z - z_1)(z - z_2)\cdots (z - z_m)}{(z - p_1)(z - p_2)\cdots (z - p_n)}$$ \(G(z)\)の極\(p_i \;\; (i=1,2,\cdots,n) \)、\(G(z)\)の零点\(z_i \;\; (i=1,2,\cdots,m)\)と表せる。

パルス伝達関数の周波数応答（パルス周波数応答関数）

$$G(z)=\frac{b_0(z - z_1)(z - z_2)\cdots (z - z_m)}{(z - p_1)(z - p_2)\cdots (z - p_n)}$$ここで、ｚ変換の導出で説明したように\(z=e^{sT}\)である。周波数応答を考えるには、\(s \rightarrow j\omega\)とすれば良いので、\(z=e^{j\omega T}\)となり、さらにオイラーの公式を使うと$$z=e^{j\omega T}=\cos \omega T + j\sin \omega T$$と表せる。従って、\(G(z) \rightarrow G(e^{j\omega T})\)により、$$G(e^{j\omega T})=a(\omega) + jb(\omega)$$となる。ただし、\(a(\omega)\)、\(b(\omega)\)は\(\omega T\)の周期関数となる。
\(G(e^{j \omega T})=a(\omega)+jb(\omega)\)より、
利得：$$M=\left|G(e^{j \omega T})\right|=\sqrt{\{a(\omega)\}^2 + \{b(\omega)\}^2}$$位相：$$\phi=\arg\left\{G(e^{j \omega T})\right\}=\tan^{-1}\frac{b(\omega)}{a(\omega)}$$となる。

また、\(z=e^{j \omega T}=\cos \omega T + j\sin \omega T\)は周期関数なので、\(z=e^{j \omega T}=\cos( \omega T + 2\pi) + j\sin( \omega T + 2\pi)=e^{j (\omega T + 2\pi)}= e^{j(\omega + \frac{2\pi}{T})T} =e^{j(\omega +\omega_s)T} \)となる。
従って、\(z=e^{j \omega T}\)はサンプリング角周波数  \(\omega_s =\frac{2\pi}{T}\) の周期関数となっているので、\( G(e^{j\omega T} )\)  は、\(0 \le \omega \lt \frac{\pi}{T} (=\frac{\omega_s}{2})\)  の範囲を考えればよい。

【例】$$G(s)=\frac{\beta}{s + \alpha}$$ の離散化システムは、Z変換して、$$G(z)=\frac{b}{z -a}$$　\(a = e^{-\alpha T}\)　、\(b = \frac{\beta}{\alpha} \left( 1 - e^{- \alpha T}\right)\)となる。
\(z = e^{j \omega T}\)を代入すると、$$G(e^{j \omega T})=\frac{b}{e^{j \omega T} -a} = \frac{b}{\cos\omega T -a + j\sin \omega T}$$ よって、
利得：$$M=\left|G(e^{j \omega T})\right| = \frac{b}{\sqrt{a^2 -2a\cos \omega T + 1}}$$ 位相：$$\phi=\arg\left\{G(e^{j \omega T})\right\} = - \tan^{-1} \frac{\sin \omega T}{\cos \omega T -a} $$

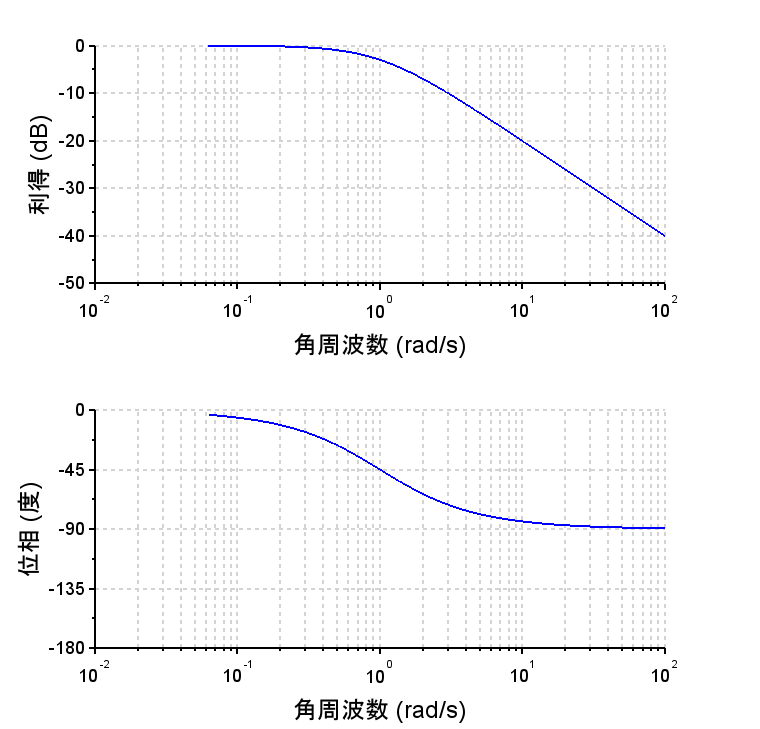
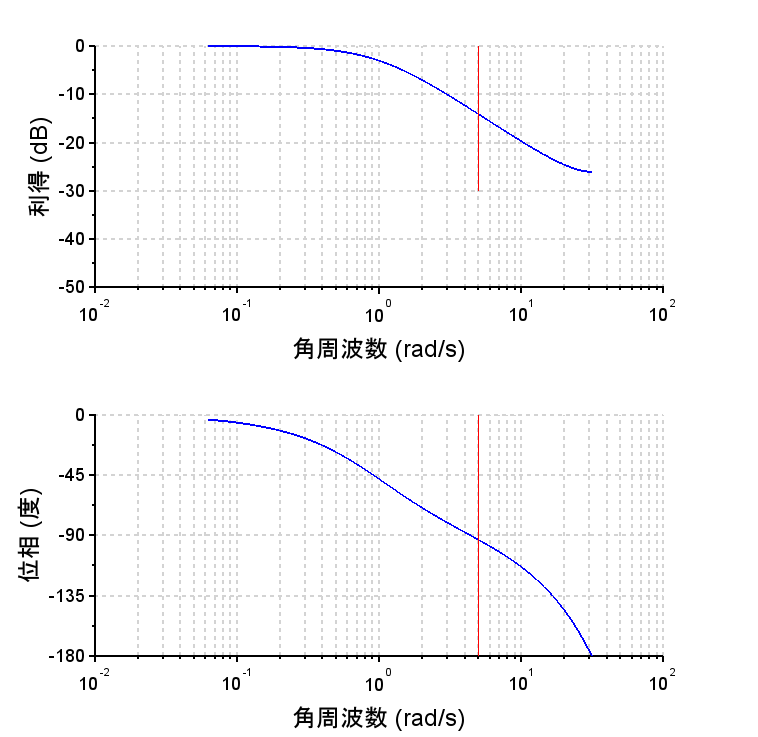
\(\alpha = 1\)、\(\beta =1\)、として、\(G(s)=\frac{1}{s+1}\)の1次遅れ系をサンプリング周期\(T = 0.1\)（サンプリング周波数\(f_s=10\)[Hz}、\(\omega_s=2\pi f_s\)[rad/s]）で離散化する。このとき、\(a=0.9048\)、\(b=0.0952\)となる。

Scilabのスクリプトで示すように、離散化の計算にはdscr()関数を使うとよい。

・連続時間系の\(G(s)\)の周波数応答では、\(G(s)\)は1次遅れ系で利得特性は、1[rad/s]において\(-3\)[dB]で、それ以上の周波数帯域では、\(-20\)[dB/dec]で利得が減衰する。また、位相遅れは\(-90\text{°}\)までである。
・離散時間系の\(G(z)\)の周波数応答は、周期関数なので\(\frac{\omega_s}{2}\)までの特性を見ればよい。
・離散時間系の利得特性は赤線が示す周波数範囲までは、ほぼ連続系と同様な特性であるが、それ以上の周波数帯域では歪んでいる。
・離散時間系の位相特性は赤線が示す周波数範囲内であってもかなり連続系とは異なっている。
・サンプリング周期\(T\)を短くすれば、歪の少ない範囲を広げることができるが、この歪は離散時間系の本質的な特徴であるので、常に意識する必要がある。

Scilabスクリプト

//パルス伝達関数の周波数応答
clear; clf;
s=%s; z=%z; e=%e;
T=0.1; a0=1,b0=1;
G=b0/(s+a0);
Gs=syslin('c',G);
//連続系ボード線図
scf(0);bode(Gs,0.01,100,'rad');
a=e^(-a0*T); b=b0*(1-e^(-a0*T))/a0;
//Gz=b/(z-a);
//Gzz=syslin(T,Gz);
Gzz=ss2tf(dscr(Gs,T)); /*連続系を離散系に変換*/
//離散系ボード線図
scf(1); bode(Gzz,0.01,100,'rad');