5. ラプラス変換の例

$$\delta(t)=\begin{cases} \infty \enspace (t=0) \\ 0 \enspace \enspace (t \neq 0)\end{cases}$$ $$\int_{-\infty}^{\infty} \delta(t) dt =1 $$　\(\delta(t)\)の定義より、$$\mathcal{L}\{\delta(t)\}=\int_0^{\infty}\delta(t) e^{-st}dt=1$$

単位インパルス関数（ディラックのデルタ関数）は、通常の関数とは異なる超関数であるが、非常に有用な関数であり、近似的な信号（インパルス信号）として取り扱う時、工学的に実用性の高いものである。
例えば、車体をハンマーで叩き（インパルスを与える）その打音を聞くことでヒビ等の機構の不具合点を見つけ出すことができる。

単位ステップ関数

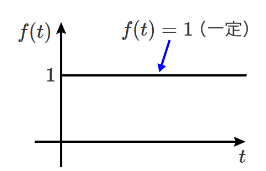
単位ステップ関数は、システムの時間応答を求める際に多く使われる。
$$f(t)=\begin{cases} 0 \enspace \enspace (t \lt 0) \\ 1 \enspace \enspace (t \geq 0)\end{cases}$$ より、\(\mathcal{L}\{f(t)\}=\int_0^{\infty}f(t)e^{-st}dt\\=\int_0^{\infty}e^{-st}dt \\=\left[-\frac{e^{-st}}{s}\right]_0^{\infty}\\=\frac{1}{s}\)

指数関数

$$f(t)=e^{-at} \enspace \enspace (a >0)$$ なので、\(\mathcal{L}\{f(t)\}=\int_0^{\infty}f(t)e^{-st}dt \\=\int_0^{\infty}e^{-at}e^{-st}dt\\=\int_0^{\infty}e^{-(s+a)t}dt\\=\left[-\frac{1}{s+a}e^{-(s+a)t}\right]_0^{\infty}\\=\frac{1}{s+a}\)

指数関数のラプラス変換は、制御工学の中でよく使用される。
特に伝達関数の特性を考えるとき、また、時間応答を求める際に、ラプラス逆変換を含めて良く表れる。