12. FIRディジタルフィルタ
ディジタルフィルタの構成
ディジタル信号処理の分野で、ディジタルフィルタは基本的で重要な技術で、様々な領域で活用されている。
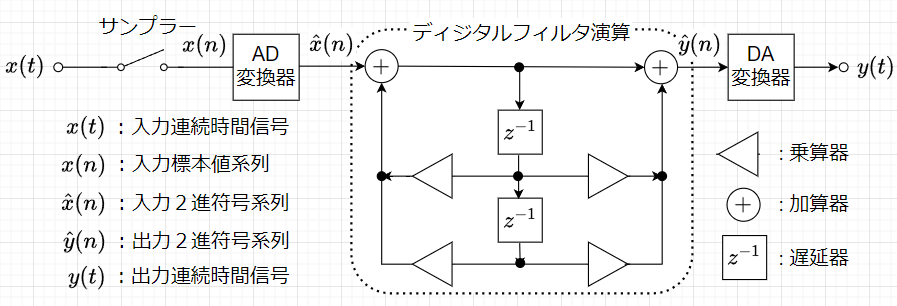
ディジタルフィルタは、特定周波数範囲の信号の伝送や除去などアナログフィルタと同じ目的で使用されるが、図1に示すように、連続時間の入力信号をサンプラーによる標本化、AD変換器による2進数のディジタル信号への変換、ディジタルフィルタ演算、DA変換器による連続時間の出力信号への変換、という操作を必要とする。これらの操作は煩雑ではあるが、以下のような様々な利点がある。
1)ディジタル演算によってフィルタ計算が行われるので、正確で、高精度に周波数選択できる。アナログフィルタで問題となる回路のばらつき、経年劣化、温度変化などの問題が無い。
2)メモリに設定したフィルタ係数をソフト制御で変更できるので、同一のハードウェア構成で、様々なフィルタ特性を容易に実現できる。
3)演算速度に余裕があれば、時分割多重処理により1フィルタあたりのコストを低減できる。
一方、欠点として以下がある。
1)高い周波数成分に対してリアルタイム処理するためには、高速なプロセッサやハードウェアが必要である。
2)入出力が連続時間信号のときは、AD、DA変換器を必要とする。
3)AD変換の際に生じる量子化雑音や、フィルタ演算でのまるめ誤差など避けられない問題がある。
また、ディジタルフィルタの周波数特性には周期性があることも、アナログフィルタと大きく異なる点である。
ディジタルフィルタの基本的な種類
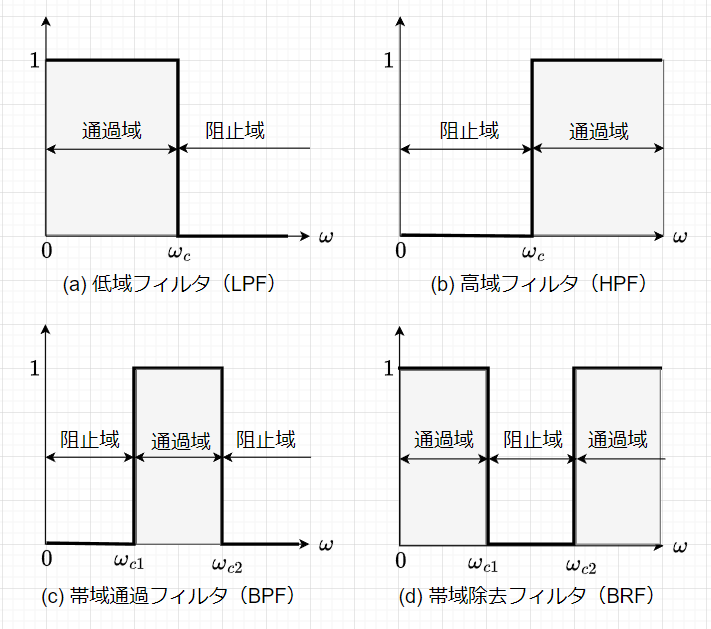
ディジタルフィルタの基本的な種類は、アナログフィルタと同様に、図2に示すように、低域フィルタ(LPF)、高域フィルタ(HPF)、帯域通過フィルタ(BPF)、帯域除去フィルタ(BRF)の4種類に分類できる。図2はそれぞれのフィルタの周波数特性を理想化して示しており、\(\omega_c\)をカットオフ周波数という。
FIRフィルタ
FIR(Finite Impulse Response) フィルタは、 有限インパルス応答フィルタ と呼ばれる。これは、ディジタルフィルタの一種で、入力信号に対して有限個の過去のデータのみを用いて出力信号を計算する。このため、有限の応答時間内に入力信号に対して有限の出力信号を生成する性質を持っている。FIRフィルタには以下の特徴がある。
・安定性:帰還ループを持たないため、常に安定した動作をする。
・高速処理:IIRフィルタに比べて処理速度が速い。
・設計の容易さ:IIRフィルタに比べて設計が容易である。
FIRフィルタは、ノイズ除去、スムージング、高周波カット、低周波カット、帯域通過など、さまざまな用途で使用される。
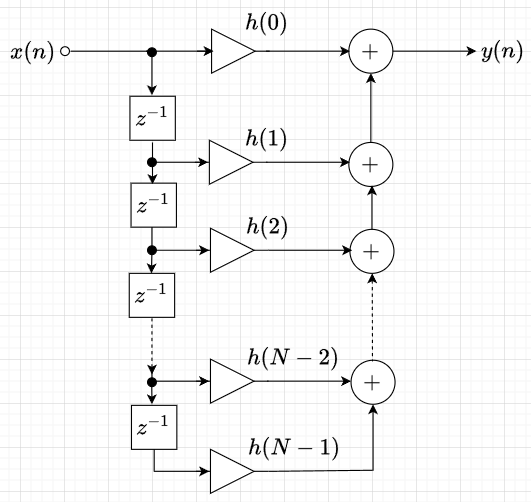
FIRフィルタは、インパルス応答が有限なシステムである。FIRフィルタの応答と伝達関数は、一般に以下のように表せる。$$y(n)= \sum_{k=0}^{N-1} h(k) x(n-k) \; \cdots\cdots(1)\\H(z) = \sum_{k=0}^{N-1} h(k) z^{-k} \; \cdots \cdots(2)$$
図3が式(1)を基にしたFIRフィルタの基本的な構成である。FIRフィルタの係数\(h(n)\)の値は、インパルス応答に等しい。FIRフィルタは帰還ループが無いので、安定性に問題がない。また、直線位相の設計が可能であるため、信号伝送用フィルタに適している。
直線位相FIRフィルタの周波数特性
直線位相特性は、フィルタの位相特性が周波数\(\omega\)の1次関数になっていることをいう。
【例】直線位相特性のシステム
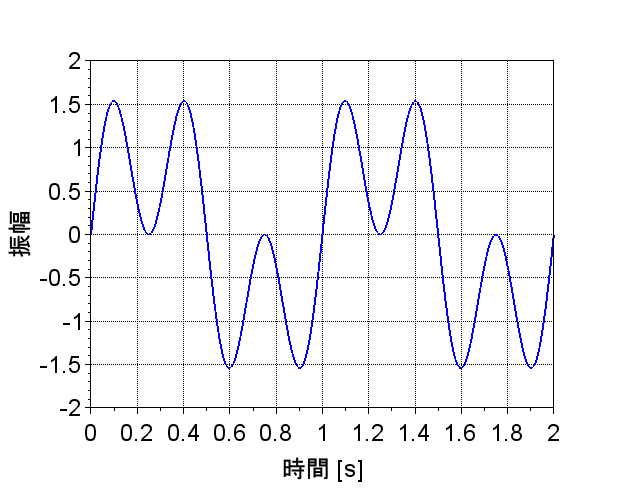
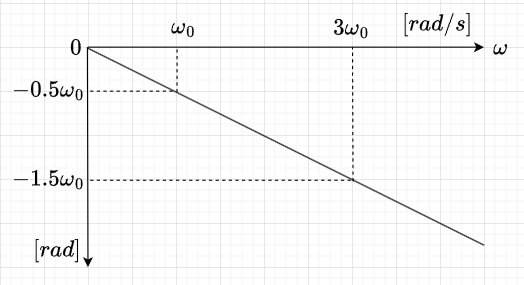
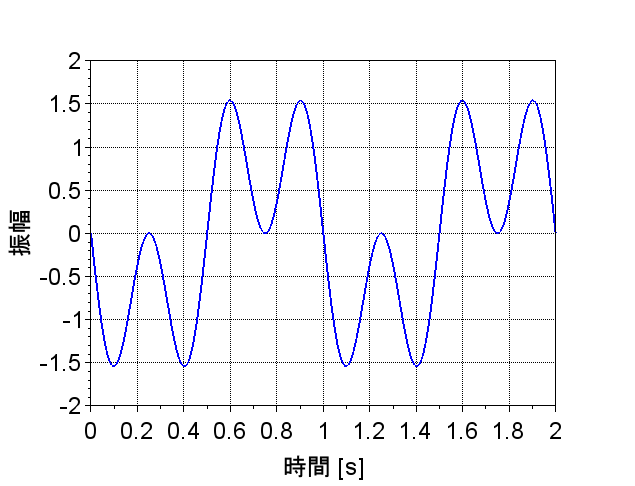
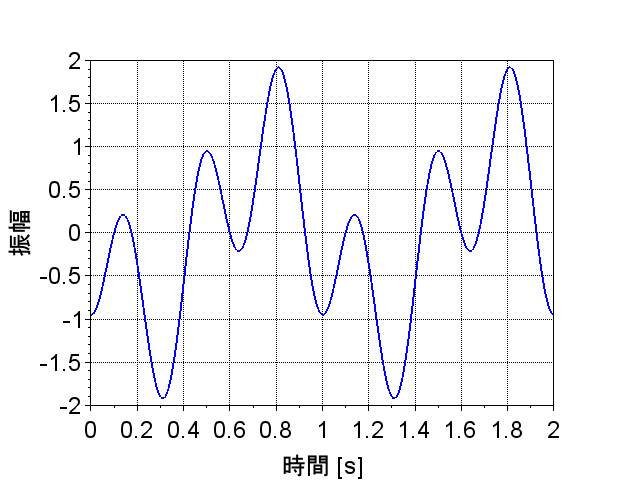
入力信号を$$x(t) = \sin(2\omega_0 t) + \sin(3\omega_0 t),\\ \;\;\omega_0 = 2 \pi f_0 , \;\; f_0=1$$とする。直線位相特性が\(\theta(\omega) = -0.5\omega\)のシステムに\(x(t)\)を印可した時の出力\(y(t)\)は、システムの利得を1として、$$y(t) = \sin\{2 \omega_0(t - 0.5)\} + \sin\{3 \omega_0(t - 0.5)\} \\= x(t -0.5)$$となる。図4に\(x(t)\)の波形を示す。図5に直線位相特性を示す。図6は、\(y(t)\)の波形である。システムの位相特性が\(\theta(\omega) = -0.5 \omega\)の直線位相特性なので、この場合、出力信号\(y(t)\)は入力信号\(x(t)\)に対して逆相の信号波形となるが、波形に変化は無く、波形全体の位相ずれ(時間軸で言うと平行移動)だけである。これに対して、\(3\omega_0\)成分の位相シフト量を直線位相特性から外れた\(1.2\omega_0\)とすると、出力信号\(y_1(t)\)は、$$y_1(t) =\sin\{2 \omega_0(t - 0.5)\} + \sin\{3 \omega_0(t - 0.4)\} $$となる。この場合の波形を図7に示す。このように非直線位相特性の場合、入力信号\(x(t)\)と異なった波形になってしまう。すなわち、位相歪みを生じることが分かる。
10. 離散時間システムの周波数特性で示したように、FIRフィルタの伝達関数\(H(z)\)(式(2))で\(z \rightarrow e^{j \Omega}\)と置き換えると、$$H(\Omega) = \sum_{n=0}^{N-1} h(n) e^{- j n \Omega}$$が得られる。この式から、FIRフィルタの周波数特性は、有限インパルス応答\(h(n)\)の離散フーリエ変換によって求められることが分かる。
直線位相特性の場合
非直線位相特性の場合
移動平均フィルタ(直線位相FIRフィルタの例)
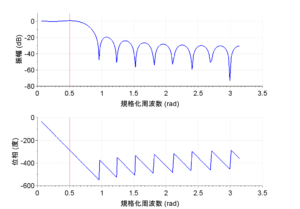
移動平均フィルタは、$$y(n) = \frac{1}{N} \sum_{k=0}^{N-1} x(n - k) \\ = \frac{1}{N} \left\{ x(n) + x(n-1) + \cdots + x(n-N+1)\right\}$$と表せる。ここで、\(N=3\)(3点の移動平均)とすると、$$y(n) = \frac{1}{3} \left\{ x(n) + x(n-1) + x(n-2) \right\}$$なので、インパルス応答は、$$h(n) = \frac{1}{3} \left\{ \delta(n) + \delta(n-1) + \delta(n-2) \right\}$$である。従って、離散フーリエ変換は、$$H(\Omega) = \frac{1}{3} \left(1 + e^{- j \Omega} + e^{-j 2 \Omega}\right) \\ = \frac{1}{3} \frac{1 - e^{- j 3 \Omega}}{ 1 - e^{- j \Omega}} \\= \frac{1}{3} \frac{e^{- j 3 \Omega /2}( e^{j 3 \Omega /2} - e^{-j 3 \Omega/2})}{e^{ -j \Omega /2}(e^{ j \Omega /2} - e^{- j \Omega /2})} \\ = \frac{1}{3} e^{- j \Omega} \frac{\sin(3 \Omega /2)}{\sin(\Omega /2)}$$となる。
※式の変形では級数の和とオイラーの公式を使った。
よって、$$|H(\Omega)| = \frac{1}{3} \left| \frac{\sin(3 \Omega /2)}{\sin(\Omega /2)} \right| \\ \angle{H(\Omega)} = \left\{ \begin{array}{l l} - \Omega & \left(\frac{\sin(3 \Omega /2)}{\sin(\Omega /2)} > 0 \right) \\ -\Omega \pm \pi & \left(\frac{\sin(3 \Omega /2)}{\sin(\Omega /2)} < 0 \right) \end{array} \right.$$となる。
周波数特性を図8に示す。この図より、移動平均フィルタが直線位相特性のFIRのLPFであることが分かる。
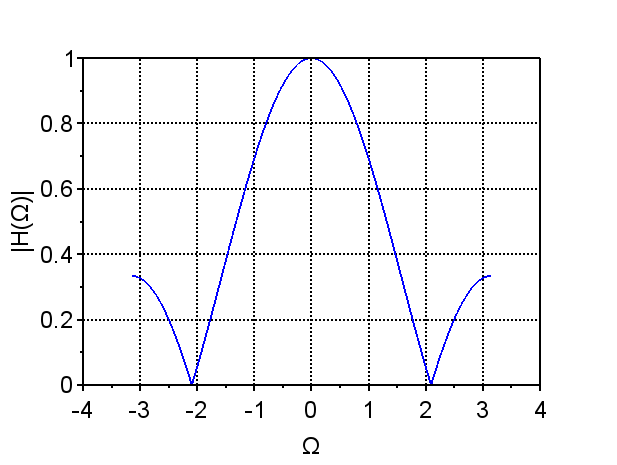
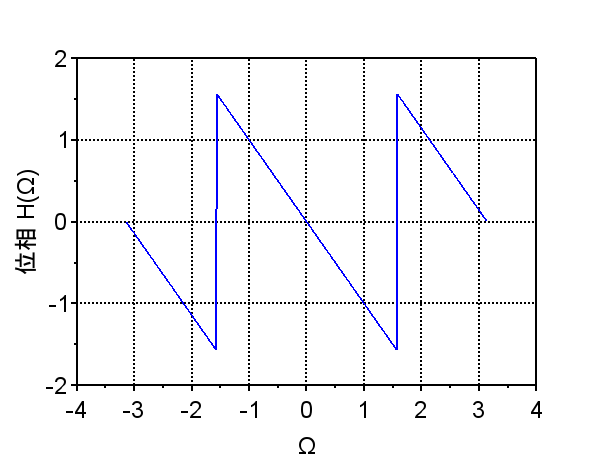
(\(N=3\))
Scilabスクリプト
//移動平均の周波数特性
clear; clf();
pi=%pi;
w=-pi:0.01:pi;
H=(1/3)abs(sin(3w/2)./sin(w/2));
th = atan(-(sin(w) + sin(2w)) ./ (1 + cos(w) + cos(2w)));
scf(0);plot(w,H);
scf(1);plot(w,th);