17. 状態遷移図、状態遷移表
状態遷移図(State Diagram)と状態遷移表(State Transition Table)は、有限状態機械(Finite State Machine)の設計や表現に用いられるツールで、シーケンシャルな制御や複雑な挙動を持つシステムのモデリングに使われる。(文章で書かれたソフトウェアの仕様を視覚的に捉えるために使われることも多い。)
状態遷移図は、有向グラフで構成され、システムの異なる状態と状態間の遷移を視覚的に表現する。状態遷移表は、状態遷移図の情報を表形式でまとめたものである。
状態遷移図
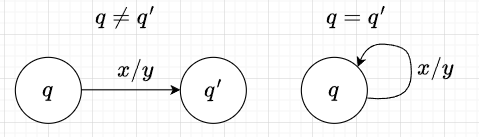
図1は、状態遷移図の基本記号である。で\(q\)や\(q'\)は状態、\(x\)は入力イベント、\(y\)は出力イベントを表している。
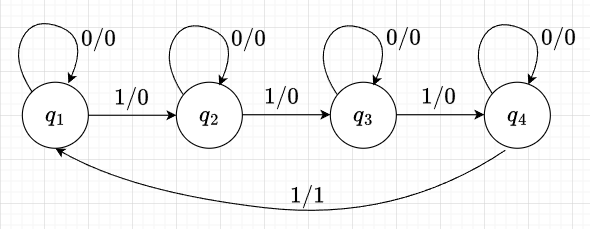
状態遷移図の簡単な例として、4進カウンタの状態遷移図を図2に示す。この図から、1が4回入力されて初めて1を出力して、それ以外は0のままであることが分かる。また、1が4回入力されると元の状態に戻る。
ストップウォッチの状態遷移図
ストップウォッチの状態遷移図を考える。仕様は以下とする。
・「スタート」「ストップ」「リセット」のボタンがある。
・「スタート」ボタンを押すと計時を開始する。
・「ストップ」ボタンを押すと計時を一時停止し、計測した時間を表示する。
・計測結果表示中に「スタート」を押すと計時を再開する。
・計測結果表示中に「リセット」を押すと計測時間をリセットする。
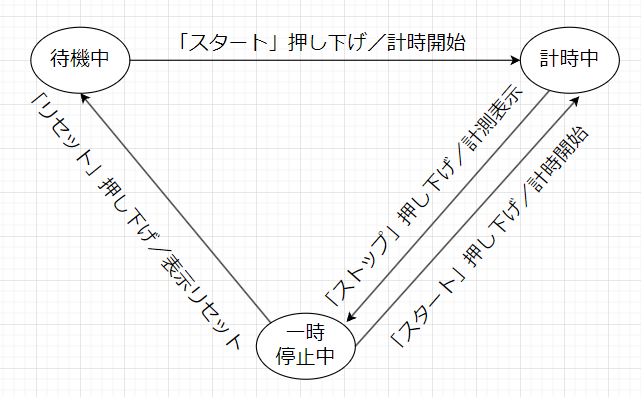
図3がストップウォッチの状態遷移図である。状態遷移図を作る利点は、仕様書を追いかけなくても一目で全体像が把握できる点にある。
自動販売機の状態遷移図
以下の自動販売機を考える。
・50円と100円硬貨が投入できる。
・150円以上投下されたらジュースとお釣りを出す。
図4が状態遷移図である。初期状態\(Q_0\)から、50円硬貨が投入された場合は、\(Q_{50}\)の状態に遷移する。\(Q_{50}\)の状態で50円投入された場合は、\(Q_{100}\)に遷移し、100円投入された場合は、ジュースを出して初期状態\(Q_0\)に遷移する。初期状態\(Q_0\)から、50円硬貨が投入された場合は、(Q_{100}\)の状態に遷移する。\(Q_{100}\)の状態で50円投入された場合は、ジュースを出して初期状態\(Q_0\)に遷移する。(Q_{100}\)の状態で100円投入された場合は、ジュースとお釣りを出して初期状態\(Q_0\)に遷移する。
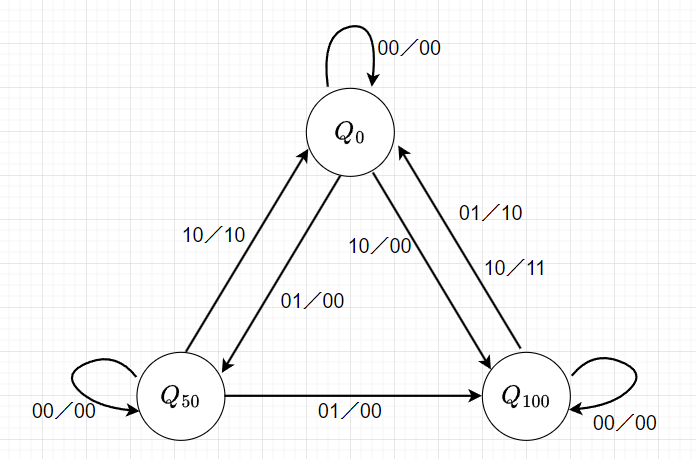
\(Q_0\):初期状態
\(Q_{50}\):内部に50円ある状態
\(Q_{100}\):内部に100円ある状態
入力/出力
入力01:50円投入
入力10:100円投入
出力10:ジュースを出す
出力01:お釣りを出す
出力11:ジュースとお釣りを出す
状態遷移表
RS-FFの状態遷移表
表1はRS-FFの状態遷移表である。この表において、\(Q_{n+1}\)で1になる場合に着目すると以下の式が成立する。$$Q_{n+1} =\overline{Q_n} S_n \overline{R_n} + Q_n \overline{S_n} \overline{R_n} + Q_n S_n \overline{R_n} \\ = S_n \overline{R_n} (\overline{Q_n} + Q_n) + Q_n \overline{S_n} \overline{R_n} \\ = S_n \overline{R_n} + Q_n \overline{S_n} \overline{R_n}$$また、禁止に着目すると、$$R_n S_n = 0$$この式が成立するには、\(R\)または\(S\)は0でなければならないことを意味する。
| \(Q_n\) | \(\overline{Q_n}\) | \(S_n\) | \(R_n\) | \(Q_{n+1}\) | \(\overline{Q_{n+1}}\) | |
| 0 | 1 | 0 | 0 | 0 | 1 | 保持 |
| 0 | 1 | 0 | 1 | 0 | 1 | リセット |
| 0 | 1 | 1 | 0 | 1 | 0 | セット |
| 0 | 1 | 1 | 1 | \(\phi\) | \(\phi\) | 禁止 |
| 1 | 0 | 0 | 0 | 1 | 0 | 保持 |
| 1 | 0 | 0 | 1 | 0 | 1 | リセット |
| 1 | 0 | 1 | 0 | 1 | 0 | セット |
| 1 | 0 | 1 | 1 | \(\phi\) | \(\phi\) | 禁止 |
\(R_n S_n = 0\)を使うと、$$Q_{n+1} = \overline{R_n} \overline{S_n} Q_n + \overline{R_n} S_n + R_n S_n \\ = \overline{R_n} \overline{S_n} Q_n + S_n (\overline{R_n} + R_n) \\ = \overline{R_n} \overline{S_n} Q_n + S_n \\ = \overline{R_n} Q_n \overline{S_n} + S_n(1 + \overline{R_n} Q_n) \\= \overline{R_n} Q_n (\overline{S_n} + S_n) + S_n \\= \overline{R_n} Q_n + S_n$$となる。この式をRS-FFの特性方程式という。この方程式は、次のように解釈できる。
1.\(S_n=1\) の場合、次の出力\(Q_{n+1}\)は1にセットされる。
2.\(S_n=0\)かつ\(R_n=0\)の場合、次の出力\(Q_{n+1}\)は前回の出力\(Q_n\)を保持する。
3.\(S_n=0\)かつ\(R_n=1\)の場合は、次の出力\(Q_{n+1}\)は0にリセットされる。
JK-FFの状態遷移表
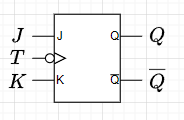
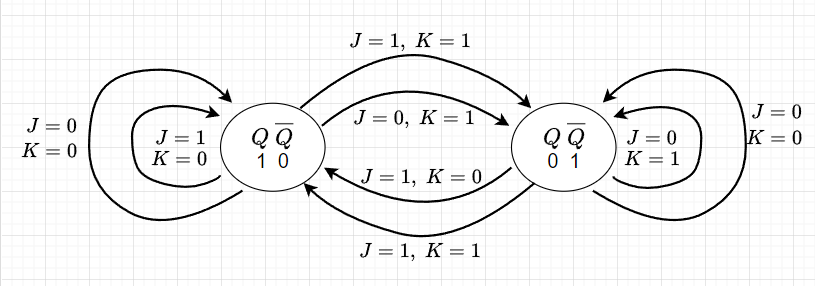
表2は図5に示すJK-FFの真理値表である。この表より、図6のJK-FFの状態遷移図が描ける。
また、状態遷移表は、表3のようになる。この表から\(Q_{n+1}\)は、以下の式で表せる。$$Q_{n+1} = \overline{J_n} \;\overline{K_n} T_n Q_n + J_n \overline{K_n}T_n \cdot 1 + J_n K_n T_n \overline{Q_n} \\+ \overline{J_n} \;\overline{K_n} \;\overline{T_n}Q_n + \overline{J_n} K_n \;\overline{T_n}Q_n \\+ J_n \overline{K_n} \;\overline{T_n}Q_n + J_n K_n \overline{T_n}Q_n$$この式を簡単化すると、$$Q_{n+1} = \overline{T_n}Q_n + \overline{K_n}Q_n + J_n T_n \overline{Q_n} \\= (\overline{T_n} + \overline{K_n})Q_n + J_n T_n \overline{Q_n}$$となる。この式はクロック\(T_n\)を含めたJK-FFの特性方程式である。ここで、\(T_n =1\)とすると、$$Q_{n+1} = \overline{K_n}Q_n + J_n \overline{Q_n}$$となり、表2の真理値表を満たすJK-FFの特性方程式となる。
| \(J\) | \(K\) | \(Q\) | \(\overline{Q}\) | |
| 0 | 0 | \(Q\) | \(\overline{Q}\) | 保持 |
| 0 | 1 | 0 | 1 | リセット |
| 1 | 0 | 1 | 0 | セット |
| 1 | 1 | \(\overline{Q}\) | \(Q\) | 反転 |
| \(J_n\) | \(K_n\) | \(T_n\) | \(Q_{n+1}\) | |
| 0 | 0 | 1 | \(Q_n\) | 保持 |
| 0 | 1 | 1 | 0 | リセット |
| 1 | 0 | 1 | 1 | セット |
| 1 | 1 | 1 | \(\overline{Q_n}\) | 反転 |
| 0 | 0 | 0 | \(Q_n\) | 保持 |
| 0 | 1 | 0 | \(Q_n\) | 保持 |
| 1 | 0 | 0 | \(Q_n\) | 保持 |
| 1 | 1 | 0 | \(Q_n\) | 保持 |
特性方程式を使ったカウンタの設計
JK-FFによる3進同期式カウンタ
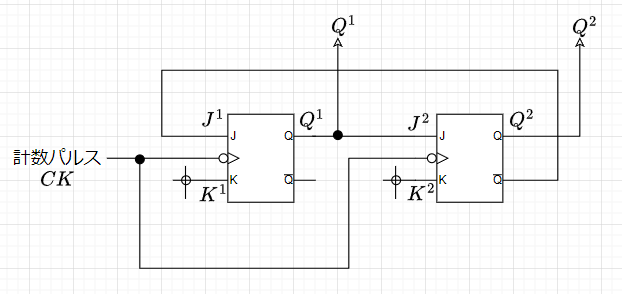
表4が3進カウンタの状態遷移表である。\(Q^2\)は2桁目、\(Q^1\)は1桁目を意味している。表4より、$$Q_{n+1}^2 = \overline{Q_n^2} Q_n^1 = (\overline{Q^2} Q^1)_n \cdots(1)\\ Q_{n+1}^1 = \overline{Q_n^2} \;\overline{Q_n^1} = (\overline{Q^2} \;\overline{Q^1})_n \cdots (2)$$と書ける。ここで、JK-FFの特性方程式\(Q_{n+1} = \overline{K_n}Q_n + J_n \overline{Q_n}\)を使うと、2桁目は、$$Q_{n+1}^2 = (\overline{K^2}Q^2 + J^2 \overline{Q^2})_n $$なので、これと(1)式を比較し、\(K^2=1\)、\(J^2 = Q^1\)が求まる。同様に、1桁目は、$$Q_{n+1}^1 = (\overline{K^1}Q^1 + J^1\overline{Q^1})_n$$なので、これと(2)式を比較し、\(K^1=1\)、\(J^1=\overline{Q^2}\)が求まる。以上から、回路は図7のように表せる。
| 計数パルス\(CK\) | \(Q_n^2\) | \(Q_n^1\) | \(Q_{n+1}^2\) | \(Q_{n+1}^1\) |
| 0 | 0 | 0 | 0 | 1 |
| 1 | 0 | 1 | 1 | 0 |
| 2 | 1 | 0 | 0 | 0 |