7. キルヒホッフの法則
キルヒホッフの法則は、電気回路の法則の一つで、回路中の電流と電圧の関係を表す法則である。キルヒホッフの法則は、回路内の任意の閉ループに沿って、電流と電圧の総和がゼロになるという法則である。具体的には、回路内のある点において、その点に流入する電流の総和は、その点から流出する電流の総和に等しくなる(KCL)。また、同様に回路内のある閉ループに沿って、電圧の総和もゼロになる(KVL)。
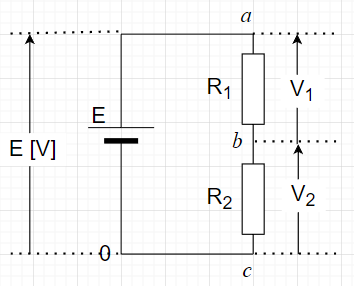
例えば、2つの抵抗が直列に接続された回路では、回路内の電圧が分割され、抵抗それぞれにかかる電圧の総和が回路内の電圧と一致する。また、回路内の電流は抵抗を通過するため、2つの抵抗にかかる電圧の総和は回路内の起電力に等しくなる。$$I = \frac{E}{R_1+R_2} \\ V_1 = R_1 I = \frac{R_1}{R_1 +R_2}E \\ V_2 = R_2 I = \frac{R_2}{R_1 +R_2}E$$よって、\(a\)点は\(E\;[V]\)、\(b\)点は、$$E - V_1=E\left( 1- \frac{R_1}{R_1 +R_2}\right) \\= E\frac{R_2}{R_1 +R_2}$$ \(c\)点は、$$E\frac{R_2}{R_1 + R_2} - V_2 = 0\;[V]$$となる。
キルヒホッフの第1法則(Kirchhoff's Current Law、KCL)
KCLは、ある点に流入する電流と、その点から流出する電流の総和が等しいことを表す。つまり、任意の交差点や接続点において、電流の保存則が成り立つことを示す。
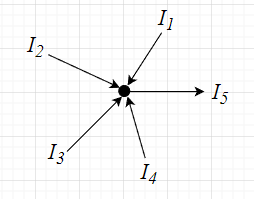
図「KCLの例」で考えると、流入電流は、\(I_1 , I_2 , I_3 , I_3\)で、流出電流は、\(I_5\)なので、$$I_1 + I_2 + I_3 + I_4 = I_5$$となる。
KCL
流入電流の総和=流出電流の総和
キルヒホッフの第2法則(Kirchhoff's Voltage Law、KVL)
KVLは、電気回路における基本的な法則の一つで、ある閉ループに沿って周回するとき、そのループに沿って電位をたどった時、電圧の総和がゼロになることを表す。
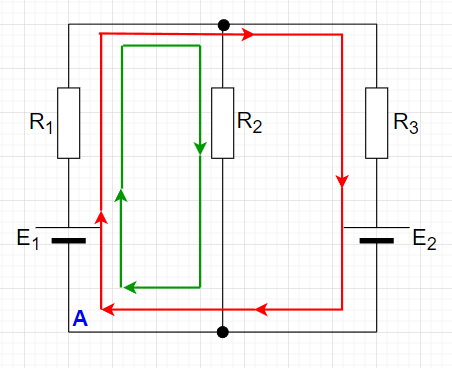
図「KVLの例」で考える。
・A点の電圧を基準電圧(0 V)とする。
・A点から閉回路(赤線や緑線)に従って電位をたどる。
・A点に戻るとそのときの電圧は基準電圧(0 V)となる。
KVL
閉回路に沿って電位をたどると電圧の総和は0 Vになる。
KCL、KVLによる回路解析
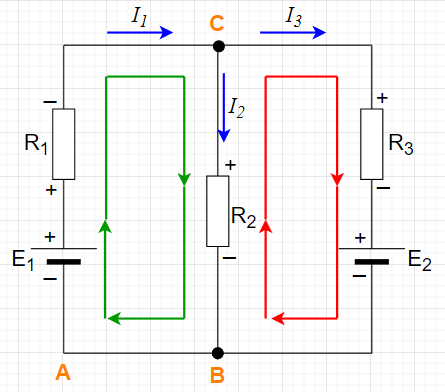
図「KCL、KVLによる回路解析」で、\(I_1,I_2,I_3\)を求めることを考える。
まず、電流の方向を仮定する。解析した結果、仮定した電流の方向が違っていたら、求まった電流値は負の値になる。
図「KCL、KVLによる回路解析」の場合、\(R_1\)には\(I_1\)の方向で電流が流れるとする。同様に、\(R_2\)には\(I_2\)の方向で、\(R_3\)には\(I_3\)の方向で電流が流れるとする。
\(I_1\)の方向に電流が流れるので、\(R_1\)における電圧は下側が高くて、上側が低いことになる。各抵抗の両端での電圧の高低が分かりやすいように、抵抗の電圧が高い方に「+」、電圧が低い方に「-」を記す。電源は電流が流れる方向に関係なく正極に「+」、負極に「-」を記す。(「+」「—」を記す作業は、解析に慣れれば必要ないが、KVLで電位をたどるときの間違いを防ぐのに有効な方法である。)
KCLより、C点において\(I_1\)は流入、\(I_2,I_3\)は流出なので、$$I_1 = I_2 + I_3$$である。
KVLより、A点から緑線の閉回路について、$$0 + E_1 -R_1I_1 -R_2I_2 = 0$$ となる。このとき、緑線に沿って、各素子に記した「-」から「+」のときには\(+\)(加算)で、「+」から「-」のときには\(-\)(減算)で式をたてる。
KVLより、B点から赤線の閉回路について、$$0 + R_2 I_2 - R_3 I_3 -E_2 =0$$となる。式を整理すると、$$I_1 -I_2 - I_3 = 0 \\ R_1 I_1 + R_2 I_2 = E_1 \\ R_2 I_2 - R_3 I_3 = E_2$$の連立方程式となる。求めたい未知数\(I_1, I_2, I_3\)にたいして、方程式が3つなのでこれを解けば、各電流\(I_1, I_2, I_3\)が求まることになる。連立方程式を行列で表すと$$\begin{bmatrix} 1 & -1 & -1 \\R_1 & R_2 & 0 \\ 0 & R_2 & -R_3 \end{bmatrix} \begin{bmatrix} I_1 \\ I_2 \\ I_3 \end{bmatrix} = \begin{bmatrix} 0 \\ E_1 \\ E_2 \end{bmatrix}$$ となり、$$\begin{bmatrix} I_1 \\ I_2 \\ I_3 \end{bmatrix} =\begin{bmatrix} 1 & -1 & -1 \\R_1 & R_2 & 0 \\ 0 & R_2 & -R_3 \end{bmatrix}^{-1} \begin{bmatrix} 0 \\ E_1 \\ E_2 \end{bmatrix}$$と\(I_1, I_2, I_3\)が求まる。これは、電卓やプログラムで簡単に解を得ることができることを示している。
また、求めた電流\(I_1, I_2, I_3\)より、抵抗\(R_1,R_2,R_3\)における電圧降下は、\(V_1=R_1I_1 \;\;, \;\;V_2=R_2I_2 \;\;, \;\;V_3=R_3I_3 \)と求まる。以上により、この回路の解析が完了する。
キルヒホッフの法則による回路解析の具体例
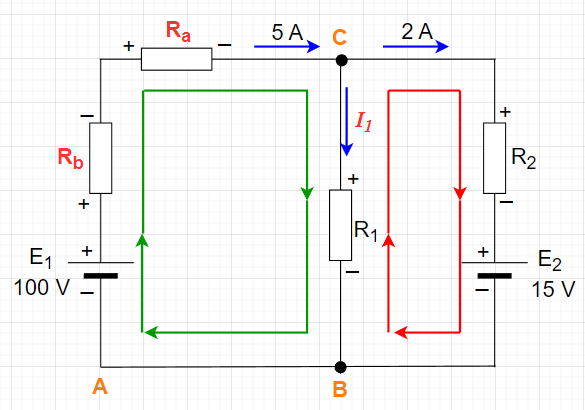
【例】図「回路解析例」において、\(E_1 = 100 V \;\;,\;\; E_2 = 15 V \\ R_a = 3\; \Omega \;\;,\;\; R_b = 2 \; \Omega\)とする。
このとき、\(I_1, R_1, R_2\)を求める。
KCLより、C点において、流入電流(5A)、流出電流(2A , \( I_1 \) )なので $$ 5\; A = 2 \; A + I_1 $$ よって、$$ I_1 = 3 \; A$$ KVLより、
緑線のループについて、A点を基準として、$$ E_1 - R_b \times 5 - R_a \times 5 - R_1 \times 3 = 0 \\ 100 - 2\times 5 - 3 \times 5 -R_1 \times 3 = 0 $$よって、$$R_1 = 25 \; \Omega $$ 赤線のループについて、B点を基準として、$$R_1 \times 3 - R_2 \times 2 - E_2 = 0 \\ R_1 \times 3 - R_2 \times 2 = 15 $$ よって、$$ R_2 = 30 \; \Omega$$ このように、KCL、KVLを使うことによって、回路網を解析できる。
※実際の回路では、非常に複雑な場合が多いので、式も多次元の連立方程式となる。このため、実践的にはコンピュータによるシミュレーションツールの活用やプログラムの作成が重要となる。


“7. キルヒホッフの法則” に対して5件のコメントがあります。
コメントは受け付けていません。