3. フーリエ変換

2024年2月11日 2024年2月12日

tctyam

フーリエ変換は、時間領域（または、空間領域）で表現された信号や関数を、周波数領域に変換する数学的手法である。時間領域とは、信号が時間の経過とともにどのように変化するかを表す領域であり、周波数領域とは、信号がどのような周波数の成分で構成されているかを表す領域である。フーリエ変換の基本的なアイデアは、信号を異なる周波数成分（正弦波や余弦波）の合成と見なすことであり、フーリエ級数の拡張となっている。フーリエ変換は、特定の信号がどのような周波数成分で構成されているかを分析し、周波数スペクトル（振幅スペクトル、位相スペクトル）を得るために使用される。フーリエ変換は、音声解析、画像解析、振動解析など、さまざまな分野で広く活用されている。

フーリエ変換の導出

フーリエ級数は周期信号を対象としているが、実際に扱う信号には非周期信号も多い。周期$T_0$の周期信号$x_{T_0}(t)$において、$T_0$を無限大に近づけると、$$x(t)=\lim_{T_0 \rightarrow \infty} x_{T_0}(t)$$は、非周期信号と見なせる。このように、フーリエ級数を$T_0 \rightarrow \infty$となるように拡張したものをフーリエ変換という。
複素フーリエ級数を式(1)に示す。$$x(t) = \sum_{n=-\infty}^{\infty} \left[\frac{1}{T_0} \int_{-T_0/2}^{T_0/2} x(\tau) e^{-j n \omega_0 \tau} d \tau \right] e^{j n \omega_0 t} \; \cdots (1)$$ここで、$\omega_0 = 2\pi / T_0$なので、式(1)は、式(2)のように書き直せる。$$x(t) = \frac{1}{2 \pi} \sum_{n=-\infty}^{\infty} \left[ \omega_0 \int_{-\pi/ \omega_0}^{\pi / \omega_0} x(\tau) e^{-j n \omega_0 \tau} d \tau \right] e^{j n \omega_0 t} \; \cdots (2)$$ $T_0 \rightarrow \infty$とすると、$\omega_0 = 2 \pi / T_0$は微小となり$d\omega$と表せ、$n \omega_0$は連続角周波数の$\omega$と表せる。また、全ての高調波にわたる総和$\sum_{n=-\infty}^{\infty}$の部分は$\omega$の全範囲にわたる積分となる。従って、式(2)は、$$x(t) = \frac{1}{2 \pi} \int_{-\infty}^{\infty} \left[ \int_{-\infty}^{\infty} x(\tau) e^{-j \omega \tau} d\tau \right] e^{j \omega t} d \omega \; \cdots (3)$$となる。ここで、$$X(\omega) = \int_{-\infty}^{\infty} x(t) e^{-j \omega t} dt = \mathcal{F} [x(t)] \; \cdots (4)$$を定義する。（$\mathcal{F}$は、フーリエ変換を意味する記号として使われることが多い。）
この$X(\omega)$を$x(t)$のフーリエ変換という。この式(4)を使うと、式(3)は、$$x(t) = \frac{1}{2 \pi} \int_{-\infty}^{\infty} X(\omega) e^{j \omega t} d \omega = \mathcal{F}^{-1} [X(\omega)] \; \cdots (5)$$と表せ、式(5)を逆フーリエ変換という。フーリエ変換と逆フーリエ変換を合わせて、フーリエ変換対と称し、$$x(t) \Leftrightarrow X(\omega)$$と表記する。
$x(t)$をフーリエ変換した関数$X(\omega)$は、一般に複素数となるので、実部を$R(\omega)$、虚部を$I(\omega)$として、$$X(\omega) = R(\omega) + j I(\omega) = |X(\omega)| e^{j \phi(\omega)} \\ |X(\omega)| = \sqrt{ R^2(\omega) + I^2(\omega)} \\ \angle{X(\omega)} =\phi(\omega) = \tan^{-1} \frac{I(\omega)}{R(\omega)}$$と表せる。$|X(\omega)|$を信号$x(t)$の振幅スペクトル、$\phi(\omega)$を位相スペクトルという。

フーリエ変換の性質

通常、フーリエ変換$X(\omega)$が存在する十分条件は、$$\int_{-\infty}^{\infty}|x(t)|dt <\infty$$である。つまり、信号$x(t)$は絶対可積分でなければならない。ただし、これは必要条件ではないので、絶対可積分ではない関数、例えば、インパルス関数（$\delta$関数）はフーリエ変換が存在する。
以下にフーリエ変換の主な性質を挙げる。

線形性

$x_1(t) \Leftrightarrow X_1(\omega) \;\;,\;\; x_2(t) \Leftrightarrow X_2(\omega)$のとき、$a\;,\;b$を任意の定数として、$$a x_1(t) + b x_2(t) \Leftrightarrow a X_1(\omega) + b X_2(\omega)$$

対称性

$x(t) \Leftrightarrow X(\omega)$のとき、$X(t) \Leftrightarrow 2 \pi x(-\omega)$

時間軸の推移

$x(t) \Leftrightarrow X(\omega)$のとき、任意の実数$\tau$に対して、$$x(t - \tau) \Leftrightarrow X(\omega)e^{-j \omega \tau}$$

時間微分

$$x(t) = \frac{1}{2 \pi} \int_{-\infty}^{\infty} X(\omega) e^{j \omega t} d \omega$$の両辺を$t$で微分すると、$$\frac{dx(t)}{dt} \Leftrightarrow j \omega X(\omega)$$

時間軸の伸縮

$a$を実定数として、$x(t) \Leftrightarrow X(\omega)$のとき、$$x(at) = \frac{1}{|a|}X\left(\frac{\omega}{a}\right)$$

周波数の推移

$x(t) \Leftrightarrow X(\omega)$のとき、任意の実数$\omega_0$に対して、$$x(t) e^{j \omega_0 t} \Leftrightarrow X( \omega - \omega_0)$$

周波数微分

$$X(\omega) = \int_{-\infty}^{\infty} x(t) e^{-j \omega t} dt$$の両辺を$\omega$で微分すると、$$\frac{dX(\omega)}{d \omega} \Leftrightarrow -j tx(t)$$

特殊関数のフーリエ変換

単位インパルス関数

単位インパルス関数のフーリエ変換を考える。単位インパルス関数は、絶対可積分ではないが、フーリエ変換が存在し得る特殊関数である。単位インパルス関数$\delta(t)$の定義は、次式となる。$$\delta(t)=\begin{cases} \infty \enspace (t=0) \\ 0 \enspace \enspace (t \neq 0)\end{cases} \\ \int_{-\infty}^{\infty} \delta(t) dt =1 $$

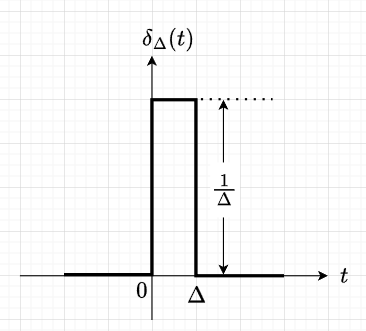
インパルス関数$\delta(t)$の物理的な状態を考えるのは難しいが、工学的には非常に大きな振幅ときわめて小さい幅を持ち、面積が１であるような鋭いパルス状の波形と考えれば良い。また、次の関係が成り立つ。$$\delta(t - \tau)=\begin{cases} \infty \enspace (t=\tau) \\ 0 \enspace \enspace (t \neq \tau)\end{cases} \\ \int_{- \infty}^{\infty} f(t) \delta(t- \tau)dt=f(\tau)$$　図１に示す方形波において、$\Delta \rightarrow 0$とした極限が$\delta(t)$と考えることができる。つまり、$$\delta(t) = \lim_{\Delta \rightarrow 0} \delta_{\Delta}(t)$$である。インパルス関数は特殊関数なので、積分の意味も通常とは異なり、それぞれの式は定義と考えるのが工学的には妥当である。
単位インパルス関数のフーリエ変換は、フーリエ変換の定義式　式(4)を使い、$$\mathcal{F}\{\delta(t)\} = \int_{-\infty}^{\infty} \delta(t) e^{-j \omega t}dt = e^{-j \omega 0}=1$$となる。このように単位インパルス関数のフーリエ変換は１なので、すべての周波数において一様のスペクトルとなることが分かる。

単位ステップ関数

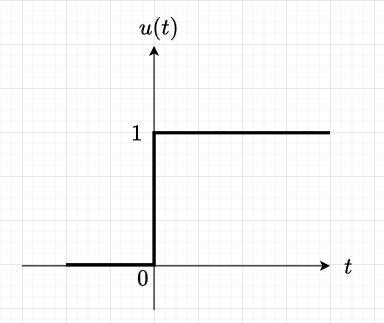
単位ステップ関数は、図２に示す関数で、次の式で定義される。$$u(t) = \begin{cases} 1 \enspace (t \geq 0) \\ 0 \enspace \enspace (t < 0)\end{cases} $$
単位ステップ関数のフーリエ変換は、$$\mathcal{F}\{u(t)\} = \pi \delta(\omega) + \frac{1}{j \omega}$$である。

※単位ステップ関数は、$t=0$において不連続な関数のため、フーリエ変換の導出はやや面倒な議論が必要となるので、下記のサイトを参考にして欲しい。
https://suzumushi0.hatenablog.com/entry/2017/07/02/095303
https://ocw.u-tokyo.ac.jp/lecture_files/engin_01/1/notes/ja/A3-Preliminary.pdf

カテゴリー: ディジタル信号処理