26. 制御仕様
制御仕様について時間領域(ステップ応答)と周波数領域(周波数応答)から考える。
高次制御系のステップ応答特性の評価指標
2次遅れ制御系以上の制御系、例えば、3次制御系のモデルは、2次遅れ制御系×1次遅れ制御系で表せることが多い。詳細は代表極(代表根)と応答特性を参照。
また、モータなどの機構のモデルは、2次遅れ系+高域共振点で表せることが多い。
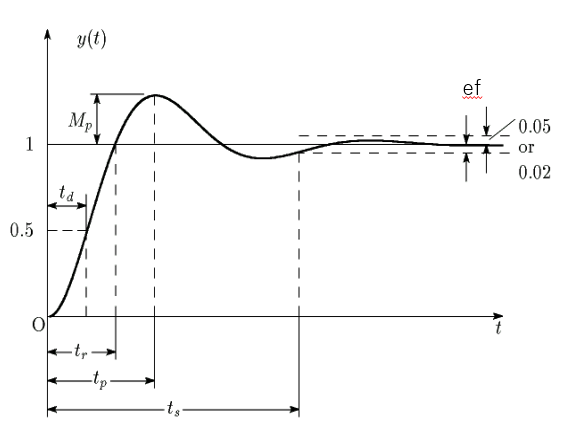
従って、時間領域での特性は、図に示すステップ応答特性を以下の評価指標で評価する。
・遅れ時間(\(t_d\))
・立ち上がり時間(\(t_r\))
・ピーク時間(\(t_p\))
・最大行き過ぎ量(\(M_p\))
・整定時間(\(t_s\))
・定常偏差(\(e_f\))
*速応性の観点からは、\(t_r , t_d , t_p \) をできるだけ小さく。
*減衰性の観点からは、\(M_p , t_s\)をできるだけ小さく。
*定常特性の観点からは、\(e_f\)を小さく。できればゼロにする。
実システムの製作では、制御の目的に応じて具体的な数値を設定する。例えば、目標値到達時間を0.5[s]以下にする、など。
フィードバック制御系の周波数特性と制御仕様
制御の主な目的は、出力を目標値に近づける(偏差をゼロに&出来るだけ速く)ことである。これを閉ループ伝達関数の周波数特性で言い換えると。
1)偏差をゼロに \(\rightarrow\) 利得\(0\)dBで位相\(0^{°}\)。
2)出来るだけ速く \(\rightarrow\) 可能な限り広帯域。
これは、基本的に低域で\(0\)dBの広帯域のLPF(Low Pass Filter)特性となる。
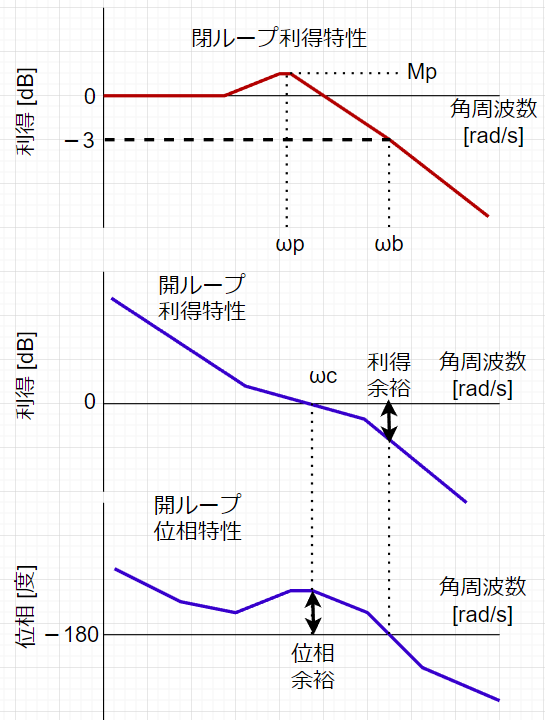
\(\omega_p\):ピーク角周波数(共振角周波数)
\(\omega_b\):遮断角周波数(バンド幅)
\(M_p\):ピーク値(共振値)
閉ループ周波数応答による制御仕様
基本的には、閉ループ周波数応答の利得特性で、利得が\(-3dB\)となるときの角周波数をバンド幅\(\omega _ b\) と定義し、バンド幅\(\omega_b\)はなるべく高くして、速応性を高める。また、\(M_p\)はなるべく小さくして行き過ぎ量を小さくする。しかし、\(M_p\)を小さくすると通常、速応性は悪くなる。
閉ループ周波数応答を基にした制御仕様は、以下となる。
・\(\omega_b\)は制御目的に応じてできるだけ広くとる(高帯域化)。ただし、バンド幅を広くすると、一般的に雑音に弱くなり、エネルギー消費が大きくなる、という問題が生じる。
・ピーク値\(M_p\)はおおむね0.83~3.52dB(1.1~1.5倍)程度が望ましい。(場合によっては0dB)
※開ループ伝達関数\(L(s)=P(s)C(s)\)のベクトル軌跡が\((-1 , j0)\)の近くを通ると\(L(j\omega_0) \approx -1\)なので、\(|1+L(j\omega_0)| \ll 1\)となる。従って、閉ループ伝達関数\(T(j \omega_0)\)では、$$|T(j \omega_0)|=\left|\frac{L(j \omega_0)}{1 + L(j \omega_0)}\right| \gg 1$$となる。従って、\(\omega_0\)近傍で大きなピークを持つことになる。開ループ伝達関数\(L(s)=P(s)C(s)\)のベクトル軌跡が\((-1 , j0)\)の近くを通るということは、不安定に近くなるということで、閉ループ伝達関数で大きなピークを持つということは不安定に近くなっていることに相当する。
開ループ周波数応答による制御仕様
閉ループ周波数応答による指標として、\(M_p\),\(\omega_b\)が挙げられるが、ボード線図を基に制御器\(C(s)\)を設計する場合、開ループ周波数応答を基にした制御仕様の方が分かりやすい場合が多い。これは、閉ループ伝達関数は\(T(s)=\frac{L(s)}{1+L(s)}\)であり、開ループ伝達関数\(L(s)\)で表されることによる。さらに、開ループ伝達関数は\(L(s)=C(s)P(s)\)と、制御対象\(P(s)\)と制御器\(C(s)\)の積で表され、一般的に制御対象\(P(s)\)が既知の基で制御器\(C(s)\)を設計するので、開ループ周波数応答での指標(制御仕様)が必要と考えられる。
開ループ周波数応答を基にした制御仕様は、以下となる。
・利得余裕\(g_m\)は\(10 \sim 20\)dB,位相余裕\(p_m\)は\(40^{°} \sim 60^{°}\)程度が望ましい。(制御目的に応じた時間応答特性も考慮する)
・ゲイン交差角周波数\(\omega_c\) はバンド幅\(\omega_b\)の仕様を満たすように十分大きくとる。


“26. 制御仕様” に対して1件のコメントがあります。
コメントは受け付けていません。